Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерполирование B-сплайнамиСодержание книги
Поиск на нашем сайте
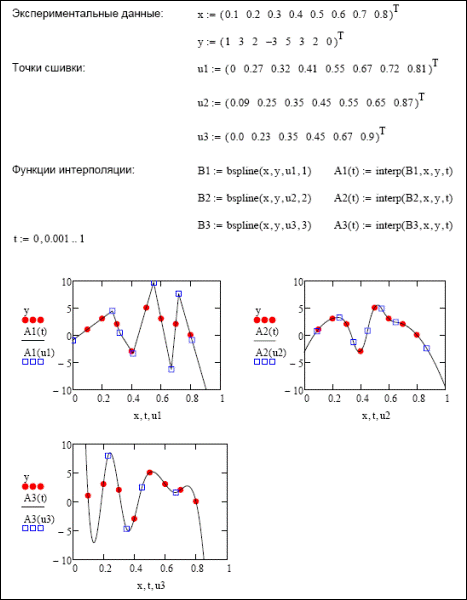
Трудно спорить с тем, что интерполирование экспериментальной зависимости кубическими сплайнами является наиболее эффективным и в то же время простым методом соединения точек гладкой кривой. Однако в некоторых случаях традиционный алгоритм построения сплайна с помощью фрагментов кубических парабол со сшивкой в точках опытных данных может быть непригодным для решения поставленных задач. Если обычный кубический сплайн по тем или иным причинам будет не очень хорошо, как вам покажется, интерполировать данные, то попробуйте использовать возможности приближения B-сплайнами Mathcad. Для построения кривой B-сплайна в программе Mathcad имеется специальная функция bspline(x,y,u,n). В общем, она предназначена для того же, что и остальные функции семейства *spline, а именно: для вычисления матрицы коэффициентов создаваемого сплайна. Основным принципиальным отличием этого типа приближения от простой кубической сплайн-интерполяции является то, что вы самостоятельно можете определить, из фрагментов графиков полиномов какого порядка будет составлена ваша интерполирующая кривая. Сделать это можно, задав соответствующим образом величину параметра n функции bspline(x,y,u,n). Так, если вы хотите приблизить опытную зависимость ломаной линией, то определите n как 1. Если вы считаете, что опытный закон скорее параболический, положите n=2. И, наконец, если вы хотите провести через точки данных кубический сплайн, то n должно быть задано как 3. Вторым отличием, существенно расширяющим возможности B-сплайнов по сравнению с обычными кубическими, является то, что вы самостоятельно произвольным образом можете определять точки, в которых будет произведена сшивка различных фрагментов кривой. Как вы помните, при построении простого кубического сплайна, фрагменты кривых сшивались в самих экспериментальных точках. А это не всегда оправданно, хотя бы в связи с тем, что при этом точки данных очень часто оказываются точками перегиба интерполирующей кривой, что значительно снижает ее корректность в случае использования сплайна в качестве функции прогноза. Иногда бывает гораздо эффективнее сшить элементарные сплайны где-нибудь между экспериментальными точками: при этом результирующая кривая куда лучше отображает реальные процессы (что очень важно в том же моделировании). Чтобы провести сплайн со сшивками в точках, отличных от опытных, вам нужно будет задать вектор, содержащий их координаты по оси X. При этом точки сшивки должны быть рассортированы в порядке возрастания, и значение первой из них должно быть меньше либо равно величине соответствующей координаты левой крайней точки экспериментальной выборки (и соответственно последняя сшивка должна быть расположена правее ее крайней правой точки (или совпадать с нею)). Если вам нужно построить линейный B-сплайн, то сшивок должно быть задано столько же, сколько имеется точек в векторах данных. При приближении зависимости фрагментами парабол, в векторе координат сшивок их должно быть на одну меньше, чем имеется экспериментальных точек. И на целых две точки меньше, чем имеется элементов в выборке, придется определить в рассматриваемом векторе сшивок в том случае, если используемые сплайны - кубические. Кстати, продолжением кубического B-сплайна за пределы области приближаемых данных будет именно кубическая парабола (как вы помните, в зависимости от задания краевых условий, экстраполяция за пределами экспериментальных точек может быть проведена, в общем случае, полиномами 1-3 й степеней). Так как интерполирование с помощью B-сплайнов является технически более непростой задачей, чем построение кривой приближения с использованием обычных функций кубического сплайна, то рассмотрим его более обстоятельно. 1. Сначала нужно организовать опытные данные в виде двух векторов (элементы вектора с координатами по X должны быть отсортированы по возрастанию). Чтобы существовала возможность сравнения, используем для построения сплайна те же данные, что и в предыдущем разделе. 2. Задаем вектор сшивок элементарных сплайнов. Как было указано выше, это следует сделать с учетом порядков приближающих полиномов. Мы же попробуем определить векторы сшивки для сплайнов всех трех типов (сравните количество элементов векторов). 3. Задаем параметры сплайн-кривой с помощью bspline(x,y,u,n), где x и y - векторы опытных данных, u - вектор сшивок, n - порядок используемых полиномов. 4. Задаем функции сплайнов с помощью функции interp(s,x,y,t) 5. Строим графики полученных интерполирующих сплайнов (рис. 33.7). При использовании метода B-сплайнов, для большей корректности на графике стоит отобразить не только экспериментальные точки, но и точки, в которых была произведена сшивка фрагментов приближающих полиномов. Сделать это можно очень просто, внеся в нижний маркер графической области имя вектора сшивок, а в правый - результат вычисления для этого вектора значений функции сплайна. Понять принципиальное различие при использовании B-сплайнов и более простых методов интерполирования можно, сравнив график рис. 5 с рис. 33.7. С первого взгляда в обоих случаях вы, наверное, не заметите особой разницы в ломаных, построенных по двум различным методикам. Однако, изучив их более внимательно, вы увидите, что при применении функции linterp переломы совпадают с точками данных, а при приближении линейным B-сплайном они располагаются в точках сшивок. Аналогичная ситуация наблюдается и при интерполяции гладкими кривыми, правда, при этом нужно говорить не о переломах, а о перегибах. Какой тип интерполяции лучше использовать - на этот вопрос вы должны ответить исходя из собственного опыта и типа решаемой задачи. Однако наиболее общий совет все же можно дать: сначала попробуйте применить функции простого кубического сплайна. В том же случае, если результат его работы вас не устроит, попытайтесь поэкспериментировать с порядком используемых полиномов и точками их сшивок с помощью соответствующих функций B-сплайна.
Рис. 33.7. Решение задачи интерполяции В-сплайнами в MathCAD
Экстраполяция
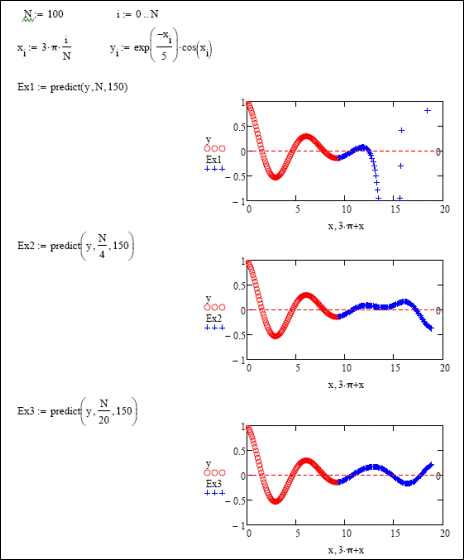
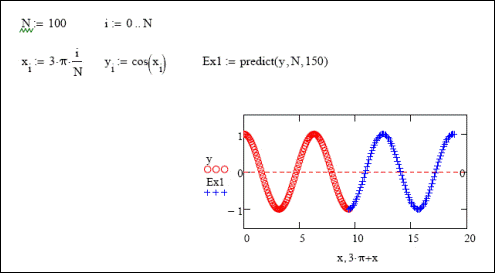
В математике экстраполяцией называется предсказание поведения некоторой зависимости по имеющимся измерениям ее характеристик в определенной, иногда довольно узкой, области. Вообще-то, качественный прогноз такого рода можно дать лишь в случае задания эмпирического закона в виде общей формулы, для чего применяются методы регрессивного анализа. Однако использовать формулы регрессии можно лишь в том случае, если известен математический вид исследуемой зависимости. Во всех остальных случаях приходится применять весьма обобщенные и по этой причине малоэффективные для большинства закономерностей алгоритмы. С полиномиальной экстраполяцией при помощи кубических сплайнов и прямых мы уже познакомились. Однако, вы, наверное, согласитесь, что такой тип предсказания для решения реальных задач вряд ли может быть полезен, так как он более или менее эффективен лишь в том случае, если экстраполируемые данные задаются полиномом невысокой степени. Если же исследуемая зависимость периодическая или склонна к осцилляции, то применение полиномиальной экстраполяции бессмысленно. Некоторые статистические методы позволяют осуществлять более эффективную, чем при использовании полиномов, экстраполяцию разнообразных по форме зависимостей. Принцип их работы основывается на анализе поведения зависимости в нескольких точках, а не только на краях промежутка экспериментальных данных, как в случае применения в качестве прогнозных кривых продолжений сплайнов. В MathCAD функцией, реализующей один из экстраполяционных алгоритмов (linear prediction - линейной экстраполяции) является встроенная функция predict(y,m,n), где: у - вектор эмпирических значений экстраполируемой характеристики по оси ординат. Особенность алгоритма, используемого функцией, заключается в том, что экстраполяцию он делает только на основании у-координат выборки (при этом подразумевается, что шаг по оси абсцисс постоянен). Это вполне оправданно в связи с тем, что экстраполяция обычно проводится для прогноза особенностей поведения кривой, а не определения ее числовых характеристик; m - количество ближайших к правой границе выборки точек, на основании которых проводится экстраполяция; n - количество точек в просчитываемом векторе прогноза. При помощи функции predict можно проводить довольно эффективную экстраполяцию непрерывных, периодических или осциллирующих функций в относительно неширокой области. Например, попробуем предсказать поведение кривой затухающих колебаний. Для этого зададим вектор из у-координат ее 101 точки на промежутке от 0 до 3p. Обязательным условием корректного использования функции predict является то, что шаг изменения переменной при определении вектора данных должен быть постоянным. Очевидно, что простым способом организации такого вектора является использование ранжированных переменных (рис. 8). Далее зададим векторы экстраполяции при помощи функции predict. Чтобы сравнить степень влияния количества анализируемых точек выборки на качество предсказания, определим три экстраполяционных вектора при различных значениях параметра m. Размерность же этих векторов определим, например, как 150 (рис. 33.8). После задания векторов приближений можно построить соответствующие графики. При этом переменная для векторов экстраполяции может быть определена прибавлением к вектору х соответствующей координаты крайнего значения в выборке. В нашем случае это 3p. Такой подход оправдывается тем, что при построении графика мы должны учитывать, что функция predict выдает точки экстраполяции с тем расчетом, что шаг между ними такой же, как и между х - координатами выборки. Внимательно изучив графики на рис. 33.8, вы, наверное, согласитесь, что экстраполяция при помощи функции predict довольно эффективна (с учетом специфики вопроса), однако лишь на небольшом отрезке правее крайней точки выборки. Чем дальше расположен фрагмент приближающей кривой от точек, на основании которых проводится экстраполяция, тем в меньшей степени, скорее всего, он будет соответствовать реальному поведению зависимости.
Рис. 33.8. Использование функции предсказания.
К интересному и неожиданному выводу можно прийти, анализируя влияние количества точек выборки, на основании которых проводится экстраполяция, на точность последней. Казалось бы, чем больше точек обрабатывается, тем точнее должна быть информация о продолжаемой кривой и тем ближе будет график экстраполирующей кривой к реальной зависимости. Однако, глядя на приведенные графики, можно обнаружить, что такой прямой зависимости не существует: в случае обработки всех точек выборки, приближающая кривая быстро возрастает, чего не наблюдается при анализе части экспериментальных точек. Успех экстраполяции зависит от типа исследуемой зависимости. Лучше всего удается предсказание поведения парабол, экспоненциальных кривых и несложных периодических функций. В общем случае - чем сложнее зависимость, тем на более коротком промежутке можно доверять результатам экстраполяции. Такие же простые функции, как синус или косинус, корректно продолжаются функцией predict на сколь угодно широком интервале (рис. 33.9).
Рис. 33.9. Предсказание поведения функции cos(x)
Если в выборке не очень много точек и шаг между ними велик (или при наличии заметной погрешности), пытаться проводить экстраполяцию бессмысленно. Да и, учитывая широкие возможности расчета регрессий в MathCAD, этого и не требуется. Задачей регрессионного анализа является установление параметров экспериментальной зависимости с учетом того, что эмпирические точки получены с некоторой погрешностью. Обычно это делается при помощи расчета минимума тем или иным образом задаваемой функции ошибки. Часто название регрессии упрощают до построения гладкой кривой между точками опытных данных. Однако реальные возможности регрессионного анализа гораздо шире, и без области статистики невозможно представить ни прикладной физики, ни современной техники. Практическая важность регрессии огромна: например, любой корректно построенный график экспериментальной зависимости должен быть задан при ее помощи. Реально задачи регрессии встречаются на практике чаще, чем интерполяции или, тем более, экстраполяции.
Сглаживание данных
Очень важной задачей при обработке экспериментальных данных является устранение шумов - высокочастотных случайных составляющих в сигнале. Алгоритмы, позволяющие решить эту задачу, называются алгоритмами сглаживания (smoothing). Конечно, можно попробовать удалить случайную составляющую из сигнала и с помощью вычисления, например, синусоидальной регрессии или, лучше, регрессии фрагментами полиномов. Однако такой подход не всегда может быть эффективным по той причине, что все-таки регрессия - это очень грубый вычислительный инструмент, и ее использование может уничтожить информативную составляющую в сигнале, особенно если он сложен или быстро изменяется. Немаловажным фактором является и то, что расчет регрессии - это достаточно сложная вычислительная задача, особенно при большом объеме эмпирических данных. По изложенным выше причинам для сглаживания сигнала на практике обычно применяются не регрессивные методы, а более мягкие и простые алгоритмы фильтрации. В Mathcad имеются три встроенные функции, позволяющие произвести сглаживание некоторой выборки данных: 1. medsmooth(y,n), где y - вектор значений сигнала, n - параметр, определяющий количество окон сглаживания, на которое будет разбит интервал при обработке данных (n может быть только нечетным целым числом, строго меньшим, чем количество элементов в выборке). Эта функция реализует популярный алгоритм «бегущих» медиан (running medians). Значение каждой точки заменяется на среднее значение по n точкам данных, окружающих данную (рис. 33.10).
Рис. 33.10. Алгоритм работы функции medsmooth при n=5.
Обязательным условием при ее применении является то, что эмпирические точки должны быть равномерно распределены на промежутке. Из всех встроенных функций сглаживания Mathcad medsmooth является наиболее надежной, однако, и наименее универсальной функцией; 2. ksmooth(x,y,b), где x и y - векторы данных, b - ширина окна сглаживания (этот параметр по величине должен равняться общей величине нескольких промежутков, разделяющих в данной выборке соседние точки). Данная встроенная функция реализует сглаживание на основании алгоритма Гаусса (его описание вы можете прочитать в соответствующей статье справочной системы Mathcad). Эта функция заменяет каждое экспериментальное значение на взвешенное среднее.
При этом веса каждой точки определяются функцией
Лучше всего функция ksmooth подходит для устранения шумов в стационарном сигнале; 3. supsmooth(x,y), где x и y - векторы данных. Осуществляет сглаживание с помощью адаптивного алгоритма (в основе которого лежит метод наименьших квадратов), основанного на анализе взаимного расположения рассматриваемой точки и ближайших к ней (их количество зависит от особенностей поведения графика зависимости). Данная функция лучше всего подходит для сглаживания сложных нестационарных сигналов. Все описанные выше функции возвращают в качестве ответа вектор из такого же количества элементов, как в исходных выборках. Поэтому если эмпирических точек было обработано немного, то при построении графика, для получения корректной кривой, стоит использовать возможности сплайн--интерполяции Mathcad (если же сглаживалась зависимость, образованная более чем 50–-100 точками, то этого, скорее всего, делать не потребуется). Попробуем оценить эффективность функций сглаживания Mathcad. Для этого, используя генератор нормально распределенных случайных чисел, имитируем сигнал со значительным уровнем шума. Построим кривые усреднения при разных величинах окна сглаживания и определим степень влияния этого параметра на качество результата (рис. 33.11 – 33.13). Из приведенных примеров можно заключить, что принципиальным условием успеха при сглаживании сигнала может быть правильный выбор алгоритма (так, например, в случае нашей зависимости метод «бегущих» медиан оказался не на высоте). Кроме того, весьма тщательно нужно относиться и к заданию величины окна сглаживания. Реально алгоритмов, позволяющих решать всевозможные задачи сглаживания и фильтрации, существует гораздо больше, чем встроено в систему Mathcad в виде функций. И любой из них при необходимости может быть весьма просто реализован вами благодаря высокому вычислительному потенциалу системы. Так, можно создать весьма простой и эффективный метода сглаживания, известный как скользящее усреднение. Изучая его, вы оцените, насколько проще в вычислительном плане алгоритмы сглаживания по сравнению с той же регрессией.
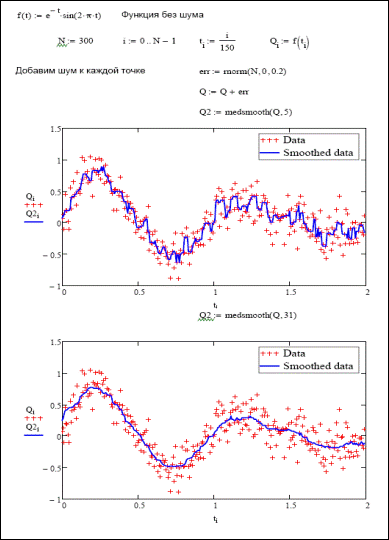
Рис. 33.11. Сглаживание с помощью функции medsmooth. Обратите внимание на влияние ширины окна сглаживания на качество результата
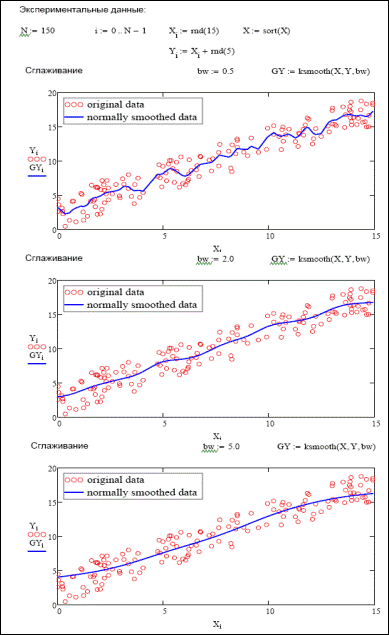
Рис. 33.12. Сглаживание с помощью функции ksmooth.
Регрессия
|
||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 1132; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.158.110 (0.009 с.) |

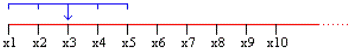
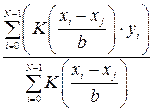 . (33.10)
. (33.10)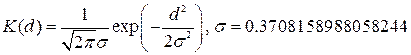 . (33.11)
. (33.11)