
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 10. Основы анализа экспериментальных данныхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
РАЗДЕЛ 10. ОСНОВЫ АНАЛИЗА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ Классификация ошибок
Классификация ошибок измерений. Почему так важно оценить ошибку измерений? Классификация ошибок. Грубые ошибки. Систематические ошибки. Причины возникновения систематических ошибок Случайные ошибки. Анализ и обработка экспериментальных данных
Обзор программного обеспечения для выполнения анализа и обработки экспериментальных данных. Анализ результатов прямых измерений
Анализ результатов измерений случайной величины. Распределение результатов измерений случайной величины. Распределение Гаусса. Среднеквадратичная ошибка отдельного измерения и среднего значения. Косвенные измерения
Ошибки косвенных измерений. Косвенные измерения. Функции случайных величин. Анализ результатов совместных измерений
Анализ результатов совместных измерений. Измерение функциональных зависимостей. Интерполяция и аппроксимация экспериментальных данных. Метод наименьших квадратов. 29. Основные определения. Классификация ошибок измерений
Виды измерений Физическая величина - это характеристика одного из свойств физического объекта (системы, явления или процесса). Значение физической величины представляет собой оценку размера этой величины в виде некоторого числа принятых для нее единиц. Различают истинное значение физической величины, идеально отражающее свойства материального объекта, и действительное - значение, найденное экспериментально. Измерение - это нахождение значения физической величины опытным путем с помощью специальных технических средств. Прямым называется измерение, при котором значение измеряемой величины непосредственно считывается со шкалы прибора, проградуированного в соответствующих единицах измерения. Уравнение прямого измерения имеет вид
где Примерами прямых измерений являются: измерение длины предмета с помощью линейки с миллиметровыми делениями, штангенциркуля или микрометра, измерение силы тока амперметром, напряжения - вольтметром, температуры - термометром и др. Косвенным называется измерение, результат которого определяют на основании прямых измерений величин, связанных с измеряемой величиной известной зависимостью. Уравнение косвенного измерения имеет вид
где Примерами таких измерений являются: определение радиуса шара Совместными называют производимые одновременно измерения двух или нескольких не одноименных величин для нахождения зависимости между ними. Уравнение совместных измерений имеет вид
где Примером совместных измерений может служить нахождение зависимости периода T колебаний математического маятника от его длины l: Моделью объекта измерения называется абстрактный, как правило, идеализированный образ реального объекта. Метод измерений - это совокупность приемов сравнения измеряемой величины с её единицей. Метод измерений осуществляется в соответствии с моделью объекта измерения и доступным набором технических средств.
Классификация погрешностей
Измеряя какую-либо физическую величину, мы не рассчитываем получить ее истинное значение. Поэтому необходимо как-то указать, насколько полученный результат может быть близким к истинному значению, иными словами, указать, какова точность измерения. Воздействие помех на процесс измерения приводит к тому, что результаты измерения всегда отличаются от истинного значения измеряемой величины и по этим результатам определить истинное значение нельзя. Разность между результатом измерения и истинным значением называется истинной погрешностью измерения. В силу того, что истинное значение неизвестно, неизвестной является и истинная погрешность. Учитывая, что ни истинное значение физической величины, ни истинную погрешность в опыте определить невозможно, задачу нахождения истинного значения формулируют как задачу нахождения некоторого приближенного к истинному значения с указанием возможных наибольших отклонений этого приближенного значения от истинного. Найденное в эксперименте значение измеряемой величины, приближенное к истинному, называется оценкой физической величины. Оценка с указанием ее возможного интервала отклонения от истинного значения (доверительного интервала, в котором с определенной степенью достоверности содержится истинное значение) называется результатом измерения. Погрешность измерения включает в себя множество различных составляющих, которые можно классифицировать по различным признакам. В настоящее время классификация погрешностей содержит около 30 видов. По влиянию на результаты измерений их можно разделить на систематические и случайные. По характеру изменения во времени - на статические и динамические. По источникам возникновения - на методические, инструментальные, личные, которые, в свою очередь, могут быть как случайными, так и систематическими. По возможности выявления и исключения из результатов измерения - на выявленные и невыявленные, устранимые и неустранимые, исключенные и неисключенные. По характеру принадлежности (близости) результатов наблюдений к основной совокупности - на грубые и промахи. Невыявленная погрешность всегда неустранима. Выявленная погрешность может быть как устранимой, так и неустранимой. Так, случайная погрешность, а также систематическая погрешность известной величины, но неизвестного знака, имеют определенные численные значения, т. е. относятся к разряду выявленных. Тем не менее, они не могут быть устранены (исключены из результатов), т. е. являются неустранимыми. Дадим определения основных видов погрешностей. Систематическая погрешность - это составляющая погрешности измерения, которая остаётся постоянной или закономерно изменяется при повторных измерениях. Одной из основных задач обработки результатов эксперимента является выявление, оценка величины и, по возможности, устранение всех систематических погрешностей. Изменяющиеся систематические погрешности выявляются легче постоянных. Для выявления постоянной систематической погрешности необходимо выполнить измерения хотя бы двумя различными способами или методами. Обнаруженные и оцененные систематические погрешности исключаются из результатов путем введения поправок. В зависимости от причин возникновения систематические погрешности подразделяют на следующие виды: 1. Погрешности метода или модели, которые обычно называют методическими погрешностями. Например, определение плотности вещества без учета имеющихся в нем примесей, использование формул, не совсем точно описывающих явление, и др. 2. Погрешности воздействия внешних факторов: внешних тепловых, радиационных, гравитационных, электрических и магнитных полей. 3. Погрешности, возникающие из-за неточности действий или личных качеств оператора (экспериментатора), называемые личностными погрешностями. 4. Инструментальные (приборные, аппаратурные) погрешности, обусловленные схемными, конструктивными и технологическими несовершенствами средств измерения, их состоянием в процессе эксплуатации, Например, смещение начала отсчета, неточность градуировки шкалы прибора, использование прибора вне допустимых пределов его эксплуатации, неправильное положение прибору и т. п. За исключением смещения начала отсчета приборные погрешности относятся к разряду неустранимых погрешностей. Есть и другие факторы, которые могут также изменить калибровку чувствительного элемента, приводящие к систематическим ошибкам. В некоторых чувствительных элементах, старение компонентов изменяет реакцию чувствительного элемента и следовательно калибровку. Повреждение или неправильная эксплуатация чувствительных элементов могут также изменить калибровку. Чтобы предотвратить эти систематические ошибки, чувствительные элементы должны периодически повторно калиброваться. Систематические ошибки могут также возникать, если процесс самого измерения модифицирует измеряемую величину. Эта проблема, определяемая как агрессивность воздействия, является ключевой во многих задачах измерения. Взаимодействие между измерением и устройством измерения всегда присутствует; однако, во многих случаях, это воздействие можно свести к незначащему уровню. Например, в электронных системах, энергетическое воздействие измерительного прибора может быть сделано незначительным, используя высокое входное сопротивление. Пример агрессивного воздействия - большой теплый термометр при измерении температуры малого объема холодной жидкости. Тепло переносится от термометра и нагревает жидкость, что приводит к неточному измерению.
Рис. 29. 1. Интерферирующие и модифицирующие воздействия на измерительную систему
Систематические ошибки могут также вноситься в процесса передачи результатов измерения, показанного на рис. 29.2. Если сигнал изменен некоторым способом, измерение будет отличаться от считываемой величины. В механических системах смещение и трение могут модифицировать передачу сигнала. В электрических цепях, сопротивление или затухание могут также модифицировать сигнал, приводя к систематической ошибке. Наконец, систематические ошибки или смещение могут вноситься и наблюдателями при считывании показаний. Пример этой ситуации - ошибка вследствие параллакса. Это погрешность, которая возникает, когда наблюдатель считывает показания под не прямым углом. Поскольку индикаторный указатель расположен выше циферблата, показание будет смещено относительно правильной величины.
Рис. 29.2. Иллюстрация модифицирующего воздействия на измерительную систему
К систематическим ошибкам относятся такие ошибки наблюдений, которые входят в результат по тому или иному закону в зависимости от источника возникновения ошибки. Систематические ошибки подразделяются на постоянные и односторонне действующие. В общем случае систематическая погрешность обусловлена суммарным воздействием перечисленных выше факторов, многие из которых невозможно рассчитать, подавить или выявить в данном эксперименте. Самым простым способом выявления суммарной систематической погрешности было бы сопоставление результатов измерений, полученных с помощью серийного (рабочего) и более точного, образцового приборов. Разность результатов измерений даст суммарную систематическую погрешность, вносимую серийным прибором в результат измерения. Однако такой способ выявления систематической погрешности был бы слишком дорогим. Поэтому на практике различные составляющие систематической погрешности пытаются устранить с помощью экспериментальных или математических приемов путем введения поправок в результаты наблюдений, при условии, что погрешность данного вида по величине и знаку известна. После внесения поправок влияние систематической погрешности данного вида на результат и погрешность измерения устраняется полностью. Если же систематическая погрешность неизвестна, но имеет известные границы изменения, то её учитывают в результате измерения.
Рис. 29.3. Измерительная система с источниками шумов
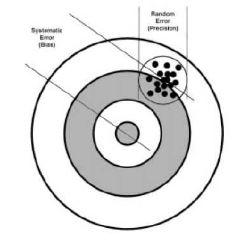
Случайная погрешность - это составляющая погрешности измерения, проявляющаяся в виде непредсказуемых отклонений от истинного значения физической величины, меняющихся от одного наблюдения к другому. Она обусловлена влиянием на результаты измерения множества факторов, воздействие которых на каждое отдельное измерение невозможно учесть или заранее предсказать (рис. 29.3). Такими причинами могут быть перепады напряжения в сети, вибрация установки, изменения атмосферного давления, температуры, электрических, магнитных и радиационных полей, а также ошибки, связанные с действиями самого экспериментатора (неправильное считывание показаний приборов, различная скорость реакции и т. п.). Случайную погрешность нельзя исключить из результатов измерений, однако, пользуясь статистическими методами, можно учесть её влияние на оценку истинного значения измеряемой величины. Грубая погрешность - погрешность измерения, значительно превышающая погрешности большинства результатов наблюдений. Такие погрешности могут возникать вследствие резкого изменения внешних условий эксперимента: внезапного изменения температуры, напряжения в сети и т. п. Грубые погрешности обнаруживают статистическими методами и соответствующие результаты измерений, как не отражающие закономерностей поведения измеряемой величины, исключают из рассмотрения. Промах - это вид грубой погрешности, зависящий от наблюдателя и связанный с неправильным обращением со средствами измерений: неверными отсчетами показаний приборов, описками при записи результатов, невнимательностью экспериментатора, путаницей номеров образцов и т. п. Промахи обнаруживают не статистическими методами и результаты наблюдений, содержащие промахи, как заведомо неправильные, исключают из рассмотрения. Указанные составляющие, как правило, не зависят друг от друга, что допускает их раздельное рассмотрение.
Рис. 29.4. Промахи, систематические и случайные ошибки
Комбинацию промахов, систематических и случайных ошибок может визуализироваться, рассматривая мишень, показанную на рис. 29.4. Систематическая погрешность приводит к группировке выстрелов, смещенных относительно центра мишени (возможно сбит прицел или влияние ветра). Размер группировки определяется источниками случайной ошибки и является критерием точности стрельбы. Полная погрешность измерения, являющаяся суммой указанных составляющих, может быть представлена в абсолютном, относительном или нормированном виде. Абсолютная погрешность - это погрешность измерения, выраженная в единицах измеряемой величины. Наряду с абсолютной погрешностью часто используется термин абсолютное значение погрешности, под которым понимают значение погрешности без учета ее знака. Эти два понятия различны. Относительная погрешность - это погрешность измерения, выраженная отношением абсолютной погрешности к результату измерения. Приведенная погрешность - это погрешность, выраженная отношением абсолютной погрешности средства измерения (приборной погрешности) к некоторой постоянной величине, называемой нормирующим значением и имеющей размерность измеряемой величины. В качестве нормирующего множителя может выступать, например, максимальное значение шкалы прибора (верхний предел показаний прибора). Понятие приведенной погрешности относится только к средствам измерений. Относительная и приведенная погрешности являются безразмерными величинами. Одни составляющие погрешности могут быть устранены из результатов измерений, а другие - нет. Все виды неустранимых погрешностей вносят вклад в полную погрешность измерения, и для ее нахождения должны быть просуммированы по определенным правилам, которые будут рассмотрены в дальнейшем. Когда получен какой-либо экспериментальный результат, он публикуется и становиться общим достоянием. Каждый может пользоваться им, как ему угодно. Одни могут применять его в расчетах для каких-либо практических целей, другие - для проверки теоретических выводов. И в том и в другом случае необходимо знать, достаточно ли точен экспериментальный результат. Если на основании результата делаются какие-нибудь выводы, то важно знать в какой мере можно на них полагаться. Чтобы можно было ответить на подобные вопросы экспериментатор и обязан указывать ошибку измерения. Некоторые могут подумать, что всякий эксперимент следует проводить как можно более точно, но такой подход был бы нереален. Поэтому важно планировать и проводить эксперимент так, чтобы точность окончательного результата соответствовала его цели. Мы видим, что понятие ошибки измерения играет далеко не второстепенную роль в эксперименте. Наоборот, оно имеет прямое отношение к таким вопросам, как цель эксперимента, его метод и значимость его результатов. Приведу ряд примеров, когда недостаточное внимание к надлежащей обработке полученных экспериментальных данных приводило даже известных ученых к невероятным просчетам. Холодный ядерный синтез. В 1989 два исследователя из Университета г. Юта (США), Стенли Понс и Мартин Флейшман, объявили, что им удалось осуществить ядерный синтез на установке, состоящей и паладиевых цилиндров, погруженных в сосуд с дейтерием. Ученые установили, что их прибор испускает нейтроны и гамма лучи, что является свидетельством ядерной, а не химической реакции. Это заявление вызвало огромное возбуждение в научном мире и прессе. Говорилось о начале новой эры дешевой и неограниченной энергии для всего человечества. Однако эти утверждения оказались неверными: холодного ядерного синтеза в этой форме не существует. Наряду с другими экспериментальными погрешностями, Понс и Флейшман пренебрегли простой процедурой оценки ошибок экспериментальных данных. Зафиксированные ими результаты не превышали обычного фона излучения в Университете. Диета. В начале семидесятых исследователи сообщали о том, что диета, богатая клетчаткой, уменьшает вероятность заболевания раком. В результате множество людей стали использовать эту диету. В январе 2000 в Английском Медицинском Журнале были опубликованы результаты тщательных исследований, которые показали, что такая диета не оказывает нужного эффекта. Причина неверных выводов ранних исследований состояла в том, что были использованы очень небольшие выборки и результаты анализа были статистически незначимы. Другими словами, ошибки результатов, полученных на двух группах пациентов, использующих и не использующих диету, были велики, что в пределах этих ошибок результаты можно считать одинаковыми. Очень странная аппроксимация. Два наиболее престижных научных журнала мира - Nature и Science. В одном из них был опубликован рисунок (рис. 2.5) и подпись к нему из статьи Devid W. Rubik (Science 201 (1978), 1030).
Рис. 29.5. Очень странная аппроксимация
В подписи ясно сказано, что кривая - "`наилучшая аппроксимация"' экспериментальных данных. Как вы видите, кривая никак не отражает действительного вида данных. Данные скорее напоминают некую птицу с клювом в верхнем левом углу рисунка и смотрящую влево.
MathCAD
MathCAD является представителем нового поколения программных средств и предназначен для инженерных и математических расчетов. Он чрезвычайно прост в использовании и лёгок в освоении. Его интерфейс настолько удобно сделан, что пользователь работает с рабочим листом программы, как с листом бумаги, где он пишет формулы и математические выражения в их привычной нотации. Mathcad может выполнять вычисления любой степени сложности и ограничен лишь техническими возможностями вашей техники. Помимо численных расчетов, он может выполнять и символьные вычисления (здесь это называется "символьная математика"). Имеются обширные графические возможности. Помимо традиционных типов графиков можно строить поверхности, линии уровня и векторные поля. Очень интересное и полезное изобретение разработчиков заключается в создании электронной книги, она называется "Центр ресурсов". В книге помещены многочисленные примеры решения типичных задач, причём их можно не только просматривать, но и переносить на свой рабочий лист обычной операцией копирования или буксировкой. Таких электронных книг по различным областям науки и техники существует великое множество и их можно извлекать с серверов Internet.
Рис. 30.2. Решение задачи сплайн – интерполяции экспериментальных данных в Mathcad
Mathcad Explorer. При расчетах и чтении MathCAD документов можно использовать бесплатную программу MathCAD Explorer, но эта программа не позволяет сохранить результаты расчетов. Последнюю версию программы вы можете скачать или с сайта MathSoft, или с образовательного математического сайте http://www.Exponenta.ru. Ниже приведены еще две более специализированные программы, предназначенные для графического представления и статистической обработки различных данных. Программы легко интегрируются с MathCAD и могут использоваться с ним совместно дополняя друг друга. S-Plus - мощная программа для статистической обработки и графического представления результатов измерений. Программа хорошо интегрируется с MathCAD и позволяет получать графическое представление расчетов в виде, готовом для публикации в отчете или дипломном проекте. Axum (по существу, облегченная версия S-Plus). Демонстрационные версии всех программ можно скачать на сайте MathSoft (http://www.mathsoft.com).
Matlab - Scilab - Octave
Системы компьютерной математики (СКМ) сегодня стали важнейшим рабочим инструментом во многих фундаментальных и прикладных науках. Их использование существенно облегчает исследователю жизнь, а зачастую вообще является единственным способом получения каких-либо значимых результатов. Однако для большинства отечественных пользователей коммерческие СКМ высшего класса (MathCAD, Mathematica, Maple и др.) слишком дороги. Разумным и фактически безальтернативным выходом представляется бесплатное ПО, и оказывается, в нем также встречаются весьма качественные разработки, одной из которых является Scilab. Пакет Scilab является свободно распространяемой (вместе с исходными кодами) системой компьютерной математики. До недавнего времени он разрабатывался исследовательскими институтами INRIA и ENPC (оба находятся во Франции), а с мая 2003 г. поддержку продукта взял на себя специально созданный для этой цели Scilab Consortium, с Web-узла которого (http://scilabsoft.inria.fr/) можно загрузить последнюю версию программы и полный комплект документации (на момент подготовки материала была доступна версия 4.0). Scilab выпускается для операционных систем Windows (любая 32-разрядная версия), наиболее популярных Unix/Linux и не нуждается в больших системных ресурсах: инсталляционный модуль имеет размер до 20 MB, а для установки требуется немногим более 40 MB. Пакет не случайно имеет название, созвучное с Matlab -- одной из наиболее мощных коммерческих СКМ. У обоих приложений немало общего -- от интерфейса и принципа взаимодействия с пользователем через командную строку до синтаксиса языка. Таким образом, Scilab можно рассматривать как облегченный вариант Matlab, который, впрочем, сохраняет основные возможности последнего. Scilab является типичным командным интерпретатором и структурно состоит из интерпретирующей системы, принимающей команды пользователя и возвращающей результаты, и двух библиотек: собственных функций и дополнительных -- на языках С и Fortran. Хотя Scilab является бесплатным продуктом, его вычислительные возможности, обеспеченные приблизительно тысячью встроенных функций, вполне соответствуют СКМ профессионального уровня. Функции системы, относящиеся к некоторым прикладным областям математики и техники, собраны в дополнительные пакеты расширений (так называемые toolboxes). Одни из них применяются достаточно широко (как, скажем, методы численного решения краевых задач для систем дифференциальных уравнений, линейное и квадратичное программирование), другие имеют узкую специфическую направленность. Из последних назовем пакеты для цифровой обработки сигналов, анализа динамических систем, оптимизации со специальными ограничениями. Scilab является надежной и мощной платформы для создания недорогих, но вполне конкурентоспособных решений в области обработки данных, численной реализации алгоритмов и визуализации. Поэтому если перед вами стоят подобные задачи, стоит обратить пристальное внимание на эту неординарную и доступную вычислительную систему.
Рис. 30.3. Рабочее окно, окно встроенного редактора программ и графическое окно Scilab.
Octave - интерактивная программная система с открытым исходным кодом для числовых вычислений и построения графиков. Она предназначена в основном для матричных вычислений: решения систем уравнений, вычисления собственных векторов и собственных значений и так далее. Во многих реальных технических задачах данные могут быть представлены как матрицы и векторы, и решение этих задач сводится к этим формам решения. Кроме того, Octave может представлять данные различным образом, а также имеет свой собственный язык программирования, который позволяет расширять систему. Об Octave можно говорить как об очень мощном, программируемом, графическом калькуляторе. Octave облегчит Вам решение широкого круга числовых задач и оставит больше времени на эксперимент и обдумывание более широкой проблеме. Ценность Octave увеличивается еще и в связи с тем, что синтаксисом она совместима с MATLAB, который обычно используется в промышленности и науке. Octave разработана для решения математических задач численно. Это означает, что Octave может не всегда давать точное решение задачи, и ее не должно путать с программами типа Mathematica или Maple, которые дают символьные решения, делая алгебраические манипуляции. Это не означает, что Octave лучше или хуже - она используется для решения своего круга задач. Самые реальные математические проблемы (особенно технические!) не имеют четких символьных решений.
Рис. 30.4. Программа Octave.
Octave и MATLAB широко используются инженерами и учеными и в промышленности и в науке для того, чтобы выполнять числовые вычисления, и для того, чтобы разработывать и проверять математические алгоритмы. Например, NASA использует ее для разработки космических кораблей; Jaguar Racing - чтобы отображать и анализировать данные, переданные от автомобилей Formula 1; Sheffield University - для разработки программного обеспечения для распознаваия злокачественных клеток.
Построение графиков
Для графического представления результатов измерений и расчетов можно использовать все вышеприведенные программы, но есть специализированные программы, которые обеспечивают создание графиков очень высокого качества и позволяют делать их по всем требованиям, которые предъявляются к публикациям в журналах или к оформлению курсовых и дипломных проектов. Grapher, Origin, SigmaPlot, Gnuplot и т.д.
Sigma Plot
Sigma Plot (последняя версия 9) - наиболее удобная на мой взгляд программа, позволяющая не только строить разнообразные графики, но и производить анализ экспериментальных данных.
Рис. 30.5. Программа построения графиков и обработки данных SigmaPlot
Origin
Похожими возможностями обладает и еще одна широко распространенная в научной и инженерной среде программа – Origin.
Рис. 30.6. Программа построения графиков и обработки данных Origin
Gnuplot
Gnuplot - удобная и свободно распространяемая программа. Особенно популярна программа в университетской и академической среде. Программа консольная. Для построения графика необходимо создать обычный текстовый файл содержащий команды. Пример командного файла *.plt, набранного во встроенном редакторе Gnuplot или в любом текстовом редакторе: set nokey set terminal postscript enhanced mono set output "F_2.eps" set size 0.7,1 set origin 0,0 set multiplot set pointsize 0.5 set origin 0,0 set size 0.7,1 set yrange [50:120] set xrange [100:375] set label "a" at 120,115 set xlabel "T, K" set ylabel "C_{p}, J/mol{/Symbol \327}K" plot 'Cp_BTZ35.dat'using 1:2 with points 6, 'Latt_BTZ35.dat'using 1:2 with lines 1 set origin 0.25,0.1 set size 0.4,0.4 set arrow from 100,0 to 370,0 nohead set xrange [100:370] set label "b" at 130,1.5 set xlabel "T, K" set yrange [-0.5:2.0] set ylabel "{/Symbol D}C_{p}, J/mol{\264}K" plot 'btz35.txt' with points 6 unset multiplot
Результат работы программы показан на рис. 30.8.
Рис. 30.7. Программа Gnuplot
Рис. 30.8. Результат работы программы Gnuplot
Работа с текстом
MS Word
Microsoft Word - (сейчас доступен Word 2007) фактически все тексты набиваются в нем. Вряд ли имеет смысл рассказывать о его достоинствах. Если вам необходимо набирать много математики, лучше всего заменить встроенную программу - редактор математических формул на MathType - более мощную и удобную программу.
OpenOffice.org
Альтернативой Microsoft Word может служить все более набирающая популярность свободно распространяемая программ OpenOffice.org. OpenOffice.org - это свободный набор офисных программ, в состав которого входят следующие компоненты: - Writer (текстовый процессор и редактор HTML). - Calc (электронные таблицы). - Draw (графический редактор). - Impress (система презентаций). - Редактор формул Match. - Модуль доступа к данным. OpenOffice.org является полноценным офисным пакетом, не уступающим по своим возможностям таким популярным проприетарным программам, как MS Office. Он содержит компоненты для работы с текстом, электронными таблицами, работает с базами данных, обрабатывает графику, создает сложные документы интернет-публикаций. Разработчики OpenOffice.org, внедряя передовые технологии обработки документов, старались максимально облегчить работу обычным пользователям. Поэтому при первом знакомстве вы попадаете в привычную среду, знакомую по приложениям MS, и можете сразу начать работу. Переучиваться не нужно; навыков работы с MS Office вполне достаточно. Если у вас есть книги по MS Office, то они подойдут и для первого знакомства с OpenOffice.org - основные приемы работы чрезвычайно похожи. Начав использовать OpenOffice.org, вы можете по-прежнему работать со всеми файлами, которые подготовили ранее в среде MS Office, и спокойно обмениваться документами c пользователями других программ. OpenOffice.org читает и сохраняет документы в большинстве популярных форматов. К ним относятся файлы MS Word, Excel, PowerPoint, RTF, html, xhtml, DocBook, простые текстовые файлы в различных кодировках. Кроме того, начиная с версии 1.1 OpenOffice.org, позволит экспортировать сложные документы с иллюстрациями и графиками в популярном формате pdf. Система презентаций Impress позволяет экспортировать презентации в популярный формат Macromedia Flash (.swf). OpenOffice.org содержит все необходимые компоненты для создания сложных систем. Он поддерживает шаблоны, умеет работать с базами данных, содержит собственный язык программирования
Рис. 30.9. Рабочее окно текстового редактора Write из пакета OpenOffice
30.4.3. Latex (Miktex (ProTeX) +TeXnicCenter)
TeX - система для верстки текстов с формулами (название, американский математик и программист Дональд Кнут, придумал от греческих "Технология" и "Искусство", поэтому последняя буква читается как русское Х). Преимущества: - наивысшее типографское качество при печати; - сколь угодно сложные математические формулы; - работает на всех существующих компьютерных платформах; - гибкие средства для работы с логической структурой текста; -.... Недостатки: - не является системой типа WYSIWYG; - результат нужно печатать на лазерном или РоstScript принтере; -... Поэтому при выборе системы подготовки текста нужно все взвесить. В каких-то случаях можно обойтись и Microsoft Word. Необходимость использования TeXa можно обосновать тем, что он: - язык международного обмена по математике и физике (большинство научных издательств принимают тексты в печать только в этом формате); - средство обмена в рамках Internet/Intranet (система хранения и доступа к статьям, отчетам и т.д. в формате HTML).
Рис.30.10. Результат работы LATEX.
Кусок текста, набранный в любом текстовом редакторе, сохраняется в файле с расширением *.tex, например file.tex
\documentclass [12pt]{article} \usepackage {graphicx} \usepackage[cp1251]{inputenc} \usepackage[russianb]{babel} \usepackage{a4,color} \usepackage{verbatim} \usepackage{amsmath} \usepackage{srctex} \begin{document} Разница коэффициентов линейного теплового расширения двух различных материалов может быть использована при конструировании термометров. Эта разность дается уравнением \[ \Delta l = l(1+\alpha _1\Delta T)-l(1+\alpha _2\Delta T) = l(\alpha _1-\alpha _2)|Delta T \] где $l$ - длина сенсора, $\alpha _1$ и $\alpha _2$ - коэффициенты линейного теплового расширения двух материалов, $\Delta T$ - изменение температуры.
\begin{figure} \centering \includegraphics[width=0.90\textwidth]{dil1.ps} \caption{Принцип действия дилатометрического термометра} \label{fig:dil1} \end{figure}
\end{document} Результат работы LaTeX после введения последовательности команд latex file.tex в командной строке показан на рис.30.10. Но лучше работать в специальном TeX-редакторе — TeXnicCenter (Windows) или Kile (Linux)
Ошибки косвенных измерений
В большинстве экспериментов интересующая нас величина непосредственно не измеряется. Вместо этого мы измеряем некоторые другие величины Например, измерить плотность | ||
|
| Поделиться: |

 (29.1)
(29.1)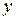 - значение измеряемой величины,
- значение измеряемой величины,  - цена деления шкалы прибора в единицах измеряемой величины,
- цена деления шкалы прибора в единицах измеряемой величины,  - отсчет по индикаторному устройству в делениях шкалы.
- отсчет по индикаторному устройству в делениях шкалы.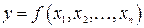 , (29.2)
, (29.2)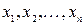 , измеряемых прямым методом. Можно сказать, что косвенное измерение - это измерение, результат которого рассчитывается по формуле.
, измеряемых прямым методом. Можно сказать, что косвенное измерение - это измерение, результат которого рассчитывается по формуле. , площади его поверхности
, площади его поверхности  или объёма
или объёма  по прямо измеренной величине - диаметру шара
по прямо измеренной величине - диаметру шара 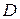 .
.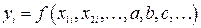 , (29.3)
, (29.3) - значения величин, измеренных одновременно (прямо или косвенно) в i -й измерительной операции; a, b, c,... - неизвестные искомые величины. Если число уравнений превышает число неизвестных, то эти уравнения в отличие от обычной системы уравнений называют условными. Для её решения используют метод наименьших квадратов.
- значения величин, измеренных одновременно (прямо или косвенно) в i -й измерительной операции; a, b, c,... - неизвестные искомые величины. Если число уравнений превышает число неизвестных, то эти уравнения в отличие от обычной системы уравнений называют условными. Для её решения используют метод наименьших квадратов.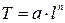 , где a и n - неизвестные параметры, определяемые методом наименьших квадратов.
, где a и n - неизвестные параметры, определяемые методом наименьших квадратов.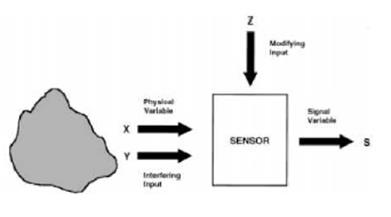












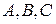 и т.д., а затем вычисляем величину
и т.д., а затем вычисляем величину  , которая является известной функцией первичных величин.
, которая является известной функцией первичных величин. некоторого материала можно, измеряя массу прямоугольного бруска
некоторого материала можно, измеряя массу прямоугольного бруска 


