
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Среднеквадратичная ошибка среднего.Содержание книги
Поиск на нашем сайте
Допустим, что
При этом число
Требуется определить, какова ошибка в величине Ошибку
где
Теперь представим себе, что данные наблюдаются сериями по Величины
Следовательно
Усредним это выражение по всем сериям. Среднее величины
По определению
Тогда равенство можно переписать в виде
т.е. среднеквадратичная ошибка среднего из Величина
Хотя соотношение (31.21) имеет важное значение, но оно не позволяет нам вычислить
но Для
В отличие от ошибки остаток - известная величина. Обозначим среднеквадратичное значение
Величина
Поэтому
Все это относится к одной серии измерений. Усреднив, как и раньше, последнее равенство по большому числу серий, получим
и
Величина
Таким образом, мы приблизительно выразили величину
|
|||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 366; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.209.122 (0.006 с.) |

 последовательных измерений некоторой величины дали значения
последовательных измерений некоторой величины дали значения . (31.13)
. (31.13) . (31.14)
. (31.14) .
. -го измерения мы напишем в виде
-го измерения мы напишем в виде , (31.15)
, (31.15) - истинное значение измеряемой величины, которое, конечно, неизвестно. Тогда ошибка среднего дается выражением
- истинное значение измеряемой величины, которое, конечно, неизвестно. Тогда ошибка среднего дается выражением . (31.16)
. (31.16) . В каждой серии имеется свое среднее значение, и совокупность всех таких средних характеризуется своим распределением со среднеквадратичным отклонением
. В каждой серии имеется свое среднее значение, и совокупность всех таких средних характеризуется своим распределением со среднеквадратичным отклонением  . В реальном эксперименте мы, конечно, имеем дело лишь с одной серией из
. В реальном эксперименте мы, конечно, имеем дело лишь с одной серией из  . (31.17)
. (31.17) . (31.18)
. (31.18) есть
есть 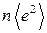 . Среднее каждого члена двойной суммы равно нулю, поскольку ошибки
. Среднее каждого члена двойной суммы равно нулю, поскольку ошибки  и
и  независимы и в среднем равны нулю. Итак, мы получаем следующее равенство
независимы и в среднем равны нулю. Итак, мы получаем следующее равенство . (31.19)
. (31.19) . (31.20)
. (31.20)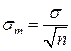 , (31.21)
, (31.21)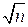 меньше среднеквадратичной ошибки отдельного измерения.
меньше среднеквадратичной ошибки отдельного измерения. , повторять много раз измерение одной и той же величины оказывается не очень выгодным. Лучше попытаться уменьшить
, повторять много раз измерение одной и той же величины оказывается не очень выгодным. Лучше попытаться уменьшить  , (31.22)
, (31.22) . (31.23)
. (31.23) .
. . (31.24)
. (31.24) . (31.25)
. (31.25) . (31.26)
. (31.26) , (31.27)
, (31.27) (31.28)
(31.28) . (31.29)
. (31.29) нам не известна. В качестве ее наилучшей оценки выберем
нам не известна. В качестве ее наилучшей оценки выберем  . Подставляя эту величину в формулу и, извлекая квадратный корень, получаем
. Подставляя эту величину в формулу и, извлекая квадратный корень, получаем (31.30)
(31.30)


