
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка точности измерений углов и превышенийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ПО НЕВЯЗКАМ В ПОЛИГОНАХ И ХОДАХ
Невязки в сумме углов теодолитных полигонов (ходов) являются погрешностями этих сумм, т.е.
где N – количество невязок; P – вес отдельного значения невязки. Если вес вычислять по формуле
где n – количество углов хода, то величина СКП единицы веса
Для контроля вычисляют
Невязки в суммах превышений нивелирных полигонов (ходов) являются погрешностями этих сумм. Для вычисления СКП превышения по ходу длиной в 1 км используют формулу
где
Контрольная формула
При значительных углах наклона местности, когда число станций на 1 км периметра полигона превышает 25, для вычисления СКП превышения по ходу длиной в 1 км используют формулу
где n – число станций (штативов) в полигоне (ходе). Веса невязок в этом случае вычисляют по формуле
Контрольная формула
Решение задач Пример 12. Произвести оценку точности нивелирования по невязкам полигонов, указанным в таблице.
[ n ]=378 В данном случае СКП единицы веса есть СКП превышения на 1 станцию хода
Контроль: Считая, что в среднем на 1 км хода приходится 10 станций, получим СКП превышения на 1 км по формуле
Задача 26. В таблице приведены невязки в полигонах геометрического нивелирования и периметры полигонов. Оценить точность нивелирования.
Задача 27. Произвести оценку точности измерения горизонтальных углов в замкнутом теодолитном ходе по невязкам в полигонах.
Задача 28. По невязкам в треугольниках сети триангуляции произвести оценку точности угловых измерений.
ОЦЕНКА НАДЕЖНОСТИ ОПРЕДЕЛЕНИЯ СРЕДНЕАРИФМЕТИЧЕСКОГО С ИСПОЛЬЗОВАНИЕМ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ Доверительным называется интервал
где n – объем выборки;
Пример 13. Построить доверительный интервал для математического ожидания случайной величины X при
В качестве исходного положения примем
По табл. 3 (см. приложение) для
Доверительный интервал будет
Задача 29. Произведено 16 измерений теодолитом 4Т30П горизонтального угла полным приемом, со СКП 0,5'. Найдите доверительный интервал погрешностей теодолита с надежностью Задача 30. Случайная величина X имеет нормальное распределение с известным СКП Задача 31. Решить задачи 13, 14 и 15 с использованием доверительных интервалов.
СПРАВОЧНЫЕ СВЕДЕНИЯ
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 692; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.134.196 (0.006 с.) |

 . Поэтому для оценки точности измерений по невязкам используется формула
. Поэтому для оценки точности измерений по невязкам используется формула , (3.19)
, (3.19) – невязки;
– невязки; ; (3.20)
; (3.20) будет равна СКП измерения одного угла
будет равна СКП измерения одного угла . (3.21)
. (3.21) по другой формуле
по другой формуле . (3.22)
. (3.22)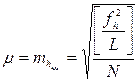 , (3.23)
, (3.23) – невязки, веса которых
– невязки, веса которых (3.24)
(3.24) – периметры полигонов (ходов) в км.
– периметры полигонов (ходов) в км. . (3.25)
. (3.25) , (3.26)
, (3.26)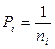 . (3.27)
. (3.27) . (3.28)
. (3.28) , мм
, мм


 =2899
=2899  = 49
= 49 .
.
 .
.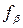
 , который с заданной надежностью
, который с заданной надежностью  покрывает оцениваемый параметр. Для оценки математического ожидания
покрывает оцениваемый параметр. Для оценки математического ожидания 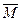 случайной величины X, распределенной по нормальному закону, при известной дисперсии
случайной величины X, распределенной по нормальному закону, при известной дисперсии  служит доверительный интервал
служит доверительный интервал , (3.29)
, (3.29) – точность оценки;
– точность оценки; – аргумент функции Лапласа;
– аргумент функции Лапласа; и
и  – границы доверительного интервала.
– границы доверительного интервала. Имеем:
Имеем:

 , где
, где  - предельная величина погрешности измерения.
- предельная величина погрешности измерения.
 и
и  находим
находим  , откуда
, откуда
 .
. . Найдите доверительные интервалы для оценки неизвестного математического ожидания по выборочным средним
. Найдите доверительные интервалы для оценки неизвестного математического ожидания по выборочным средним  , если объем выборки n =25 и задана надежность оценки
, если объем выборки n =25 и задана надежность оценки 


