
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие положительной скалярной величины и ее измеренияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Рассмотрим два высказывания, в которых используется слово «длина»: 1) Многие окружающие нас предметы имеют длину. 2) Стол имеет длину. В первом предложении утверждается, что длиной обладают объекты некоторого класса. Во втором речь идет о том, что длиной обладает конкретный объект из этого класса. Обобщая, можно сказать, что термин «длина» употребляется для обозначения свойства, либо класса объектов (предметы имеют длину), либо конкретного объекта из этого класса (стол имеет длину). Но чем это свойство отличается от других свойств объектов этого класса? Так, например, стол может иметь не только длину, но и быть изготовленным из дерева или металла; столы могут иметь разную форму. О длине можно сказать, что разные столы обладают этим свойством вразной степени (один стол может быть длиннее или короче другого),чего; не скажешь о форме - один стол не может быть «прямоугольнее» другого. Таким образом, свойство «иметь длину» - особое свойство объектов, оно проявляется тогда, когда объекты сравнивают по их протяженности (по длине). В процессе сравнения устанавливают, что либо дваобъекта имеют одну и ту же длину, либо длина одного меньше (больше) длины другого. Аналогично можно рассматривать и другие известныевеличины:площадь, массу, время и т.д. Они представляют собой особые свойства окружающих нас предметов и явлений и проявляются при сравнении предметов и явлений по этому свойству, причем каждая величина связана с определенным способом сравнения. Величины, которые выражают одно и то же свойство объектов, называются величинами одного рода или однородными величинами. Например, длина стола и длина комнаты - это величины одного рода. Напомним основные положения, связанные с однородными величинами. 1. Для величин одного рода имеют место отношения «равно», «меньше» и «больше», и для любых величин А и В справедливо одно и только одно из отношений: А < В, А = В, А > В. Например, мы говорим, что длина гипотенузы прямоугольного треугольника больше, чем длина любого катета этого треугольника, масса яблока меньше массы арбуза, а длины противоположных сторон прямоугольника равны. 2. Отношение «меньше» для однородных величин транзитивно: если А < В и В < С, то А < С. Так, если площадь треугольника F1 меньше площади треугольника F2 площадь треугольника F2 меньше площади треугольника F3, то площадь треугольника F1 меньше площади треугольника F3. 3. Величины одного рода можно складывать, в результате сложения получается величина того же рода. Иными словами, для любых двух величин А и В однозначно определяется величина С = А + В, которую называют суммой величин А и В. Сложение величин коммутативно и ассоциативно. Например, если А - масса арбуза, а В - масса дыни, то С = А + В - это масса арбуза и дыни. Очевидно, что А +В = В + А и (А + В) + С = А + (В + С). 4. Величины одного рода можно вычитать, получая в результате величину того же рода. Определяют вычитание через сложение. Разностью величин А и В называется такая величина С = А - В, что А = В + С. Разность величин А и В существует тогда и только тогда, когда А>В. Например, если А - длина отрезка а, В - длина отрезкаb, то С = А - В - это длина отрезка с.
Например, если А - время, отводимое на один урок, то умножив А на число х = 3, получим величину В = 3 ´ А - время, за которое пройдет 3 урока. 5. Величины одного рода можно делить, получая в результате число. Определяют деление через умножение величины на число. Частным величин А и В называется такое положительное действительное число х = А: В, что А = х ´В. Так, если А - длина отрезкаа, В -длина отрезка b (рис. 2) и отрезок а состоит из 4 отрезков, равных b, то А: В = 4 поскольку А = 4× В. Величины, как свойства объектов, обладают еще одной особенностью - их можно оценивать количественно. Для этого величину надо измерить. Чтобы осуществитьизмерение, из данного рода величин выбирают величину, которуюназывают единицей измерения. Мы будем обозначать ее буквой Е. Если задана величина А и выбрана единица величины Е (того же рода), то измерить величину А - это значит найти такое положительное действительное число х, что А = х × Е. Число х называется численным значением величины А при единице величины Е. Оно показывает, во сколько раз величина А больше (или меньше) величины Е принятой за единицу измерения. Если А = х × Е, то число х называют также мерой величины А единице Е и Х = mЕ (А)
В практической деятельности при измерении величин люди пользуются стандартными единицами величин: так, длину измеряют вметрах, сантиметрахи т.д. Результат измерения записывают в таком виде: 2,7 кг; 13 см; 16 с. Исходя из понятия измерения, данного выше, эти записи можно рассматривать как произведение числа и единицы величины. Например, 2,7 кг = 2,7 × кг; 13 см = 13 × см; 16 с = 16 × с. Используя это представление, можно обосновать процесспереходаот одной единицы величины к другой. Пусть, например, требуется выразить Величина, которая определяется одним численнымзначением,называется с калярной величиной.
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 859; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.01 с.) |

 ч в минутах. Так как
ч в минутах. Так как  ч =
ч =  × ч и час = 60 мин, то
× ч и час = 60 мин, то 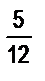 ч =
ч = 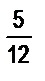 × 60 × мин = (
× 60 × мин = ( × 60) мин = 25 мин.
× 60) мин = 25 мин.


