
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отрицание высказываний и высказывательных формСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть предложение А – высказывание. Если перед сказуемым данного предложения поставить частицу «не» либо перед всем предложением поставить слова «неверно, что», то получится новое предложение, которое называется отрицанием данного и обозначается Определение. Отрицанием высказывания А называется высказывание Таблица истинности отрицания имеет вид:
Из данного определения следует, что предложение и его отрицание не могут быть ни одновременно истинны, ни одновременно ложны. Построим, например, отрицание ложного высказывания «число 28 делится на 9»: а) Число 28 не делится на 9. б) Неверно, что число 28 делится 9. Высказывания, которые мы получили, истинные. Значит, отрицание данного предложения построено правильно. Рассмотрим теперь правила построения отрицания конъюнкции и дизъюнкции высказываний. Если перед всем составным высказыванием поставить слова «неверно, что», то, безусловно, получим его отрицание. А как быть с частицей «не»? Можно ли поставить ее перед сказуемым составного предложения и получить его отрицание? Возьмем, например, высказывание «число 28 делится на 9 и на 4». Оно ложное, так как представляет собой конъюнкцию двух высказываний, одно из которых ложно. Поставив перед сказуемым этого высказывания частицу «не», получим конъюнкцию «число 28 не делится на 9 и на 4», в которой одно из предложений «число 28 не делится на 4» – ложное и, значит, ложно построенное с помощью частицы «не» предложение. Поэтому оно не является отрицанием высказывания «число 28 делится на 9 и на 4». Можно доказать, что отрицание конъюнкции двух высказываний А и В является дизъюнкцией их отрицаний. Для этого надо убедится в том, что значения истинности высказываний вида
Про высказывания вида Аналогично можно доказать, что имеет место равносильность Эти равносильности носят название законов де Моргана. Из них вытекает следующее правило построения отрицания конъюнкции и дизъюнкции: чтобы построить отрицание конъюнкции (дизъюнкции), достаточно заменить отрицаниями составляющие ее высказывания, а союз «и» («или») заменить союзом «или» («и»). Задача 1. Построить отрицание высказывания «число 28 делится на 9 или на 6». Решение (два способа). 1) Поставим перед данным высказыванием слова «неверно, что». Получим высказывание «неверно, что число 28 делится на 6 или на 6», которое является отрицанием исходного. 2) Воспользуемся законом де Моргана: заменим высказывания «число 28 делится на 9» и «число 28 делится на 6» их отрицаниями, а союз «или» поменяем на союз «и». Получим высказывание «число 28 не делится на 9 и не делится на 6», которое также является отрицанием исходного. Итак, мы выяснили, как строить отрицание конъюнкции и дизъюнкции высказываний. А как быть с высказываниями, которые содержат кванторы? Достаточно ли для отрицания таких предложений поставить перед сказуемым частицу «не»? Например, будет ли отрицанием высказывания «всякий прямоугольный треугольник является равнобедренным» предложение «всякий прямоугольный треугольник не является равнобедренным»? Видим, что не будет, так как оба высказывания ложны. Таким образом, строить отрицания высказываний с квантором при помощи частицы «не» перед сказуемым нельзя. Остается другой путь – перед всем предложением, ставим слова «неверно, что». Тогда отрицанием высказывания «всякий прямоугольный треугольник является равнобедренным» будет предложение «неверно, что всякий прямоугольный треугольник является равнобедренным», но это предложение имеет тот же смысл, что и предложение «некоторые прямоугольные треугольники не являются равнобедренными». Отрицанием высказывания «некоторые прямоугольные треугольники являются равнобедренными» является высказывание «неверно, что некоторые прямоугольные треугольники являются равнобедренными». Вообще если дано предложение ("х) А(х), то его отрицанием будут предложения Получаем две равносильности:
Из них вытекает правило: для того чтобы построить отрицание высказывания, начинающегося с квантора общности (существования), достаточно заменить его квантором существования (общности) и построить отрицание предложения, стоящего после квантора. Задача 2. Построить отрицание высказывания «некоторые однозначные числа делятся на 10». Решение. Сделать это можно двумя способами. 1) Поставим перед высказыванием слова «неверно, что». Получим высказывание «неверно, что некоторые однозначные числа делятся на 10», которое является отрицанием данного. 2) Заменим квантор существования (он выражен словом «некоторые») на квантор общности «все» и построим отрицание предложения, стоящего после слова «некоторые», поставив частицу «не» перед сказуемым. Получим высказывание «все однозначные числа не делятся на 10». Последнее, о чем пойдет речь, - это отрицание высказывательных форм. Пусть на множестве Х задана высказывательная форма А(х). Ее отрицание обозначим Доказательство этого равенства мы опускаем. Пусть, например, на множестве натуральных чисел задана высказывательная форма А(х) – «число х кратно 5». Тогда ее отрицанием будет предложение «число х не кратно 5» (или «неверно, что число х кратно 5»), истинное при всех значениях х, которые не кратны 5.
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 2200; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.136.95 (0.008 с.) |

 ( читают: «не А» или «неверно, что А»).
( читают: «не А» или «неверно, что А»). , которое ложно, когда высказывание А истинно, и истинно, когда высказывание А – ложно.
, которое ложно, когда высказывание А истинно, и истинно, когда высказывание А – ложно.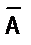
 и
и  Ú
Ú  совпадают при любых значениях истинности высказываний А и В. Сделать это можно при помощи таблицы истинности:
совпадают при любых значениях истинности высказываний А и В. Сделать это можно при помощи таблицы истинности:

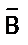
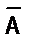 Ú
Ú 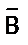
 и
и  Ú
Ú  говорят, что они равносильны, и пишут
говорят, что они равносильны, и пишут  Û
Û  Ú
Ú  .
. Û
Û  Ù
Ù  .
. и ($х)
и ($х) 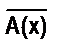 , также имеющие один и тот же смысл (и одно и то же значение истинности).
, также имеющие один и тот же смысл (и одно и то же значение истинности). Û ($х)
Û ($х)  ;
; Û ("х)
Û ("х)  .
. (читают: «не А(х)» или «неверно, что А(х)»). Предложение
(читают: «не А(х)» или «неверно, что А(х)»). Предложение  будет обращаться в истинное высказывание лишь при тех значениях х из множества Х, при которых А(х) – ложно. Таким образом,
будет обращаться в истинное высказывание лишь при тех значениях х из множества Х, при которых А(х) – ложно. Таким образом,  , где
, где  - множество истинности предложения
- множество истинности предложения  , а
, а  – дополнение множества ТА до множества Х.
– дополнение множества ТА до множества Х.


