Закон достаточного основания и аксиоматический метод в математике

В логике есть закон достаточного основания. Он утверждает, что если есть истинное суждение А, то может быть найдено такое В, из которого оно следует. При этом суждение В называется основанием для суждения А. Этот закон очень важен для математики и методики ее преподавания. Любое суждение в математике, кроме утверждений, принимаемых без доказательств и определений, не считается истинным «просто так» потому, что так кажется тому, кто его делает. Математика — это наука, логически локально упорядоченная Это значит, что любой раздел математики содержит определенные суждения, истинность которых вытекает из истинности других суждений. Эти другие суждения, в свою очередь, вытекают из других и т.д. Спрашивается, а где же исходные суждения? Ведь не может быть так, что эта цепочка следований бесконечна. Конечно, всегда есть начальные утверждения (они называются аксиомами), из которых с помощью логики и математиче­ских суждений следуют другие математические суждения. Все истинные суждения в математике, кроме аксиом и оп­ределений, оказываются, таким образом, доказываемыми. Они называются теоремами.

Приведем пример.

Почему справедлива таблица умножения? Ее правильность - это совокупность аксиом, принимаемых без доказательства, или следствие других утверждений?

Оказывается, все зависит от точки зрения. Если определить 1×2=2, 1×3=3,..., 9×9=81, 9×10=90, т.е. всю таблицу умножения в пределах 10, то получится список аксиом, который можно выучить наизусть и пользоваться им, например, при умножении столбиком и т.д.

Однако такой подход неинтересен ни с математической, ни с дидактической точки зрения. С дидактической точки зрения этот подход не объясняет, зачем вообще нужно умножение, а с математической он является неэкономным, потому что пришлось ввести слишком много аксиом. Математическая (да, пожалуй, и любая другая) теория старается обойтись минимальным количеством недоказываемых предложений (аксиом).

Поэтому вводят определенные умножения аb как а+а+.-.+а, т.е. как сумму слагаемых а, взятых b раз (b>1).

Таким образом, к моменту изучения умножения в обучении и к моменту построения теории умножения в математике сложениеуже считается изученным, и вопрос о правильности таблицы умножения получает такой ответ. Да, таблица умножения правильна, еслимы правильно складываем натуральные числа, т.е. если правильна таблица сложения.

Заметим, что проблемы обоснования очевидных и давно известных положений занимают в нашем курсе основное место. Это создает довольно большие психологические трудности в изучении материала. Итак, закон достаточного основания для математики играет огромную роль. Все утверждения математики стараются вывести из других утверждений. Те же простейшие утверждения, которые не выводятся из других утверждений, называются аксиомами, а метод построения теории на основе нескольких аксиом называется аксиоматическим методом.

 

ПРАКТИЧЕСКАЯ РАБОТА. МАТЕМАТИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО

Цель. Раскрыть особенности, структуру и способы математических доказательств. Рассмотреть правила, в соответствии с которыми стояться правильные рассуждения необходимые для обучения младших школьников обосновывать суждения в курсе начальной математики.

Теоретическая часть

Вопросы к изучению

1. Понятие умозаключения

2. Дедуктивные умозаключения

3. Индуктивные умозаключения. Полная индукция

4. Неполная индукция

5. Математическая индукция

6. Аналогия

7. Умозаключения «от противного»

8. Некоторые виды неправильных умозаключений

Основные понятия темы

Ø умозаключение,

Ø посылка и заключение,

Ø дедуктивные (правильные) умозаключения,

Ø неполная индукция,

Ø аналогия,

Ø прямое доказательство,

Ø косвенное доказательство,

Ø полная индукция.

Неполная индукция и аналогия тесно связаны с дедукцией: выводы, полученные с помощью неполной индукции и аналогии, надо либо доказывать, либо опровергать. С другой стороны, дедукция не возникает на пустом месте, а является результатом предварительного индуктивного изучения материала.

Дедуктивные умозаключения позволяют из уже имеющегося зна­ния получать новые истины, и притом с помощью рассуждения, без обращения к опыту, интуиции и т.д.

Математическое доказательство - это цепочка дедуктивных умозаключений, выполняемых по определенным правилам.

Практическая часть

1. Выскажите предположение, рассмотрев несколько частных случаев:

а) К однозначному числу приписали такую же цифру. Во сколько раз увеличилось число?

б) Имеются два числа, ни одно из них не делится на 3. Может ли (и при каком условии), сумма этих чисел разделится на 3?

в) Верно ли, что квадрат четного числа есть число, кратное 4?

2. Даны верные равенства: 74 – 47 = 27; 52 – 25 = 27; 63 – 36 = 27. Верно ли, что разность любого двузначного числа и числа, записанного теми же цифрами, но в обратном порядке, равна 27?

3. Выяснив, что (12 + 4): 2 = 12: 2 + 4: 2, ученик решил аналогично действовать при нахождении значения выражения (12 × 4): 2, и записал: (12 × 4): 2 = (12: 2) × (12: 4). Прав ли он?

4. Даны два утверждения: А (х) – «число х четное» и В (х) – «запись числа х оканчивается цифрой 4». Находятся ли они в отношении следования?

5. Почему следующее обобщение приводит к неправильному выводу: рассмотрим квадрат со стороной 1 см и измерим его углы. Все они равны 90°. Возьмем квадрат со стороной 2 см и тоже измерим все его углы. Они также получились равными 90°.Сделаем это 35 раз, предложив ученику проверить это самостоятельно. Вывод: все четырехугольники с равными сторонами имеют все углы по 90°?

6. Что играет роль отдельных подмножеств, на основании знаний о которых мы узнаем обо всем множестве в следующем умозаключении:

1 + 2 = 2 + 1; 1 + 3 = 3 + 1; 1 + 4 = 4 + 1; 1 + 5 = 5 + 1; 2 + 3 = 3 + 2;

2 + 4 = 4 + 2; 2 + 5 = 5 + 2; 3 + 4 = 4 + 3; 3 + 5 = 5 + 3; 4 + 5 = 5 + 4

Вывод. Сложение на множестве чисел {1, 2, 3, 4, 5} коммутативно.

7. Докажите, что если к произведению двух последовательных на­туральных чисел прибавить большее из них, то получится квадрат большего числа.

8. Разность двух углов равна 10°. Докажите, что эти углы не могут быть вертикальными.

9. Докажите, что если х² + 3х + 1 < 0, то х < 0.

10. Как изменится сумма двух чисел, если каждое слагаемое увели­чить в три раза?

11. Каким числом может быть сумма двух нечетных чисел? Рассмот­рите несколько частных случаев и выскажите предположение. Каким образом можно доказать его истинность?

12. Разделите каждое из чисел 3², 5² и 7² на 4. Чему в каждом из этих случаев равен остаток? Какое предположение можно высказать на основе полученных результатов? Сколько нечетных чисел нужно воз­вести в квадрат и разделить на 4, чтобы гарантировать истинность высказанного предположения?

13. Даны четыре последовательных нечетных числа. Верно ли, что произведение крайних чисел меньше произведения средних на 8?

14. Верно ли, что:

а) разность квадратов двух последовательных нечетных чисел де­лится на 8;

б) произведение двух последовательных четных чисел кратно 8;

в) разность между квадратом натурального числа, не делящегося на 3, и единицей делится на 3?

15. Покажите, что обосновывая решение следующих задач, младшие школьники могут использовать полную индукцию:

а) Дан ряд чисел: 3545, 3550, 3555, 3560, 3565. Можно ли утвер­ждать, что каждое число этого ряда делится на 5?

б) Можно ли утверждать, что значения всех нижеприведенных вы­ражений одинаковы: 326326:326; 236236:236; 626626:626.

в) Можно ли утверждать, что значения выражений в столбике одинаковы: 56:5; 7×8:(32:4); (65-9): (24:3)?

16. Закончите умозаключение так, чтобы оно было дедуктивным:

а) Если четырехугольник–прямоугольник, то в нем диагонали равны. Четырехугольник АВСD …

б) Равные треугольники имеют равные площади. Треугольники АВС и КLМ…

в) Для того чтобы ромб был квадратом, достаточно, чтобы в нем был прямой угол. Ромб АВСD…

17. Восстановите общую посылку в умозаключении:

а) Число 12 – натуральное, следовательно, оно положительное.

б) Число 15 – нечетное, следовательно, оно не делится на 2.

18. Постройте дедуктивное умозаключение, доказывающее, что 1) 130 делится на 10; 2) 137 не делится на 10; 3) Четырехугольник АВСD не является прямоугольником.

19. Докажите «от противного»:

1) что если в 10 коробках 21 елочная игрушка, то хотя бы в одной коробке лежит не менее трех елочных игрушек;

2) что множество А / (А Ç В) не пересекается с множеством В\ (А Ç В);

3) что, если а+3>10, то а ¹ 7;

4) что, если х² – четное число, то х – четно;

5) что, если отрезок, проведенный через середину одной стороны треугольника до пересечения с другой стороной, равен половине длины третьей стороны, то этот отрезок есть средняя линия треугольника.

20. Докажите, что значение выражения (х–4)(2х+1) будет целое число, если х принимает значения –1, 0, 1, 4.

21. Доказать, что каждое составное натуральное число, большее 4, но меньшее 20, представимо в виде суммы двух простых чисел.

22. Докажите, что для простого р выражение р ²+2 принимает только один раз значение простого числа.

23. Докажите методом математической индукции, что

а) 1+3+5+…+(2п–1)=п²; б) 1+3+6+…+ ;

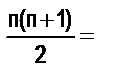
в)1²+2²+3²+…+п² = ; г) 1³+2³+3³ +…+п³ = .