
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Описанный процесс позволяет сформулировать в общем виде алгоритм вычитания чисел в десятичной системе счисления.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Записываем вычитаемое под уменьшаемым так, чтобы соответствующие разряды находились друг под другом. 2. Если цифра в разряде единиц вычитаемого не превосходит соответствующей цифры уменьшаемого, вычитаем ее из цифры уменьшаемого, записываем разность в разряд единиц искомого числа, после чего переходим к следующему разряду. 3. Если же цифра единиц вычитаемого больше единиц уменьшаемого, т.е. b0>а0, а цифра десятков уменьшаемого отлична от нуля, то уменьшаем цифру десятков уменьшаемого на 1, одновременно увеличив цифру единиц уменьшаемого на 10, после чего вычитаем из числа 10 + а0 число b0 и записываем разность в разряде единиц искомого числа, далее переходим к следующему разряду. 4. Если цифра единиц вычитаемого больше цифры единиц уменьшаемого, стоящие в разряде десятков, сотен и т.д. уменьшаемого, равны нулю, то берем первую отличную от нуля цифру в уменьшаемом (после разряда единиц), уменьшаем ее на 1, все цифры в младших разрядах до разряда десятков включительно увеличиваем на 9, а цифру в разряде единиц на 10: вычитаем b0 из 10 + а0, записываем разность в разряде единиц искомого числа и переходим к следующему разряду. 5. В следующем разряде повторяем описанный процесс. 6. Вычитание заканчивается, когда производится вычитаниеизстаршего разряда уменьшаемого. Алгоритм умножения Умножение однозначных чисел можно выполнить, основываясь на определении этого действия. Но чтобы всякий раз не обращаться к определению, все произведения однозначных чисел записывают в особую таблицу, называемую таблицей умножения однозначных чисел, и запоминают. Естественно, что смысл умножения сохраняется и для многозначных чисел, но меняется техника вычислений. Произведение многозначных чисел, как правило, находят, выполняя умножение столбиком, по определенному алгоритму. Выясним, каким образом возникает этот алгоритм, какие теоретические факты лежат в его основе. Умножим, например, столбиком 428 на 263. ´ 263 + 2568 856__ Видим, что для получения ответа нам пришлось умножить 428 на 3, 6 и 2, т.е. умножить многозначное число на однозначное; но, умножив на 6, результат записали по - особому, поместив единицы числа 2568 под десятками числа 1284, так как умножали на 60 и получили число 25680, но нуль в конце записи опустили. Слагаемое 856 - это результат умножения на 2 сотни, т.е. число 85600. Кроме того, нам пришлось найти сумму многозначных чисел. Итак, чтобы выполнять умножение многозначного числа на многозначное, необходимо уметь: - умножать многозначное число на однозначное и на степень десяти; - складывать многозначные числа. Сначала рассмотрим умножение многозначного числа на однозначное. Умножим, например, 428 на 3. Согласно правилу записи чисел в десятичной системе счисления, 428 можно представить в виде 4 × 102+2 × 10+8 и тогда 428 × 3=(4 × 102+2 × 10+8) × 3. На основании дистрибутивности умножения относительно сложения раскроем скобки: (4 × 102+(2 × 10) × 3+8 × 3. Произведения в скобках могут быть найдены по таблице умножения однозначных чисел: 12 × 102+6 × 10+24. Видим, что умножение многозначного числа на однозначное свелось к умножению однозначных чисел. Но чтобы получить окончательный результат, надо преобразовать выражение 12 × 102+6 × 10+24 - коэффициенты перед степенями 10 должны быть меньше 10. Для этого представим число 12 в виде 1·10+2, а число 24 в виде 2·10+4. Затем в выражении (1·10+2)·102+6·10+(2·10+4) раскроем скобки: 1·103+2·102+6·10+2·10+4. На основании ассоциативности сложения и дистрибутивности умножения относительно сложения сгруппируем слагаемые 6·10 и 2·10 и вынесем 10 за скобки: 1·103+2·102+(6+2)·10+4. Сумма 6+2 есть сумма однозначных чисел и может быть найдена по таблице сложения: 1· 103+2·102+8·10+4. Полученное выражение есть десятичная запись числа 1284, т. е. 428·3=1284. Таким образом, умножение многозначного числа на однозначное основывается на: - записи чисел в десятичной системе счисления; - свойствах сложения и умножения; - таблицах сложения и умножения однозначных чисел. Выведем правило умножения многозначного числа на однозначное в общем виде. Пусть требуется умножить х=аn×10n+аn–1×10n–1+…+а1×10+а0 на однозначное число у: х×у=(аn×10n+аn–1×10n–1+…+а1×10+а0)×у=(аn×у)×10n+(аn–1× у)×10n–1+…+а0×у причем преобразования выполнены на основании свойств умножения. После этого, используя таблицу умножения, заменяем все произведения аk×у, где 0£k£n, соответствующими значениями аk×у=bk×10+с и получаем: х×у=(bп×10+сп)+(bп-1×10+сп-1)×10п-1+...+(b1×10+с1)×10+(b0×10+с0)= =bп×10п+1+(сп+bп-1)×10п+...+(с1+b0)×10+с0. По таблице сложения заменяем суммы сk+bk-1, где 0£k£n и k=0,1,2,...,n, их значениями. Если, например, с0 однозначно, то последняя цифра произведения равна с0 . Если же с0=10+m0, то последняя цифра равна m0, а к скобке (с1 + b0) надо прибавить 1. Продолжая этот процесс, получим десятичную запись числа х × у. Описанный процесс позволяет сформулировать в общем видеалгоритм умножения многозначного числа 1. Записываем второе число под первым. 2. Умножаем цифры разряда единиц числа х на число у. Еслипроизведение меньше 10, его записываем в разряд единиц ответа и переходим к следующему разряду (десятков). 3. Если произведение цифр единиц числа х на число у большеили равно 10, то представляем его в виде 10q1+с0, где с0 – однозначное число; записываем с0 в разряд единиц ответа и запоминаем q1 - перенос в следующий разряд. 4. Умножаем цифры разряда десятков на число у, прибавляемк полученному произведению число q1 и повторяем процесс, описанный пп. 2 и 3. 5. Процесс умножения заканчивается, когда окажется умноженной цифра старшего разряда. Как известно, умножение числа х на число вида 10k сводится к приписыванию к десятичной записи данного числа k нулей. Покажем это. Умножим число х=аn×10n+аn–1×10n–1+…+а1×10+а0 на 10k: (аn×10n+аn–1×10n–1+…+а1×10+а0)×10k=аn×10n+k+аn–1×10n+k–1+…+а0×10k. Полученное выражение является суммой разрядных слагаемых числа an×10n+k+аn–1×10n+k–1+…+а0×10k+0×10k-1+0×10k–2+…+0×10 +0. Например, 347·103=(3·102+4·10+7)·103=3·105+4·104+7·103=3·105+4·104+7·103+0·102+ +0·10+0= =347000 Заметим еще, что умножение на число у×10k, где у – однозначное число сводится к умножению на однозначное число у и на число 10k. Например, 52×300=52×(3×102)=(52×3)×102=156×102=15600. Рассмотрим теперь алгоритм умножения многозначного числа на многозначное. Обратимся сначала к примеру, с которого начинали, т.е. к произведению 428 × 263. Представим число 263 в виде суммы 2 × 102+6 × 10+3 и запишем произведение 428 × (2 × 102 + 6 × 10 + 3). Оно, согласно дистрибутивности умножения относительно сложения, равно 428 × (2 × 102) + 428 × (6 × 10) + 428 × 3. Отсюда, применив ассоциативное свойство умножения, получим: (428 × 2) × 102+(428 × 6) × 10+428 × 3. Видим, что умножение многозначного числа 428 на многозначное число 263 свелось к умножению многозначного числа 428 на однозначные числа 2,6 и 3, а также на степени 10. Рассмотрим умножение многозначного числа на многозначное в общем виде. Пусть х и у - многозначные числа, причем у=bm×10m+bm–1×10m–1+…+b0. В силу дистрибутивности умножения относительно сложения, а также ассоциативности умножения можно записать: х×у=х×(bm×10m+bm–1×10m–1+…+b0)=(х×bm)×10m+(х×bm–1)×10m–1+…+b0×х. Последовательно умножая число х на однозначные числа bm, bm–1, …, b0, а затем на 10m, 10m–1, …, 1, получаем слагаемые, сумма которых равна х× у. Сформулирует в общем виде алгоритм умножения числа х= 1. Записываем множитель х под ним второй множитель у. 2. Умножаем число х на младший разряд b0 числа у и записываем произведение х × b0 под числом у. 3. Умножаем число х на следующий разряд b1 числа у и записываем произведение х×b1, но со сдвигом на один разряд влево, что соответствует умножению х × b1 на 10. 4. Продолжаем вычисление произведений до вычисления х×bk. 5. Полученные k+1 произведения складываем. Изучение алгоритма умножения многозначных чисел в начальном курсе математики, как правило, проходит в соответствии с выделенными этапами. Различия имеются только в записи. Например, при обосновании случая умножения многозначного числа на однозначное пишут: 428 × 3 = (400 + 20 + 8) × 3 = 400× 3 + 20× 3 + 8× 3 = 1200 + 60 + 24 = 1284. Основой выполненных преобразований являются: - представление первого множителя в виде суммы разрядных слагаемых (т.е. запись числа в десятичной системе счисления); - правило умножения суммы на число (или дистрибутивность умножения относительно сложения); - умножение «круглых» (т.е. оканчивающихся нулями) чиселна однозначное число, что сводится к умножению однозначных чисел. Алгоритм деления Когда речь идет о технике деления чисел, то этот процесс рассматривают как действие деления с остатком: разделить целое неотрицательное число а на натуральное число b - это значит найти такие целые неотрицательные числа q r, что а = bq + r, причем 0 £ r < b. Выясним сначала, как осуществляется деление на однозначное число. Если на однозначное число делят однозначное или двузначное (не превышающее 89), то используется таблица умножения однозначных чисел. Например, частным чисел 54 и 9 будет число 6, так как 9 × 6 = 54. Если же надо разделить 51 на 9, то находят ближайшее к нему меньшее число, которое делится на 9 - это число 45, и, следовательно, неполным частным при делении 51 на 9 будет число 5. Чтобы найти остаток, надо из 51 вычесть 45: 51 - 45 = 6. Таким образом, 51 = 9×5 + 6, т.е. при делении 51 на 9 получается неполное частное 5 и остаток, равный 6. Записать это можно иначе, при помощи деления уголком: 51 9 - 45 5 Будем теперь делить трехзначное число на однозначное, например, 378 на 4. Разделить 378 на 4 - это значит найти такое неполное частное q и остаток r, что 378=4q+r, причем остаток r должен удовлетвори условию 0£r<b, а неполное частное q - условию 4q£ 378<4(q+1). Определим, сколько цифр будет содержаться в записи числа q. Однозначным число q быть не может, так как тогда произведение 4q может быть максимально равно 36 и, значит, не будут выполняться условий сформулированные выше для r и q. Если число q двузначное, т.е. есть 10<q<100, то тогда 40<4q<400 и, следовательно, 40<378<400, что верно. Значит, частное чисел 378 и 4 - число двузначное. Чтобы найти цифру десятков частного, умножим последовательно делитель 4 на 20, 30, 40 и т.д. Поскольку 4×90=360, а 4×100=400, и 360<378<400, то неполное частное заключено между числами90 и100, т.е. q=90+q0. Но тогда должны выполняться неравенства: 4×(90+q0)£ 378<4×(90q+q0+1), откуда 360+4q0£78<360+4(q0+1) и 4q0£18<4(q0+1). Число q0 (цифра единиц частного), удовлетворяющее последнему неравенству, можно найти подбором, воспользовавшись таблицей умножения. Получаем, что q0=4 и, следовательно, неполное частное q=90+4=94. Остаток находится вычитание: 378–4×94=2. Итак, при делении числа 378 на 4 получается неполное частное 94 и остаток 2: 378–4×94+2. Описанный процесс является основой деления уголком: 378 4 - 36 94 - 16 Аналогично выполняется деление многозначного числа на многозначное. Разделим, например, 4316 на 52. Выполнить это деление - значит найти такие целые неотрицательные числа q и r, что 4316=52q+r, 0£r < 52, а неполное частное должно удовлетворять неравенству 52q£ 4316<52(q+1). Определим число цифр в частном q. Очевидно, частное заключено между числами 10 и 100 (т.е. q - двузначное число), так как 520<4316<5200. Чтобы найти цифру десятков частного, умножим последовательно делитель 52 на 20, 30, 40, 50 и т.д. Поскольку 52 × 80=4160, а 52 × 90=4680 и 4160<4316<4680, то неполное частное заключено между числами 80 и 90, т.е. q=80+q0. Но тогда должны выполняться неравенства: 52 × (80+q0)£ 4316< 52 × (80+q0 +1), 4160+52q0 £ 4316<4160+52 × (q0+1), 52q0 £156<52 × (q0+1). Число q0 (цифру единиц частного), удовлетворяющее последнему неравенству, можно найти подбором: 156=52 × 3, т.е. имеем случай, когда остаток равен 0. Следовательно, при делении 4316 на 52 получается частное 83.
Приведенные рассуждения лежат в основе деления уголком: 4316 52 - 416 83 - 156
|
||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 857; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.011 с.) |

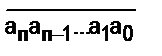 на однозначное число у.
на однозначное число у. , так как равно
, так как равно на число у =
на число у =  .
.


