Понятие алгоритма и его свойства

Понятие алгоритма и его свойства

Каждый из нас постоянно решает множество задач: как быстрее добраться на работу, как лучше спланировать дела текущего дня и многие другие. Некоторые задачи мы решаем автоматически, так как на протяжении многих лет привыкли к их выполнению, другие требуют длительного размышления над решением, но в любом случае, решение каждой задачи всегда делится на простые действия.

Алгоритм – описанная на некотором языке точная конечная система правил, определяющая содержание и порядок действий над некоторыми объектами, строгое выполнение которых дает решение поставленной задачи. Понятие алгоритма, являющееся фундамен­тальным в математике и информатике, возникло задолго до появле­ния средств вычислительной техники. Слово «алгоритм» появилось в средние века, когда европейцы познакомились со способами вы­полнения арифметических действий в десятичной системе счисления, описанными узбекским математиком Муххамедом бен Аль-Хорезми («аль-Хорезми» – человек из города Хорезми; в настоящее время город Хива в Хорезмской области Узбекистана). Слово алгоритм – есть результат европейского произношения слов аль-Хорезми. Первоначально под алгоритмом понимали способ выполнения арифметических действий над десятичными числами. В дальнейшем это понятие стали использовать для обозначения любой последовательности действий, приводящей к решению поставленной задачи.

Любой алгоритм существует не сам по себе, а предназначен для определенного исполнителя (человека, робота, компьютера, языка программирования и т.д.). Свойством, характеризующим любого исполнителя, является то, что он умеет выполнять некоторые команды. Совокупность команд, которые данный исполнитель умеет выполнять, называется системой команд исполнителя. Алгоритм описывается в командах исполнителя, который будет его реализовывать. Объекты, над которыми исполнитель может совершать действия, образуют так называемую среду исполнителя. Исходные данные и результаты любого алгоритма всегда принадлежат среде того исполнителя, для которого предназначен алгоритм.

Значение слова «алгоритм» очень схоже со значениями слов «рецепт», «метод», «процесс». Однако, в отличие от рецепта или процесса, алгоритм характеризуется следующими свойствами:

­ дискретность (разрывность - противоположно непрерывности) – это свойство алгоритма, характеризующее его структуру: каждый алгоритм состоит из отдельных законченных действий, говорят: «Делится на шаги»;

­ массовость – применимость алгоритма ко всем задачам рассматриваемого типа, при любых исходных данных. Например, алгоритм решения квадратного уравнения в области действительных чисел должен содержать все возможные исходы решения, т.е., рассмотрев значения дискриминанта, алгоритм находит либо два различных корня уравнения, либо два равных, либо делает вывод о том, что действительных корней нет;

­ определенность (детерминированность, точность) – свойство алгоритма, указывающее на то, что каждый шаг алгоритма должен быть строго определен и не допускать различных толкований; также строго должен быть определен порядок выполнения отдельных шагов. Помните сказку про Ивана-царевича? «Шел Иван-царевич по дороге, дошел до развилки. Видит большой камень, на нем надпись: «Прямо пойдешь – голову потеряешь, направо пойдешь – жену найдешь, налево пойдешь – разбогатеешь». Стоит Иван и думает, что дальше делать». Таких инструкций алгоритм содержать не может;

­ результативность – свойство, состоящее в том, что любой алгоритм должен завершаться за конечное (может быть очень большое) число шагов. Вопрос о рассмотрении бесконечных алгоритмов остается за рамками теории алгоритмов;

­ формальность – это свойство указывает на то, что любой исполнитель, способный воспринимать и выполнять инструкции алгоритма, действует формально, т.е. отвлекается от содержания поставленной задачи и лишь строго выполняет инструкции. Рассуждать «что, как и почему?» должен разработчик алгоритма, а исполнитель формально (не думая) поочередно исполняет предложенные команды и получает необходимый результат.

Способы описания алгоритмов

Рассмотрим следующие способы описания алгоритма: словесное описание, псевдокод, блок-схема, программа.

Словесное описание представляет структуру алгоритма на естественном языке. Например, любой прибор бытовой техники (утюг, электропила, дрель и т.п.) имеет инструкцию по эксплуатации, т.е. словесное описания алгоритма, в соответствии которому данный прибор должен использоваться.

Никаких правил составления словесного описания не существует. Запись алгоритма осуществляется в произвольной форме на естественном, например, русском языке. Этот способ описания не имеет широкого распространения, так как строго не формализуем (под «формальным» понимается то, что описание абсолютно полное и учитывает все возможные ситуации, которые могут возникнуть в ходе решения); допускает неоднозначность толкования при описании некоторых действий; страдает многословностью.

Псевдокод – описание структуры алгоритма на естественном, частично формализованном языке, позволяющее выявить основные этапы решения задачи, перед точной его записью на языке программирования. В псевдокоде используются некоторые формальные конструкции и общепринятая математическая символика.

Строгих синтаксических правил для записи псевдокода не существует. Это облегчает запись алгоритма при проектировании и позволяет описать алгоритм, используя любой набор команд. Однако в псевдокоде обычно используются некоторые конструкции, присущие формальным языкам, что облегчает переход от псевдокода к записи алгоритма на языке программирования. Единого или формального определения псевдокода не существует, поэтому возможны различ­ные псевдокоды, отличающиеся набором используемых слов и конструкций.

Блок-схема – описание структуры алгоритма с помощью геометрических фигур с линиями-связями, показывающими порядок выполнения отдельных инструкций. Этот способ имеет ряд преимуществ. Благодаря наглядности, он обеспечивает «читаемость» алгоритма и явно отображает порядок выполнения отдельных команд. В блок-схеме каждой формальной конструкции соответствует определенная геометрическая фигура или связанная линиями совокупность фигур.

Рассмотрим некоторые основные конструкции, использующиеся для построения блок-схем.

Блок, характеризующий начало/конец алгоритма (для подпрограмм – вызов/возврат):

Блок – процесс, предназначен­ный для описания отдельных действий:

Блок – предопределенный про­цесс, предназначенный для обращения к вспомогательным алгоритмам (подпрограммам):

Блок – ввода/вывода с неопределенного носителя:

Блок – ввод с клавиатуры:

Блок – вывод на монитор:

Блок – вывод на печатающее устройство:

С Начало j ( Конец J

<Действие>

Г/

Блок – решение (проверка усло­вия или условный блок):

Блок, описывающий цикл с па­раметром:

Нет

Да

<тело цикла>

Блок — границы цикла, описыва­ющий циклические процессы типа: «цикл с предусловием», «цикл с постусловием»:

<тело цикла>

Соединительные блоки

Описания алгоритма в словесной форме, на псевдокоде или в виде блок-схемы допускают некоторый произвол при изображении команд. Вместе с тем она настолько достаточна, что позволяет человеку понять суть дела и исполнить алгоритм. На практике исполнителями алгоритмов выступают компьютеры. Поэтому алгоритм, предназначенный для исполнения на компьютере, должен быть записан на «понятном» ему языке, такой формализованный язык называют языком программирования.

Программа – описание структуры алгоритма на языке алгорит­мического программирования. С другой стороны, понятие «програм­ма» нельзя трактовать только таким образом, как уже говорилось в главе 5 (п. 5.5.2), программа на языке декларативного программиро­вания представляет собой совокупность описанных знаний и не со­держит явного алгоритма исполнения.

Пример 6.2.

Вывести значение наибольшего из двух чисел. Псевдокод:

1. Ввод двух чисел а, Ь.

2. ЕСЛИ а > Ъ, ТО «выводим а»,

ИНАЧЕ «выводим Ь».

3. Конец.

297

Ложь (Нет)

Рис. 6.3. Неполное ветвление

( Начало J

I

/Ввод /

/ «■* /

Нет

Да

Рис. 6.4. Блок-схема к примеру 6.2

В данном примере реализовано полное ветвление. ЕСЛИ значе­ния входных данных таковы, что а > Ь, ТО выполняется линейный алгоритм:

1. Ввод двух чисел а, Ь.

2. Вывод а.

ИНАЧЕ, когда а <Ь, выполняется линейный алгоритм:

1. Ввод двух чисел а, Ь.

2. Вывод Ь.

Вывод: алгоритм является разветвляющимся и состоит из двух ветвей.

Рассмотрим стандартный алгоритм поиска наибольшего (наименьшего) значения среди не­скольких заданных. Основная идея алгоритма сводится к следу­ющему: за наибольшее (наимень­шее) принимаем значение лю­бого из данных. Поочередно сравниваем оставшиеся данные с наибольшим (наименьшим). Если окажется, что очередное значение входного данного боль­ше (меньше) наибольшего (наи­меньшего), то наибольшему (наименьшему) присваиваем это значение. Таким образом, срав­нив все входные данные, найдем наибольшее (наименьшее) среди них. Алгоритм использует непол­ное ветвление.

Пример 6.3.

Заданы три числа. Найти значение наименьшего из них.

Заданные числа обозначим: а, Ь, с; результирующее наимень­шее — тт. На рис. 6.5 представ­лена блок-схема алгоритма реше- р_Ис. 6.5. Алгоритм поиска ния данной задачи. наименьшего значения

среди трех заданных

КолланЭа «Выбор»

Часто при выборе одного из возможных вариантов действий при­ходится проверять значение выражения на принадлежность заданно­му набору данных. Для этого существует команда «Выбор». При ее исполнении сначала вычисляется значение некоторого выражения Z. Затем последовательно проверяются условия VI, V2,..., V«относи­тельно Z, начиная с первого, до тех пор, пока не встретится усло­вие, принимающее значение ИСТИНА. Далее выполняется соответ­ствующее этому условию действие (или серия действий), после чего команда выбора завершается. Если ни одно из условий не является истинным, то выполняется действие (или набор действий), идущее по ветви ЛОЖЬ для каждого из условий. На рис. 6.6 представлена блок-схема команды «Выбор» для п = 3.

Правило изменения параметра и i = TV, К, h означает
1-й шаг цикла	/ = N
2-й шаг цикла	/ = N + h
3-й шаг цикла и т.д.	/ = N + 2h
последний шаг	г = К

Рис. 6.6. Команда «выбор»

Арифметический цикл

В арифметическом цикле число его шагов (повторений) однозначно определяется правилом изменения параметра, которое задается с помощью начального (N) и конечного (К) значений параметра и шагом (h) его изменения. Т.е., на первом шаге цикла значение па­раметра равно N, на втором - N + h, на третьем - N + 2h и т.д. На последнем шаге цикла значение параметра не больше К, но та­кое, что дальнейшее его изменение приведет к значению, большему, чем К.

Пример 6.4.

Вывести 10 раз слово «Привет!».

Параметр цикла обозначим /, он будет отвечать за количество выведенных слов. При / = 1 будет выведено первое слово, при / = 2 будет выведено второе слова и т.д. Так как требуется вывести 10 слов, то последнее значение параметра / = 10. В заданном примере требу­ется 10 раз повторить одно и то же действие: вывести слово «При-

301вет!». Составим алгоритм, ис­пользуя арифметический цикл, в котором правило изменения параметра / = 1,10,1. Т.е. на­чальное значение параметра /= 1; конечное значение/= 10; шаг изменения И = 1. На рис. 6.7 представлена блок-схема алгоритма решения данной за­дачи.

Привет! J ( Конец J

Рис. 6.7. Блок-схема к примеру 6.4

Цикл с предусловием

Количество шагов цикла заранее не определено и зависит от входных данных задачи. В данной циклической структуре сначала проверяется значение условного выражения (условие) перед выпол­нением очередного шага цикла. Если значение условного выражения истинно, исполняется тело цикла. После чего управление вновь пе­редается проверке условия и т.д. Эти действия повторяются до тех пор, пока условное выражение не примет значение ЛОЖЬ. При пер­вом же несоблюдении условия цикл завершается.

 

 

 

 

 

 

	^^ Условие ^^>	Условие |
	+ |
Да		Тело цикла
	Тело цикла
	а			б

Рис. 6.8. Блок-схема цикла с предусловием

Блок-схема данной конструкции представлена на рис. 6.8'двумя способами: с помощью условного блока а и с помощью блока гра­ницы цикла б.

Особенностью цикла с предусловием является то, что если из­начально условное выражение ложно, то тело цикла не выполнится ни разу.

Пример 6.5.

Одним из наиболее распространенных алгоритмов, встречаю­щихся в литературе по информатике, является алгоритм Евклида -алгоритм нахождения наибольшего общего делителя двух натураль­ных чисел тип (рис.6.9).

Рис. 6.9. Блок-схема алгоритма Евклида

303Опишем его на псевдокоде:

1. Ввод натуральных чисел тип.

2. Пока т t- n делать.

2.1. Если т>п, то т=т — п, иначе п— п — т.

2.2. Переход к шагу 2.

3. Вывод т (найденный наибольший общий делитель).

4. Конец.

Цикл с постусловием

Как и в цикле с предусловием, в циклической конструкции с постусловием заранее не определено число повторений тела цикла, оно зависит от входных данных задачи. В отличие от цикла с пред­условием, тело цикла с постусловием всегда будет выполнено хотя бы один раз, после чего проверяется условие. В этой конструкции тело цикла будет выполняться до тех пор, пока значение условного выражения ложно. Как только оно становится истинным, выполне­ние команды прекращается. Блок-схема данной конструкции пред­ставлена на рис. 6.10 двумя способами: с помощью условного блока а и с помощью блока управления б.

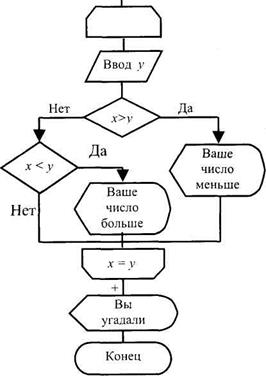
Тело цикла

I

Условие

а

Рис. 6.10. Блок-схема цикла с постусловием

Пример 6.6.

Составим алгоритм игры «Угадай число». Первый игрок вводит задуманное число от 1 до 50. Второй (угадывающий) вводит другое число и получает один из ответов: «Ваше число меньше», «Ваше чис­ло больше» или «Вы угадали». Игра продолжается до тех пор, пока второй игрок не угадает задуманное число.

Составляя алгоритм игры, обозначим х - число, задуманное пер­вым игроком, у — число, вводимое на очередном шаге вторым игро­ком. Блок-схема алгоритма приведена на рис. 6.11.

С Начало J

I / Ввод х /

Рис. 6.11. Блок-схема игры «Угадай число» (пример 6.6)

305Рассмотрим стандартные циклические алгоритмы, такие как вы­числение суммы и подсчет количества элементов, удовлетворяющих некоторому признаку.

Суммирование.

Пример 6.7.

Для заданного натурального числа N вычислить сумму

2 3 N

Подсчет суммы осуществляется следующим образом. Сначала счи- ' таем, что сумма S есть первое слагаемое (S = 1). Далее к первому сла-

1 гаемому прибавляем второе, получаем новую сумму 5 = 1 + —. Но

на предыдущем шаге S = 1, поэтому можно записать S = S + —. к сум­ме двух первых слагаемых прибавляем третье 5 = 1 + — + -. Но на

1 1 предыдущем шагу 5 = 1 + —, поэтому можно записать S = S + - и т.д.

2 3

Получили следующую последовательность шагов: 1) S = 1.

2)

3)

2" 3'

Запишем /-и шаг, опираясь на два предыдущих:

i

Выясним правило изменения номера шага /. В описанной по­следовательности / = 1, 2, 3 и т.д. В сумме N слагаемых, поэтому по­следним значением / будет N. Отсюда нашли правило изменения / = 1, N, 1.

Сверяя инструкции каждого шага, находим, что выражение на первом шаге отличается от других (однотипных). Чтобы оно стало таким как все, в сумму надо добавить S, т.е. записать: S = S + 1 (учи-

1 тываем, что 1 ⁼ 7)- Отсюда для S возникает необходимость задания

начального значения, но такого, чтобы S + 1 = 1 (таким должно быть выражение для / = 1), этим числом является нуль, при сложении с нулем сумма не меняется.

Так как известно число шагов цикла, то для построения алго­ритма используем цикл с параметром /.

Алгоритм на псевдокоде:

1. Ввод N..

2. S = 0. "

3. Для / = 1, N, 1 повторить:

3.1. S =

4. Вывод S.

5. Конец.

Блок-схема алгоритма приведена на рис. 6.12.

Сформулируем правило суммирования:

• начальное значение суммы S = 0;

• в теле некоторой циклической конструкции выполнить команду:

S = S + <слагаемое>.

Упражнения для самостоятельной работы:

Для заданного натурального числа N вычислите суммы N-сла-гаемых:

12 3

1. - + - + - +...; 2 3 4

12 3

2. - + - + - +...; 2 4 6

3073.

sin 1

sin 2

sin3

+ 1 + 2 1+2+3

+...

( Начало J

S = 0

 

s = s + -

( Конец j

Рис. 6.12. Алгоритм вычисления суммы

Подсчет количества элементов. Произведем счет: 1, 2, 3, 4, 5 и т.д., этот процесс является циклическим, так как каждый раз мы со­вершаем одно и то же действие: предыдущее натуральное число уве­личиваем на единицу. Обозначив через К - счетчик искомых эле­ментов, легко получить правило счетчика: К = К + 1 (на очередном шаге цикла). Но при первом подсчете должны получить значение К, равное единице, а до начала счета счетчик должен быть пуст, следо­вательно, начальное значение счетчика равно нулю.

Правило счетчика:

• начальное значение счетчика К = 0;

• в теле некоторой циклической конструкции выполнить команду:

К = К + 1.

Пример 6.8

Задано 20 чисел. Сколько среди них чисел, больших 10? Псевдокод:

1. К = 0 {Счетчик чисел, больших 10}.

2. Повторить 20 раз (для / = 1, 20, 1).

2.1. Ввод числа х.

2.2. Если х > 10, то К = К+ 1.

3. Вывод К.

4. Конец.

Блок-схема алгоритма приведена на рис. 6.13. Замечание: в фигурных скобках {....} принято помещать ком­ментарии к алгоритму.

Рис. 6.13. Алгоритм примера 6.8

309В каждом из рассмотренных выше примеров использовалась одна циклическая конструкция. В реальных задачах может встретиться любое число циклов. Обозначив цикл квадратной скобкой, схематич­но представим варианты взаимного расположения циклов (рис. 6.14).

а - последовательные б — вложенные в - запрещенные

Рис. 6.14. Расположение циклов

Алгоритм любой задачи может быть представлен как комбина­ция представленных выше элементарных алгоритмических структур, поэтому данные конструкции: линейную, ветвящуюся и цикличес­кую, называют базовыми.

Рекурсивный алгоритм

Рекурсивным называется алгоритм, организованный таким образом, что в процессе выполнения команд на каком-либо шаге он прямо или косвенно обращается сам к себе.

Блок-схема

Рис. 6.15. Ввод элементов одномерного массива А(10)

Пример 6.9. -»

Рассмотрим алгоритм вычисления среднего арифметического по­ложительных элементов числового массива А(10).

Среднее арифметическое есть отношение суммы к числу ее сла­гаемых, т.е.

среднее арифметическое —

Алгоритм решения задачи (рис. 6.16) будет содержать подсчет суммы (обозначим ее S), включающей положительные элементы мас­сива (а. > 0), и количества (обозначим N) ее слагаемых.

Псевдокод:

1. Повторить 10 раз (для i = 1, 10, 1). 1.1. Ввод а.

2. Начальное значение суммы: S = 0.

3. Начальное значение счетчика: N = 0.

4. Повторить 10 раз (для /= 1, 10, 1):

4.1. ЕСЛИ а. > 0, ТО S = S + а.; N = N + 1.

5. ЕСЛИ N > 0, ТО вычисление среднего арифметического SA = S/N; вывод SA.

ИНАЧЕ: вывод «Положительных элементов в массиве нет».

6. Конец.

313 С Начало 1

" '■'»■■

>-;

S = 0

N = 0

 

	10, 1
ч"^1.	У
		^> | Да
Нет		S = S +я,
		i
		N = N+1

Нет

Да

Положительных элементов нет

Рис. 6.16. Блок-схема задачи «подсчета среднего арифметического положительных элементов массива» (пример 6.9)

( Начало J

щ

т= 1

X^i = 2,10,

Пример 6.10.

В заданном числовом массиве А(10) найти наиболь­ший элемент и его индекс, при условии, что такой эле­мент в массиве существует, и единственный.

Обозначим индекс наи­большего элемента т. Будем считать, что первый элемент массива является наиболь­шим (т = 1). Сравним пооче­редно наибольший с осталь­ными элементами массива. Если оказывается, что теку­щий элемент массива о. (тот, с которым идет сравнение) больше выбранного нами наибольшего а, то считаем его наибольшим (т = i) (рис. 6.17).

Рассмотрим двумерный массив (шкаф с множеством ящиков, положение которых определяется двумя коорди­натами — по горизонтали и по вертикали). В математике двумерный массив (таблица чисел) называется матрицей. Каждый ее элемент имеет два

индекса а.., первый индекс / определяет номер строки, в которой на­ходится элемент (координата по горизонтали), а второй j — номер столбца (координата по вертикали). Двумерный массив характеризу­ется двумя размерностями N и М, определяющими число строк и столбцов соответственно (рис. 6.18).

Ввод элементов двумерного массива осуществляется построчно, в свою очередь, ввод каждой строки производится поэлементно, тем

а_т,т

(

-Г

Конец

Рис 6.17. Алгоритм поиска

наибольшего элемента массива

и его индекса (пример 6.10)

Языки программирования

Как мы уже знаем, компьютерная программа представляет собой логически упорядоченную последовательность команд, предназначенных для управления компьютером. Процессор компьютера - это большая интегральная схема. Все данные и команды он получает в виде электрических сигналов. В двоичном коде наличие сигнала описывается понятием «1», а его отсутствие - понятием «0». Команды, обрабатываемые процессором, можно интерпретировать как ряд чередующихся определенным образом единиц и нулей. То есть любая команда преобразуется в двоичное число. Таким образом, процессор исполняет программы, представляющие собой последовательность чисел и называемые машинным кодом.

Писать программы в машинных кодах очень сложно, причем с ростом размера программы эта задача усложняется. В компьютерах первого поколения использовались программы, написанные в машинных кодах, причем для каждого компьютера существовал свой собственный машинный код. Числовая кодировка команд, адресов ячеек и обрабатываемых данных, зависимость вида программы от ее места в памяти не давали возможность следить за смыслом программы. Это во многом ограничивало область применения компьютеров первого поколения. В тот период (начало 50-х гг.) средства программирования и программное обеспечение только зарождались и были еще не развиты. Для того чтобы сделать программу читабельной и иметь возможность следить за ее смысловой структурой, придумали символический язык ассемблер, близкий к машинному (конец 50-х -начало 60-х гг.), в котором появилось понятие переменной. Ассемблер стал первым полноценным языком программирования. Благодаря этому заметно уменьшилось время разработки и возросла надежность программ. Для записи кодов операций и обрабатываемой информации в ассемблере используются стандартные обозначения, позволяющие записывать числа и текст в общепринятом виде, для кодов команд приняты мнемонические обозначения. Для обозначения величин, размещаемых в памяти, можно применять имена. После ввода программы ассемблер сам заменяет символические имена на адреса памяти, а символические коды команд на числовые. Использование ассемблера сделало процесс программирование более наглядным. Дальнейшее развитие этой идеи привело к созданию языков программирования высокого уровня, в которых длинные и сложные последовательности машинных кодов были заменены одним единственным обозначающим их словом – операторы.

Системы программирования

Процесс создания программы включает:

• Составление исходного кода программы (рис. 6.21) на языке про­граммирования.

• Этап трансляции, необходимый для создания объектного кода

программы.

• Построение загрузочного модуля, готового к исполнению.

Все перечисленные выше действия требуют наличия специаль­ных программных средств.

Исходны!П| Трансляция Ц рбГектный Ц Редактор II Загрузочный

^' """ Ч ~ II МОДУЛЬ

Код

Код

связей

модуль

Рис. 6.21. Процесс создания программы, готовой к исполнению Совокупность этих программных средств входит в состав систе­мы программирования:

• Текстовый редактор (необходимый для создания и редактирова­ния исходного кода программы на языке программирования).

• Компилятор.

• Редактор связей.

• Отладчик.

• Библиотеки функций.

• Справочная система.

Языки моделирования

При моделировании систем применяются формальные способы их описания - формальные нотации, с помощью которых можно представить объекты и взаимосвязи между ними в системе. Такие системы называют CASE-системами.

4.6. Этапы подготовки и решений на компьютере

Компьютер предназначен для решения разнообразных задач: научно-технических, инженерных, разработки системного программ­ного обеспечения, обучения, управления производственными процес­сами и т.д. В процессе подготовки и решения на компьютере науч­но-технических задач можно выделить следующие этапы:

1. Постановка задачи – формулируется цель решения задачи, под­робно описывается ее содержание; проводится анализ условий, при которых решается поставленная задача, выявляется область определения входных параметров задачи.

2. Формальное построение модели задачи – предполагает построение модели с характеристиками, адекватными оригиналу, на основе какого-либо его физического или информационного принципа; анализируется характер и сущность величин, используемых в задаче.

3. Построение математической модели задачи – характеризуется математической формализацией задачи, при которой существу­ющие взаимосвязи между величинами выражаются с помощью математических соотношений. Как правило, математическая мо­дель строится с определенной точностью, допущениями и огра­ничениями.

4. Выбор и обоснование метода решения - модель решения задачи реализуется на основе конкретных приемов и методов решения. В большинстве случаев математическое описание задачи трудно перевести на машинный язык. Выбор и использование метода решения позволяет свести решение задачи к конкретному набо­ру машинных команд. При обосновании метода решения рас­сматриваются вопросы влияния различных факторов и условий на конечный результат, в том числе на точность вычислений, время решения задачи на компьютере, требуемый объем памяти и др.

5. Построение алгоритма — на данном этапе составляется алгоритм решения задачи, в соответствии с выбранным методом решения. Процесс обработки данных разбивается на отдельные относи­тельно самостоятельные блоки, определяется последовательность выполнения этих блоков.

6. Составление программы — алгоритм решения переводится на кон­кретный язык программирования.

7. Отладка программы — процесс устранения синтаксических и ло­гических ошибок в программе. В процессе трансляции програм­мы с помощью синтаксического и семантического контроля вы­являются недопустимые конструкции и символы (или сочетания символов) для данного языка программирования. Компьютер выдает сообщение об ошибках в форме, соответствующей этому языку. Затем проверяется логика работы программы в процессе ее выполнения с конкретными исходными данными. Для этого используются специальные методы. Например, в программе вы­бираются контрольные точки, для них подбираются тестирую­щие примеры и вручную находятся значения в этих точках, ко­торые затем и сверяются со значениями, получаемыми компьютером на этапе отладки. Кроме того, используются отлад­чики, выполняющие специальные действия на этапе отладки, такие как удаление, замена или вставка отдельных операторов

• или целых фрагментов программы, вывод промежуточных ре­зультатов, изменение значений заданных переменных и др.

8. Решение задачи на компьютере и анализ результатов. Теперь про­грамму можно использовать для решения поставленной задачи. Первоначально выполняется многократное решение задачи на компьютере для различных наборов исходных данных. Получае­мые результаты анализируются специалистом, поставившим за­дачу. Разработанная программа поставляется заказчику в виде готовой к исполнению машинной программы. К ней прилагает­ся документация, включающая инструкцию по эксплуатации.

В задачах другого типа некоторые этапы могут отсутствовать. Например, проектирование программного обеспечения не требует построения математической модели.

Все приведенные этапы тесно связаны между собой. Например, анализ результатов может привести к необходимости внесения изме­нений в программу, алгоритм, метод решения или даже в постанов­ку задачи.

 

Понятие алгоритма и его свойства

Каждый из нас постоянно решает множество задач: как быстрее добраться на работу, как лучше спланировать дела текущего дня и многие другие. Некоторые задачи мы решаем автоматически, так как на протяжении многих лет привыкли к их выполнению, другие требуют длительного размышления над решением, но в любом случае, решение каждой задачи всегда делится на простые действия.

Алгоритм – описанная на некотором языке точная конечная система правил, определяющая содержание и порядок действий над некоторыми объектами, строгое выполнение которых дает решение поставленной задачи. Понятие алгоритма, являющееся фундамен­тальным в математике и информатике, возникло задолго до появле­ния средств вычислительной техники. Слово «алгоритм» появилось в средние века, когда европейцы познакомились со способами вы­полнения арифметических действий в десятичной системе счисления, описанными узбекским математиком Муххамедом бен Аль-Хорезми («аль-Хорезми» – человек из города Хорезми; в настоящее время город Хива в Хорезмской области Узбекистана). Слово алгоритм – есть результат европейского произношения слов аль-Хорезми. Первоначально под алгоритмом понимали способ выполнения арифметических действий над десятичными числами. В дальнейшем это понятие стали использовать для обозначения любой последовательности действий, приводящей к решению поставленной задачи.

Любой алгоритм существует не сам по себе, а предназначен для определенного исполнителя (человека, робота, компьютера, языка программирования и т.д.). Свойством, характеризующим любого исполнителя, является то, что он умеет выполнять некоторые команды. Совокупность команд, которые данный исполнитель умеет выполнять, называется системой команд исполнителя. Алгоритм описывается в командах исполнителя, который будет его реализовывать. Объекты, над которыми исполнитель может совершать действия, образуют так называемую среду исполнителя. Исходные данные и результаты любого алгоритма всегда принадлежат среде того исполнителя, для которого предназначен алгоритм.

Значение слова «алгоритм» очень схоже со значениями слов «рецепт», «метод», «процесс». Однако, в отличие от рецепта или процесса, алгоритм характеризуется следующими свойствами:

­ дискретность (разрывность - противоположно непрерывности) – это свойство алгоритма, характеризующее его структуру: каждый алгоритм состоит из отдельных законченных действий, говорят: «Делится на шаги»;

­ массовость – применимость алгоритма ко всем задачам рассматриваемого типа, при любых исходных данных. Например, алгоритм решения квадратного уравнения в области действительных чисел должен содержать все возможные исходы решения, т.е., рассмотрев значения дискриминанта, алгоритм находит либо два различных корня уравнения, либо два равных, либо делает вывод о том, что действительных корней нет;

­ определенность (детерминированность, точность) – свойство алгоритма, указывающее на то, что каждый шаг алгоритма должен быть строго определен и не допускать различных толкований; также строго должен быть определен порядок выполнения отдельных шагов. Помните сказку про Ивана-царевича? «Шел Иван-царевич по дороге, дошел до развилки. Видит большой камень, на нем надпись: «Прямо пойдешь – голову потеряешь, направо пойдешь – жену найдешь, налево пойдешь – разбогатеешь». Стоит Иван и думает, что дальше делать». Таких инструкций алгоритм содержать не может;

­ результативность – свойство, состоящее в том, что любой алгоритм должен завершаться за конечное (может быть очень большое) число шагов. Вопрос о рассмотрении бесконечных алгоритмов остается за рамками теории алгоритмов;

­ формальность – это свойство указывает на то, что любой исполнитель, способный воспринимать и выполнять инструкции алгоритма, действует формально, т.е. отвлекается от содержания поставленной задачи и лишь строго выполняет инструкции. Рассуждать «что, как и почему?» должен разработчик алгоритма, а исполнитель формально (не думая) поочередно исполняет предложенные команды и получает необходимый результат.

Способы описания алгоритмов

Рассмотрим следующие способы описания алгоритма: словесное описание, псевдокод, блок-схема, программа.

Словесное описание представляет структуру алгоритма на естественном языке. Например, любой прибор бытовой техники (утюг, электропила, дрель и т.п.) имеет инструкцию по эксплуатации, т.е. словесное описания алгоритма, в соответствии которому данный прибор должен использоваться.

Никаких правил составления словесного описания не существует. Запись алгоритма осуществляется в произвольной форме на естественном, например, русском языке. Этот способ описания не имеет широкого распространения, так как строго не формализуем (под «формальным» понимается то, что описание абсолютно полное и учитывает все возможные ситуации, которые могут возникнуть в ходе решения); допускает неоднозначность толкования при о