Алгоритмическая конструкция «Цикл»

Циклической (или циклом) называют алгоритмическую конструкцию, в которой некая, идущая подряд группа действий (шагов) алгоритма может выполняться несколько раз, в зависимости от входных данных или условия задачи. Группа повторяющихся действий на каждом шагу цикла называется телом цикла. Любая циклическая конструкция содержит в себе элементы ветвящейся алгоритмической конструкции.

Рассмотрим три типа циклических алгоритмов: цикл с параметром (который называют арифметическим циклом), цикл с предусловием и цикл с постусловием (их называют итерационными).

Арифметический цикл

В арифметическом цикле число его шагов (повторений) однозначно определяется правилом изменения параметра, которое задается с помощью начального (N) и конечного (К) значений параметра и шагом (h) его изменения. Т.е., на первом шаге цикла значение па­раметра равно N, на втором - N + h, на третьем - N + 2h и т.д. На последнем шаге цикла значение параметра не больше К, но та­кое, что дальнейшее его изменение приведет к значению, большему, чем К.

Пример 6.4.

Вывести 10 раз слово «Привет!».

Параметр цикла обозначим /, он будет отвечать за количество выведенных слов. При / = 1 будет выведено первое слово, при / = 2 будет выведено второе слова и т.д. Так как требуется вывести 10 слов, то последнее значение параметра / = 10. В заданном примере требу­ется 10 раз повторить одно и то же действие: вывести слово «При-

301вет!». Составим алгоритм, ис­пользуя арифметический цикл, в котором правило изменения параметра / = 1,10,1. Т.е. на­чальное значение параметра /= 1; конечное значение/= 10; шаг изменения И = 1. На рис. 6.7 представлена блок-схема алгоритма решения данной за­дачи.

Привет! J ( Конец J

Рис. 6.7. Блок-схема к примеру 6.4

Цикл с предусловием

Количество шагов цикла заранее не определено и зависит от входных данных задачи. В данной циклической структуре сначала проверяется значение условного выражения (условие) перед выпол­нением очередного шага цикла. Если значение условного выражения истинно, исполняется тело цикла. После чего управление вновь пе­редается проверке условия и т.д. Эти действия повторяются до тех пор, пока условное выражение не примет значение ЛОЖЬ. При пер­вом же несоблюдении условия цикл завершается.

 

 

 

 

 

 

	^^ Условие ^^>	Условие |
	+ |
Да		Тело цикла
	Тело цикла
	а			б

Рис. 6.8. Блок-схема цикла с предусловием

Блок-схема данной конструкции представлена на рис. 6.8'двумя способами: с помощью условного блока а и с помощью блока гра­ницы цикла б.

Особенностью цикла с предусловием является то, что если из­начально условное выражение ложно, то тело цикла не выполнится ни разу.

Пример 6.5.

Одним из наиболее распространенных алгоритмов, встречаю­щихся в литературе по информатике, является алгоритм Евклида -алгоритм нахождения наибольшего общего делителя двух натураль­ных чисел тип (рис.6.9).

Рис. 6.9. Блок-схема алгоритма Евклида

303Опишем его на псевдокоде:

1. Ввод натуральных чисел тип.

2. Пока т t- n делать.

2.1. Если т>п, то т=т — п, иначе п— п — т.

2.2. Переход к шагу 2.

3. Вывод т (найденный наибольший общий делитель).

4. Конец.

Цикл с постусловием

Как и в цикле с предусловием, в циклической конструкции с постусловием заранее не определено число повторений тела цикла, оно зависит от входных данных задачи. В отличие от цикла с пред­условием, тело цикла с постусловием всегда будет выполнено хотя бы один раз, после чего проверяется условие. В этой конструкции тело цикла будет выполняться до тех пор, пока значение условного выражения ложно. Как только оно становится истинным, выполне­ние команды прекращается. Блок-схема данной конструкции пред­ставлена на рис. 6.10 двумя способами: с помощью условного блока а и с помощью блока управления б.

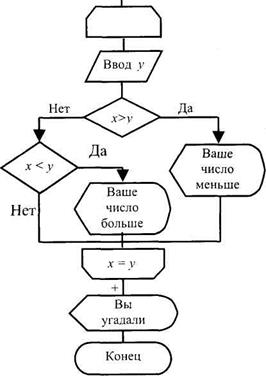
Тело цикла

I

Условие

а

Рис. 6.10. Блок-схема цикла с постусловием

Пример 6.6.

Составим алгоритм игры «Угадай число». Первый игрок вводит задуманное число от 1 до 50. Второй (угадывающий) вводит другое число и получает один из ответов: «Ваше число меньше», «Ваше чис­ло больше» или «Вы угадали». Игра продолжается до тех пор, пока второй игрок не угадает задуманное число.

Составляя алгоритм игры, обозначим х - число, задуманное пер­вым игроком, у — число, вводимое на очередном шаге вторым игро­ком. Блок-схема алгоритма приведена на рис. 6.11.

С Начало J

I / Ввод х /

Рис. 6.11. Блок-схема игры «Угадай число» (пример 6.6)

305Рассмотрим стандартные циклические алгоритмы, такие как вы­числение суммы и подсчет количества элементов, удовлетворяющих некоторому признаку.

Суммирование.

Пример 6.7.

Для заданного натурального числа N вычислить сумму

2 3 N

Подсчет суммы осуществляется следующим образом. Сначала счи- ' таем, что сумма S есть первое слагаемое (S = 1). Далее к первому сла-

1 гаемому прибавляем второе, получаем новую сумму 5 = 1 + —. Но

на предыдущем шаге S = 1, поэтому можно записать S = S + —. к сум­ме двух первых слагаемых прибавляем третье 5 = 1 + — + -. Но на

1 1 предыдущем шагу 5 = 1 + —, поэтому можно записать S = S + - и т.д.

2 3

Получили следующую последовательность шагов: 1) S = 1.

2)

3)

2" 3'

Запишем /-и шаг, опираясь на два предыдущих:

i

Выясним правило изменения номера шага /. В описанной по­следовательности / = 1, 2, 3 и т.д. В сумме N слагаемых, поэтому по­следним значением / будет N. Отсюда нашли правило изменения / = 1, N, 1.

Сверяя инструкции каждого шага, находим, что выражение на первом шаге отличается от других (однотипных). Чтобы оно стало таким как все, в сумму надо добавить S, т.е. записать: S = S + 1 (учи-

1 тываем, что 1 ⁼ 7)- Отсюда для S возникает необходимость задания

начального значения, но такого, чтобы S + 1 = 1 (таким должно быть выражение для / = 1), этим числом является нуль, при сложении с нулем сумма не меняется.

Так как известно число шагов цикла, то для построения алго­ритма используем цикл с параметром /.

Алгоритм на псевдокоде:

1. Ввод N..

2. S = 0. "

3. Для / = 1, N, 1 повторить:

3.1. S =

4. Вывод S.

5. Конец.

Блок-схема алгоритма приведена на рис. 6.12.

Сформулируем правило суммирования:

• начальное значение суммы S = 0;

• в теле некоторой циклической конструкции выполнить команду:

S = S + <слагаемое>.

Упражнения для самостоятельной работы:

Для заданного натурального числа N вычислите суммы N-сла-гаемых:

12 3

1. - + - + - +...; 2 3 4

12 3

2. - + - + - +...; 2 4 6

3073.

sin 1

sin 2

sin3

+ 1 + 2 1+2+3

+...

( Начало J

S = 0

 

s = s + -

( Конец j

Рис. 6.12. Алгоритм вычисления суммы

Подсчет количества элементов. Произведем счет: 1, 2, 3, 4, 5 и т.д., этот процесс является циклическим, так как каждый раз мы со­вершаем одно и то же действие: предыдущее натуральное число уве­личиваем на единицу. Обозначив через К - счетчик искомых эле­ментов, легко получить правило счетчика: К = К + 1 (на очередном шаге цикла). Но при первом подсчете должны получить значение К, равное единице, а до начала счета счетчик должен быть пуст, следо­вательно, начальное значение счетчика равно нулю.

Правило счетчика:

• начальное значение счетчика К = 0;

• в теле некоторой циклической конструкции выполнить команду:

К = К + 1.

Пример 6.8

Задано 20 чисел. Сколько среди них чисел, больших 10? Псевдокод:

1. К = 0 {Счетчик чисел, больших 10}.

2. Повторить 20 раз (для / = 1, 20, 1).

2.1. Ввод числа х.

2.2. Если х > 10, то К = К+ 1.

3. Вывод К.

4. Конец.

Блок-схема алгоритма приведена на рис. 6.13. Замечание: в фигурных скобках {....} принято помещать ком­ментарии к алгоритму.

Рис. 6.13. Алгоритм примера 6.8

309В каждом из рассмотренных выше примеров использовалась одна циклическая конструкция. В реальных задачах может встретиться любое число циклов. Обозначив цикл квадратной скобкой, схематич­но представим варианты взаимного расположения циклов (рис. 6.14).

а - последовательные б — вложенные в - запрещенные

Рис. 6.14. Расположение циклов

Алгоритм любой задачи может быть представлен как комбина­ция представленных выше элементарных алгоритмических структур, поэтому данные конструкции: линейную, ветвящуюся и цикличес­кую, называют базовыми.

Рекурсивный алгоритм

Рекурсивным называется алгоритм, организованный таким образом, что в процессе выполнения команд на каком-либо шаге он прямо или косвенно обращается сам к себе.