
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы алгоритмизации и программированияСодержание книги
Поиск на нашем сайте ТЕМА №11 Основы алгоритмизации и программирования 11.1. Этапы подготовки и решения задач на ЭВМ... 1 11.2. Алгоритмы и способы их описания. 3 Понятие алгоритма. 3 Способы описания алгоритмов. 4 Структурные схемы алгоритмов. 7 11.3. Компиляция и интерпретация программ.. 10 11.4. Стили программирования. 11 Процедурное программирование. 11 Функциональное программирование. 14 Логическое программирование. 15 Объектно-ориентированное программирование. 16 11.5. QBASIC.. 18 11.5.1. Основные понятия алгоритмического языка. 18 11.5.2. Алгоритмизация и программирование на Qbasic. Линейные процессы. 20 11.5.3. Алгоритмизация и программирование на Qbasic. Ветвящиеся процессы. 21 11.5.4. Алгоритмизация и программирование на Qbasic. Циклические процессы.. 23 11.5.5. Алгоритмизация и программирование на Qbasic. Обработка массивов. 25 11.6. Контрольные вопросы.. 27 11.7. Библиографический список. 27
11.1. Этапы подготовки и решения задач на ЭВМ На ЭВМ могут решаться задачи различного характера, например: научно-инженерные; разработки системного программного обеспечения; обучения; управления производственными процессами и т. д. В процессе подготовки и решения на ЭВМ научно -инженерных задач можно выделить следующие этапы: · постановка задачи; · математическое описание задачи; · выбор и обоснование метода решения; · алгоритмизация вычислительного процесса; · составление программы; · отладка программы; · решение задачи на ЭВМ и анализ результатов. В задачах другого класса некоторые этапы могут отсутствовать, например, в задачах разработки системного программного обеспечения отсутствует математическое описание. Перечисленные этапы связаны друг с другом. Например, анализ результатов может показать необходимость внесения изменений в программу; алгоритм или даже в постановку задачи. Для уменьшения числа подобных изменений необходимо на каждом этапе по возможности учитывать требования, предъявляемые последующими этапами. В некоторых случаях связь между различными этапами, например, между постановкой задачи и выбором метода решения, между составлением алгоритма и программированием, может быть настолько тесной, что разделение их становится затруднительным. Постановка задачи. На данном этапе формулируется цель решения задачи и подробно описывается ее содержание. Анализируются характер и сущность всех величин, используемых в задаче, и определяются условия, при которых она решается. Корректность постановки задачи является важным моментом, так как от нее в значительной степени зависят другие этапы. Математическое описание задачи. Настоящий этап характеризуется математической формализацией задачи, при которой существующие соотношения между величинами, определяющими результат, выражаются посредством математических формул. Так формируется математическая модель явления с определенной точностью, допущениями и ограничениями. При этом в зависимости от специфики решаемой задачи могут быть использованы различные разделы математики и других дисциплин. | Математическая модель должна удовлетворять по крайней мере двум требованиям: реалистичности и реализуемости. Под реалистичностью понимается правильное отражение моделью наиболее существенных черт исследуемого явления. Реализуемость достигается разумной абстракцией, отвлечением от второстепенных деталей, чтобы свести задачу к проблеме с известным решением. Условием реализуемости является возможность практического выполнения необходимых вычислений за отведенное время при доступных затратах требуемых ресурсов. Выбор и обоснование метода решения. Модель решения задачи с учетом ее особенностей должна быть доведена до решения при помощи конкретных методов решения. Само по себе математическое описание задачи в большинстве случаев трудно перевести на язык машины. Выбор и использование метода решения задачи позволяет привести решение задачи к конкретным машинным операциям. При обосновании выбора метода необходимо учитывать различные факторы и условия, в том числе точность вычислений, время решения задачи на ЭВМ, требуемый объем памяти и другие. Одну и ту же задачу можно решить различными методами, при этом в рамках каждого метода можно составить различные алгоритмы. Алгоритмизация вычислительного процесса. На данном этапе составляется алгоритм решения задачи согласно действиям, задаваемым выбранным методом решения. Процесс обработки данных разбивается на отдельные относительно самостоятельные блоки, и устанавливается последовательность выполнения блоков. Разрабатывается блок-схема алгоритма. Составление программы. При составлении программы алгоритм решения задачи переводится на конкретный язык программирования. Для программирования обычно используются языки высокого уровня, поэтому составленная программа требует перевода ее на машинный язык ЭВМ. После такого перевода выполняется уже соответствующая машинная программа. Отладка программы. Отладка заключается в поиске и устранении синтаксических и логических ошибок в программе. В ходе синтаксического контроля программы транслятором выявляются конструкции и сочетания символов, недопустимые с точки зрения правил их построения или написания, принятых в данном языке. Сообщения об ошибках ЭВМ выдает программисту, при этом вид и форма выдачи подобных сообщений зависят от вида языка и версии используемого транслятора. После устранения синтаксических ошибок проверяется логика работы программы в процессе ее выполнения с конкретными исходными данными. Для этого используются специальные методы, например, в программе выбираются контрольные точки, для которых вручную рассчитываются промежуточные результаты. Эти результаты сверяются со значениями, получаемыми ЭВМ в данных точках при выполнении отлаживаемой программы. Кроме того, для поиска ошибок могут быть использованы отладчики, выполняющие специальные действия на этапе отладки, например, удаление, замена или вставка отдельных операторов или целых фрагментов программы, вывод или изменение значений заданных переменных. Решение задачи на ЭВМ и анализ результатов. После отладки программы ее можно использовать для решения прикладной задачи. При этом обычно выполняется многократное решение задачи на ЭВМ для различных наборов исходных данных. Получаемые результаты интерпретируются и анализируются специалистом или пользователем, поставившим задачу. Разработанная программа длительного использования устанавливается на ЭВМ, как правило, в виде готовой к выполнению машинной программы. К программе прилагается документация, включая инструкцию для пользователя. Чаще всего при установке программы на диск для ее последующего использования помимо файлов с исполняемым кодом устанавливаются различные вспомогательные программы (утилиты, справочники, настройщики и т. д.), а также необходимые для работы программ разного рода файлы с текстовой, графической, звуковой и другой информацией. Алгоритмы и способы их описания Понятие алгоритма Для составления программы, предназначенной для решения на ЭВМ какой-либо задачи, требуется составление алгоритма ее решения. Алгоритм — это точное предписание, которое определяет процесс, ведущий от исходных данных к требуемому конечному результату. Алгоритмами, например, являются правила сложения, умножения, решения алгебраических уравнений, умножения матриц и т.п. Слово алгоритм происходит от algoritmi, являющегося латинской транслитерацией арабского имени хорезмийского математика IX века аль-Хорезми. Благодаря латинскому переводу трактата аль-Хорезми европейцы в XII веке познакомились с позиционной системой счисления, и в средневековой Европе алгоритмом называлась десятичная позиционная система счисления и правила счета в ней. Применительно к ЭВМ алгоритм определяет вычислительный процесс, начинающийся с обработки некоторой совокупности возможных исходных данных и направленный на получение определенных этими исходными данными результатов. Термин вычислительный процесс распространяется и на обработку других видов информации, например, символьной, графической или звуковой. Если вычислительный процесс заканчивается получением результатов, то говорят, что соответствующий алгоритм применим к рассматриваемой совокупности исходных данных. В противном случае говорят, что алгоритм неприменим к совокупности исходных данных. Любой применимый алгоритм обладает следующими основными свойствами: · результативностью; · определенностью; · массовостью. Результативность означает возможность получения результата после выполнения конечного количества операций. Определенность состоит в совпадении получаемых результатов независимо от пользователя и применяемых технических средств. Массовость заключается в возможности применения алгоритма к целому классу однотипных задач, различающихся конкретными значениями исходных данных. Для задания алгоритма необходимо описать следующие его элементы: · набор объектов, составляющих совокупность возможных исходных данных, промежуточных и конечных результатов; · правило начала; · правило непосредственной переработки информации (описание последовательности действий); · правило окончания; · правило извлечения результатов. Алгоритм всегда рассчитан на конкретного исполнителя. В нашем случае таким исполнителем является ЭВМ. Для обеспечения возможности реализации на ЭВМ алгоритм должен быть описан на языке, понятном компьютеру, то есть на языке программирования. Таким образом, можно дать следующее определение программы. Программа для ЭВМ представляет собой описание алгоритма и данных на некотором языке программирования, предназначенное для последующего автоматического выполнения. Способы описания алгоритмов К основным способам описания алгоритмов можно отнести следующие: · словесно-формульный; · структурный или блок-схемный; · с помощью граф-схем; · с помощью сетей Петри. Перед составлением программ чаще всего используются словесно-формульный и блок-схемный способы. Иногда перед составлением программ на низкоуровневых языках программирования типа языка Ассемблера алгоритм программы записывают, пользуясь конструкциями некоторого высокоуровнего языка программирования. Удобно использовать программное описание алгоритмов функционирования сложных программных систем. Так, для описания принципов функционирования ОС использовался Алголоподобный высокоуровневый язык программирования. При словесно-формульном способе алгоритм записывается в виде текста с формулами по пунктам, определяющим последовательность действий. Пусть, например, необходимо найти значение следующего выражения: у = 2а – (х+6). Словесно-формульным способом алгоритм решения этой задачи может быть записан в следующем виде: 1. Ввести значения а и х. 2. Сложить х и 6. 3. Умножить a на 2. 4. Вычесть из 2а сумму (х+6). 5. Вывести у как результат вычисления выражения. При блок-схемном описании алгоритм изображается геометрическими фигурами (блоками), связанными по управлению линиями (направлениями потока) со стрелками. В блоках записывается последовательность действий. Данный способ по сравнению с другими способами записи алгоритма имеет ряд преимуществ. Он наиболее нагляден: каждая операция вычислительного процесса изображается отдельной геометрической фигурой. Кроме того, графическое изображение алгоритма наглядно показывает разветвления путей решения задачи в зависимости от различных условий, повторение отдельных этапов вычислительного процесса и Другие детали. Оформление программ должно соответствовать определенным требованиям. В настоящее время действует единая система программной документации (ЕСПД), которая устанавливает правила разработки, оформления программ и программной документации. В ЕСПД определены и правила оформления блок-схем алгоритмов (ГОСТ 10.002-80 ЕСПД, ГОСТ 10.003-80 ЕСПД). Операции обработки данных и носители информации изображаются на схеме соответствующими блоками. Большая часть блоков по построению условно вписана в прямоугольник со сторонами а и b. Минимальное значение а = 10 мм, увеличение а производится на число, кратное 5 мм. Размер b=1,5a. Для от дельных блоков допускается соотношение между а и b, равное 1:2. В пределах одной схемы рекомендуется изображать блоки одинаковых размеров. Все блоки нумеруются. Виды и назначение основных блоков приведены в табл. 1.
Таблица 1. Условные обозначения блоков схем алгоритмов
Линии, соединяющие блоки и указывающие последовательность связей между ними, должны проводится параллельно линиям рамки. Стрелка в конце линии может не ставиться, если линия направлена слева направо или сверху вниз. В блок может входить несколько линий, то есть блок может являться преемником любого числа блоков. Из блока (кроме логического) может выходить только одна линия. Логический блок может иметь в качестве продолжения один из двух блоков, и из него выходят две линии. Если на схеме имеет место слияние линий, то место пересечения выделяется точкой. В случае, когда одна линия подходит к другой и слияние их явно выражено, точку можно не ставить. Схему алгоритма следует выполнять как единое целое, однако в случае необходимости допускается обрывать линии, соединяющие блоки. Если при обрыве линии продолжение схемы находится на этом же листе, то на одном и другом конце линии изображается специальный символ соединитель — окружность диаметром 0,5 а. Внутри парных окружностей указывается один и тот же идентификатор. В качестве идентификатора, как правило, используется порядковый номер блока, к которому направлена соединительная линия. Если схема занимает более одного листа, то в случае разрыва линии вместо окружности используется межстраничный соединитель. Внутри каждого, соединителя указывается адрес — откуда и куда направлена соединительная линия. Адрес записывается в две строки: в первой указывается номер листа, во второй — порядковый номер блока. Блок-схема должна содержать все разветвления, циклы и обращения к подпрограммам, содержащиеся в программе. Стили программирования Одним из важнейших признаков классификации языков программирования является принадлежность их к одному из стилей, основными из которых являются следующие: процедурный, функциональный, логический и объектно-ориентированный. Логическое программирование Новую область — логическое, или реляционное программирование, — открыло появление языка PROLOG (Пролог) (PROgramming in LOGic — программирование в терминах логики). Этот язык был создан французским ученым А. Кольмероэ в 1973 году. В настоящее время известны и другие языки, однако наиболее развитым и распространенным языком логического программирования является именно Пролог. Так, имеется свыше 15 различных его реализаций на ПЭВМ. Языки логического программирования, в особенности Пролог, широко используются в системах искусственного интеллекта, рассматриваемых в данном учебном пособии. Центральным понятием в логическом программировании является отношение. Программа представляет собой совокупность определений отношений между объектами (в терминах условий или ограничений) и цели (запроса). Процесс выполнения программы трактуется как процесс общезначимости логической формулы, построен- ной из программы по правилам, установленным семантикой используемого языка. Результат вычисления является побочным продуктом этого процесса. В реляционном программировании нужно только специфицировать факты, на которых алгоритм основывается, а не определять последовательность шагов, которые требуется выполнить. Это свидетельствует о декларативности языка логического программирования. Она метко выражена в формуле Р. Ковальского: «алгоритм = логика + управление». Языки логического программирования характеризуются: · высоким уровнем; · строгой ориентацией на символьные вычисления; · возможностью инверсных вычислений, то есть переменные в процедурах не делятся на входные и выходные; · возможной логической неполнотой, поскольку зачастую невозможно выразить в программе определенные логические соотношения, а также невозможно получить из программы все выводы правильные. Логические программы, в принципе, имеют небольшое быстродействие, так как вычисления осуществляются методом проб и ошибок, поиском с возвратами к предыдущим шагам. Основные понятия алгоритмического языка. Этапы подготовки задачи к решению на компьютере: -Постановка задачи (процесс построения математической модели) -Алгоритмизация (процесс построения алгоритма решения задачи) -Программирование (процесс записи алгоритма на языке программирования) -Отладка программы (процесс исправления ошибок и проверки работы программы). Линейные процессы. Линейным называется такой вычислительный процесс, при котором все этапы решения задачи выполняются в естественном порядке следования записи этих этапов. НЕКОТОРЫЕ ЛИНЕЙНЫЕ ОПЕРАТОРЫ INPUT – оператор ввода данных с клавиатуры, имена переменных в списке разделяют запятыми. [LET] – оператор присваивания, переменная = выражение PRINT – оператор вывода данных на экран, выражения в списке разделяются либо запятой, либо точкой с запятой. END – оператор окончания программы. Задача №1 Найти и вывести результат вычисления выражения: РЕШЕНИЕ АЛГОРИТМ ПРОГРАММА НА QBASIC
REM программа решения задачи 1
PRINT “y=”; y END
Ветвящиеся процессы. Ветвящимся называется такой вычислительный процесс, в котором выбор направления обработки информации зависит от исходных или промежуточных данных.
АЛГОРИТМЫ ВЕТВЯЩИХСЯ процессов ПОЛНАЯ ФОРМА. СОКРАЩЕННАЯ ФОРМА
НЕКОТОРЫЕ ЛИНЕЙНЫЕ ОПЕРАТОРЫ IF…THEN…ELSE – оператор ветвления, изменяет ход выполнения программы в зависимости от результата проверки условий. (опера тор «если… то…иначе»)
ПОЛНАЯ ФОРМА. СОКРАЩЕННАЯ ФОРМА ЛИНЕЙНАЯ: IF условие THEN оператор 1 ELSE оператор 2 IF условие THEN оператор 1 БЛОЧНАЯ IF условие THEN IF условие THEN оператор 1 оператор 1 ELSE END IF оператор 2 END IF Задача №2 Найти и вывести результат вычисления выражения: РЕШЕНИЕ АЛГОРИТМ ПРОГРАММА НА QBASIC
REM программа решения задачи 2
IF a-b<>0 THEN y=(a^2+b)/(a-b) PRINT “y=”; y
Циклические процессы Циклом называется многократно повторяемый участок вычислений.
АЛГОРИТМЫ ЦИКЛИЧЕСКИХ процессов
ЦИКЛ С ПРЕДУСЛОВИЕМ ЦИКЛ С ПОСТУСЛОВИЕМ

ДА НЕТ
НЕТ
НЕКОТОРЫЕ ЦИКЛИЧЕСКИЕ ОПЕРАТОРЫ FOR…NEXT – оператор цикла, организует в программе циклическое выполнение группы операторов заданное число раз
FOR переменная = начало TO конец [STEP шаг ] Оператор тела цикла NEXT [переменная] Задача №3 Найти и вывести результат вычисления выражения: РЕШЕНИЕ АЛГОРИТМ ПРОГРАММА НА QBASIC
REM программа решения задачи 3 INPUT «введите число b»; b FOR a = -4 TO 8 STEP 2 y=(a+b)^2/(1+a^2) PRINT y NEXT a END
ДА
НЕТ
Обработка массивов. Массивом называется совокупность элементов с одинаковыми свойствами. Любой массив характеризуется именем, размерностью, типом элементов. Массивы могут быть одномерные, двумерные и т.д. Обработка любого массива представляет собой циклический вычислительный процесс, в котором параметры индексов являются индексы. Линейные массивы. Массив с одним индексом называется вектором или линейным массивом. оператор массива dim DIM – оператор объявляет массивы и переменные, резервирует объем памяти для записи всех элементов массива и переменных. DIM имя массива (границы) [имя массива (границы)…] Одномерный массив называется вектором, обозначается: А(i), где i – номер элемента. Задача №4 Найти и вывести сумму элементов массива А, состоящего из 5 элементов. РЕШЕНИЕ АЛГОРИТМ ПРОГРАММА НА QBASIC
REM программа решения задачи 4
INPUT «введите A(I)»; A(I)
S = 0
S = S + A(I)
PRINT S Д
НЕТ
11.6. Контрольные вопросы 1. Дайте классификацию видов ПО. 2. Назовите этапы подготовки и решения задач на ЭВМ. 3. Что такое алгоритм и какими свойствами он обладает? 4. Укажите способы описания и виды алгоритмов. 5. Что такое компиляция и интерпретация программ? 6. Охарактеризуйте основные стили программирования. 7. Характерные свойства языка программирования Qbasic. 8. Операторы линейных, разветвляющихся и циклических процессов в Qbasic. Библиографический список 1. Аверьянов Г.Я., Рошаль А. С. Элементы информатики: Учебное пособие.— М.:МИФИ, 1995.-175 с. 2. Богумирский Б. С. Руководство пользователя ПЭВМ: в 2-х частях,—Санкт-Петербург: Ассоциация OILCO, 1992. - 735 с. 3. ГОСТ 19.002-80 ЕСПД. 4. ГОСТ 19.003-80 ЕСПД. 5. Дворкин П. Л. Основы информатики и вычислительной техники: Учебное пособие.— Омск.: ОПИ, 1988. -119с. 6. Иванов Н. C++ или Java // Мир Internet, № 1,1997. - С. 42-49. 7. Информатика* Энциклопедический словарь для начинающих/Сост. Д. А. Поспелов — М.: Педагогика — Пресс, 1994. — 352 с. 8. Компьютерные технологии обработки информации: Учебное пособие /С. В. Назаров, В. И. Першинов, В. А. Тафинцев и др.; Под ред. С. В. Назарова. — М.: Финансы и статистика, 1995. — 248 с. 9. Основные понятия информатики и вычислительной техники: Методические материалы. — Новосибирск, 1990. — 123 с. 10. Основы компьютерной грамоты / А. Н.Жигарев, Н. В. Макарова, М. А. Путинце-ва; Под общ. ред. Н. В. Макаровой. — Л.: Машиностроение, 1987. — 255 с. 11. Программирование. Учебник под ред. Свердлика А. Н., МО СССР, 1992. — 608 с. 12. Ростовцев Ю. Г. Основы построения автоматизированных систем сбора и обработки информации: Учебник. — СПб.: ВИККА им. А. Ф. Можайского, 1992. — 717 с. 13. Трудов Ю. В. Основы построения ЭВМ. Часть 1. Теоретические основы, элементы и узлы ЭВМ: Учебное пособие. - Л.: ВИКИ им. А. Ф. Можайского, 1990. - 216 с. 14. Шафрин Ю. А. Основы компьютерных технологий. Уч. Пособие для 7-11 классов по курсу «Информатика и вычислительная техника». — М.: ABF, 1996. ~ 560 с. 15. Шоу А. Логическое проектирование операционных систем: Пер. с англ. — М.: Мир, 1981.-360 с.
ТЕМА №11 Основы алгоритмизации и программирования 11.1. Этапы подготовки и решения задач на ЭВМ... 1 11.2. Алгоритмы и способы их описания. 3 Понятие алгоритма. 3 Способы описания алгоритмов. 4 Структурные схемы алгоритмов. 7 11.3. Компиляция и интерпретация программ.. 10 11.4. Стили программирования. 11 Процедурное программирование. 11 Функциональное программирование. 14 Логическое программирование. 15 Объектно-ориентированное программирование. 16 11.5. QBASIC.. 18 11.5.1. Основные понятия алгоритмического языка. 18 11.5.2. Алгоритмизация и программирование на Qbasic. Линейные процессы. 20 11.5.3. Алгоритмизация и программирование на Qbasic. Ветвящиеся процессы. 21 11.5.4. Алгоритмизация и программирование на Qbasic. Циклические процессы.. 23 11.5.5. Алгоритмизация и программирование на Qbasic. Обработка массивов. 25 11.6. Контрольные вопросы.. 27 11.7. Библиографический список. 27
11.1. Этапы подготовки и решения задач на ЭВМ На ЭВМ могут решаться задачи различного характера, например: научно-инженерные; разработки системного программного обеспечения; обучения; управления производственными процессами и т. д. В процессе подготовки и решения на ЭВМ научно -инженерных задач можно выделить следующие этапы: · постановка задачи; · математическое описание задачи; · выбор и обоснование метода решения; · алгоритмизация вычислительного процесса; · составление программы; · отладка программы; · решение задачи на ЭВМ и анализ результатов. В задачах другого класса некоторые этапы могут отсутствовать, например, в задачах разработки системного программного обеспечения отсутствует математическое описание. Перечисленные этапы связаны друг с другом. Например, анализ результатов может показать необходимость внесения изменений в программу; алгоритм или даже в постановку задачи. Для уменьшения числа подобных изменений необходимо на каждом этапе по возможности учитывать требования, предъявляемые последующими этапами. В некоторых случаях связь между различными этапами, например, между постановкой задачи и выбором метода решения, между составлением алгоритма и программированием, может быть настолько тесной, что разделение их становится затруднительным. Постановка задачи. На данном этапе формулируется цель решения задачи и подробно описывается ее содержание. Анализируются характер и сущность всех величин, используемых в задаче, и определяются условия, при которых она решается. Корректность постановки задачи является важным моментом, так как от нее в значительной степени зависят другие этапы. Математическое описание задачи. Настоящий этап характеризуется математической формализацией задачи, при которой существующие соотношения между величинами, определяющими результат, выражаются посредством математических формул. Так формируется математическая модель явления с определенной точностью, допущениями и ограничениями. При этом в зависимости от специфики решаемой задачи могут быть использованы различные разделы математики и других дисциплин. | Математическая модель должна удовлетворять по крайней мере двум требованиям: реалистичности и реализуемости. Под реалистичностью понимается правильное отражение моделью наиболее существенных черт исследуемого явления. Реализуемость достигается разумной абстракцией, отвлечением от второстепенных деталей, чтобы свести задачу к проблеме с известным решением. Условием реализуемости является возможность практического выполнения необходимых вычислений за отведенное время при доступных затратах требуемых ресурсов. Выбор и обоснование метода решения. Модель решения задачи с учетом ее особенностей должна быть доведена до решения при помощи конкретных методов решения. Само по себе математическое описание задачи в большинстве случаев трудно перевести на язык машины. Выбор и использование метода решения задачи позволяет привести решение задачи к конкретным машинным операциям. При обосновании выбора метода необходимо учитывать различные факторы и условия, в том числе точность вычислений, время решения задачи на ЭВМ, требуемый объем памяти и другие. Одну и ту же задачу можно решить различными методами, при этом в рамках каждого метода можно составить различные алгоритмы. Алгоритмизация вычислительного процесса. На данном этапе составляется алгоритм решения задачи согласно действиям, задаваемым выбранным методом решения. Процесс обработки данных разбивается на отдельные относительно самостоятельные блоки, и устанавливается последовательность выполнения блоков. Разрабатывается блок-схема алгоритма. Составление программы. При составлении программы алгоритм решения задачи переводится на конкретный язык программирования. Для программирования обычно используются языки высокого уровня, поэтому составленная программа требует перевода ее на машинный язык ЭВМ. После такого перевода выполняется уже соответствующая машинная программа. Отладка программы. Отладка заключается в поиске и устранении синтаксических и логических ошибок в программе. В ходе синтаксического контроля программы транслятором выявляются конструкции и сочетания символов, недопустимые с точки зрения правил их построения или написания, принятых в данном языке. Сообщения об ошибках ЭВМ выдает программисту, при этом вид и форма выдачи подобных сообщений зависят от вида языка и версии используемого транслятора. После устранения синтаксических ошибок проверяется логика работы программы в процессе ее выполнения с конкретными исходными данными. Для этого используются специальные методы, например, в программе выбираются контрольные точки, для которых вручную рассчитываются промежуточные результаты. Эти результаты сверяются со значениями, получаемыми ЭВМ в данных точках при выполнении отлаживаемой программы. Кроме того, для поиска ошибок могут быть использованы отладчики, выполняющие специальные действия на этапе отладки, например, удаление, замена или вставка отдельных операторов или целых фрагментов программы, вывод или изменение значений заданных переменных. Решение задачи на ЭВМ и анализ результатов. После отладки программы ее можно использовать для решения прикладной задачи. При этом обычно выполняется многократное решение задачи на ЭВМ для различных наборов исходных данных. Получаемые результаты интерпретируются и анализируются специалистом или пользователем, поставившим задачу. Разработанная программа длительного использования устанавливается на ЭВМ, как правило, в виде готовой к выполнению машинной программы. К программе прилагается документация, включая инструкцию для пользователя. Чаще всего при установке программы на диск для
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1059; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.019 с.) |













 INPUT a, b
INPUT a, b y=(a^2-b)/50
y=(a^2-b)/50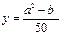



 ДА НЕТ ДА НЕТ
ДА НЕТ ДА НЕТ






 INPUT a, b
INPUT a, b ДА НЕТ ELSE
ДА НЕТ ELSE PRINT “Решения нет”
PRINT “Решения нет”
 END
END




 ДА
ДА
 при aÎ(-4;8) с шагом 2.
при aÎ(-4;8) с шагом 2.
 DIM A(5)
DIM A(5) NEXT I
NEXT I
 FOR I = 1 TO 5
FOR I = 1 TO 5 A END
A END


 ДА
ДА




