Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Структурные схемы алгоритмовСодержание книги
Поиск на нашем сайте
Одним из свойств алгоритма является дискретность — возможность расчленения процесса вычислений, предписанных алгоритмом, на отдельные этапы, возможность выделения участков программы с определенной структурой. Можно выделить и наглядно представить графически три простейшие структуры: · последовательность двух или более операций; · выбор направления; · повторение. Любой вычислительный процесс может быть представлен как комбинация этих элементарных алгоритмических структур. Соответственно, вычислительные процессы, выполняемые на ЭВМ по заданной программе, можно разделить на три основных вида: · линейные; · ветвящиеся; · циклические. Линейным принятоназывать вычислительный процесс, в котором операции выполняются последовательно, в порядке их записи. Каждая операция является самостоятельной, независимой от каких-либо условий. На схеме блоки, отображающие эти операции, располагаются в линейной последовательности. Линейные вычислительные процессы имеют место, например, при вычислении арифметических выражений, когда имеются конкретные числовые данные и над ними выполняются соответствующие условию задачи действия. На рис. 11.1, а показан пример линейного алгоритма, определяющего процесс вычисления арифметического выражения у=(b2-ас):(а+с).
Рис. 11.1. Примеры алгоритмов: а) линейный алгоритм; б) ветвящийся алгоритм Вычислительный процесс называется ветвящимся, если для его реализации предусмотрено несколько направлений (ветвей). Каждое отдельное направление процесса обработки данных является отдельной ветвью вычислений. Ветвление в программе — это выбор одной из нескольких последовательностей команд при выполнении программы. Выбор направления зависит от заранее определенного признака, который может относиться к исходным данным, к промежуточным или конечным результатам. Признак характеризует свойство данных и имеет два или более значений. Ветвящийся процесс, включающий в себя две ветви, называется простым, более двух ветвей — сложным. Сложный ветвящийся процесс можно представить с помощью простых ветвящихся процессов. Направление ветвления выбирается логической проверкой, в результате которой возможны два ответа: «да» — условие выполнено и «нет» — условие не выполнено.
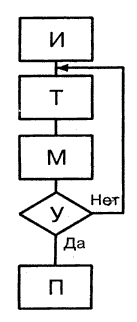
Следует иметь в виду, что, хотя на схеме алгоритма должны быть показаны все возможные направления вычислений в зависимости от выполнения определенного условия (или условий), при однократном прохождении программы процесс реализуется только по одной ветви, а остальные исключаются. Любая ветвь, по которой осуществляются вычисления, должна приводить к завершению вычислительного процесса. На рис. 11.1,б показан пример алгоритма с разветвлением для вычисления следующего выражения: Y = (а+b), если Х <0; с/b, если Х>0. Циклическими называются программы, содержащие циклы. Цикл — это многократно повторяемый участок программы. В организации цикла можно выделить следующие этапы: · • подготовка (инициализация) цикла (И); · • выполнение вычислений цикла (тело цикла) (Т); · • модификация параметров (М); · • проверка условия окончания цикла (У). Порядок выполнения этих этапов, например, Т и М, может изменяться. В зависимости от расположения проверки условия окончания цикла различают циклы с нижним и верхним окончаниями (рис. 11.2). Для цикла с нижним окончанием (рис. 11.2, а) тело цикла выполняется как минимум один раз, так как сначала производятся вычисления, а затем проверяется условие выхода из цикла. В случае цикла с верхним окончанием (рис. 11.2, б) тело цикла может не выполниться ни разу в случае, если сразу соблюдается условие выхода.
Рис. 11.2. Примеры циклических алгоритмов Цикл называется детерминированным, если число повторений тела цикла заранее известно или определено. Цикл называется итерационным, если число повторений тела цикла заранее неизвестно, а зависит от значений параметров (некоторых переменных), участвующих в вычислениях. На рис. 11.3 показан пример циклического алгоритма вычисления суммы десяти чисел.
Рис. 11.3. Алгоритм нахождения суммы 10-ти чисел
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 331; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.137.244 (0.006 с.) |