Формализация алгоритма. Абстрактные автоматы

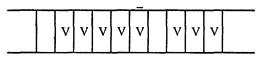
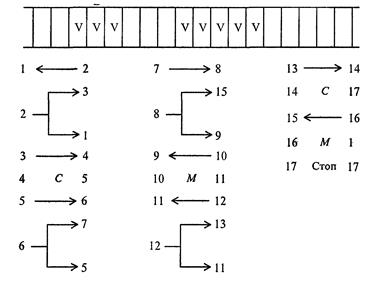
Алгоритмы являются объектом систематического исследования пограничной между математикой и информатикой научной дисциплины, примыкающей к математической логике, – теории алгоритмов.

Как фундаментальное научное понятие алгоритм требует более обстоятельного изучения. Оно невозмож­но без уточнения понятия “алгоритм”, более строгого его описания или, как еще говорят, без его формализации.

Одним из подходов к формализации понятия “алгоритм” является теория конечных и бесконечных автоматов.

Рассмотрим формализацию понятия алгоритма в теории автоматов на примере машин Поста, Тьюринга, а также нормальных алгоритмов Маркова.

Машина Поста. Абстрактные (т.е. существующие не реально, а лишь в воображении) машины Поста и Тьюринга, предназначенные для доказательств различных утверждений о свойствах программ для них, были предложены независимо друг от друга (и прак­тически одновременно) в 1936 г. американским математиком Эмилем Постом и английским математиком Алланом Тьюрингом. Эти машины представляют собой универсальных исполнителей, являющихся полностью детерминированными, позволяющих “вводить” начальные данные и после выполнения программ “читать” результат. Машина Поста менее популярна, хотя она значительно проще машины Тьюринга.

Абстрактная машина Поста представляет собой бесконечную ленту, разделен­ную на одинаковые клетки, каждая из которых может быть либо пустой, либо заполненной меткой “V”, и головку, которая может перемещаться вдоль ленты на одну клетку вправо или влево, наносить в клетку ленты метку, если этой метки там ранее не было, стирать метку, если она была, или проверять наличие в клетке метки. Информация о заполненных метками клетках ленты характеризует состояние ленты, которое может меняться в процессе работы машины. В каждый момент времени головка (“–”) находится над одной из клеток ленты и, как говорят, обозре­вает ее. Информация о местоположения головки вместе с состоянием ленты харак­теризует состояние машины Поста (рис. 3.1).

Рис. 3.1. Абстрактная машина Поста

Команда машины Поста имеет следующую структуру:

n Km,

где n – порядковый номер команды, K-действие, выполняемое головкой, m- номер следующей команды, подлежащей выполнению.

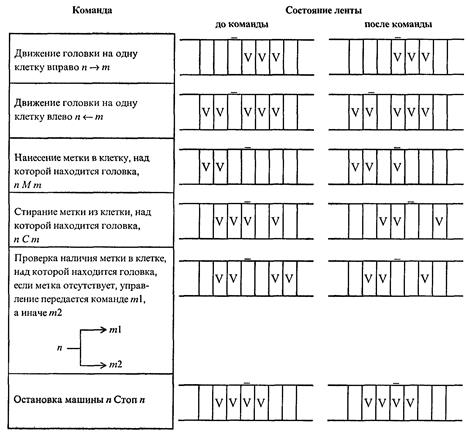
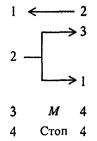
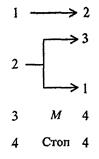
Существует всего шесть команд машины Поста (рис. 3.2).

Ситуации, в которых головка должна наносить метку там, где она уже имеется, или, наоборот, стирать метку там, где ее нет, являются аварийными (недопустимыми).

Программой для машины Поста будем называть непустой список команд, такой что:

1) на n-м месте команда с номером n;

2) номер m каждой команды совпадает с номером какой-либо команды списка.

С точки зрения свойств алгоритмов, изучаемых с помощью машины Поста, наи­больший интерес представляют причины останова машины при выполнении программы:

1) останов по команде “стоп”; такой останов называется результативным и ука­зывает на корректность алгоритма (программы);

2) останов при выполнении недопустимой команды; в этом случае останов назы­вается безрезультативным;

3) машина не останавливается никогда; в этом и в предыдущем случае мы имеем дело с некорректным алгоритмом (программой).

 

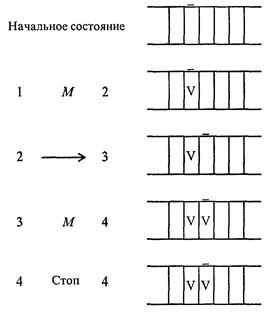
Рис. 3.2. Команды машины Поста

Будем понимать под начальным состояние головки против пустой клетки левее самой левой метки на ленте.

Рассмотрим реализацию некоторых типичных элементов программ машины Поста.

1. Пусть задано исходное состояние головки и требуется на пустой ленте написать две метки: одну в секцию под головкой, вторую справа от нее. Это можно сделать по следующей программе (справа от команды показан результат ее выполнения) (рис. 3.3):

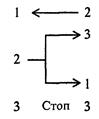
Рис. 3.3. Пример элемента программы машины Поста

2. Покажем, как можно воспользоваться командой условного перехода для ор­ганизации циклического процесса. Пусть на ленте имеется запись из нескольких меток подряд и головка находится над самой крайней меткой справа. Требуется перевести головку влево до первой пустой позиции.

Программа будет иметь следующий вид:

Команда условного перехода является одним из основных средств организации циклических процессов, например, для нахождения первой метки справа (или слева) от головки, расположенной над пустой клеткой; нахождение слева (или справа) от головки пустой клетки, если она расположена над меткой и т.д.

3. Остановимся на представлении чисел на ленте машины Поста и выполнении операций над ними.

Число k представляется на ленте машины Поста идущими подряд k + 1 метками (одна метка означает число “0”). Между двумя числами делается интервал как минимум из одной пустой секции на ленте. Например, запись чисел 3 и 5 на ленте машины Поста будет выглядеть так:

 

Используемая в машине Поста система записи чисел яв­ляется непозиционной.

Составим программу для прибавления к произвольному числу единицы. Пред­положим, что на ленте записано только одно число и головка находится над одной из клеток, в которой находится метка, принадлежащая этому числу:

Для решения задачи нужно добавить одну метку с любой стороны. Ее можно добавить, переместив головку влево (или вправо) до первой пустой клетки, а затем нанести метку.

Программа, добавляющая к числу метку слева, имеет вид:

Программа, добавляющая к числу метку справа, имеет вид:

4. Приведем программу для сложения целых неотрицательных чисел a и b на ма­шине Поста, когда головка находится над числом a, а число b находится правее числа а на некоторое число клеток. Эта программа реализует следующий алгоритм: первое число постепенно придвигается ко второму до их слияния, а потом стирается одна метка (иначе результат оказался бы на единицу больше правильного).

Машину Поста можно рассматривать как упрощенную модель ЭВМ. В самом деле, как ЭВМ, так и машина Поста имеют:

· неделимые носители информации (клетки – биты), которые могут быть за­полненными или незаполненными;

· ограниченный набор элементарных действий – команд, каждая из которых выполняется за один такт (шаг).

Обе машины работают на основе программы. Однако в машине Поста инфор­мация располагается линейно и читается подряд, а в ЭВМ можно читать информа­цию по адресу; набор команд ЭВМ значительно шире и выразительнее, чем коман­ды машины Поста, и т.д.

Машина Тьюринга. Машина Тьюринга подобна машине Поста, но функционирует несколько иначе.

Машина Тьюринга (МТ) состоит из счетной ленты (разделенной на ячейки и ограниченной слева, но не справа), читающей и пишущей головки, лентопротяжно­го механизма и операционного исполнительного устройства, которое может находиться в одном из дискретных состояний q0,q1,...,qs, принадлежащих некото­рой конечной совокупности (алфавиту внутренних состояний). При этом q0 называ­ется начальным состоянием.

Читающая и пишущая головка может читать буквы рабочего алфавита А=[а0,а1,...,аt}, стирать их и печатать. Каждая ячейка ленты в каждый момент времени занята буквой из множества А. Чаще всего встречается буква a0 – “пробел”. Головка находится в каждый момент времени над некоторой ячейкой ленты – текущей рабочей ячейкой. Лентопротяжный механизм может перемещать ленту так, что головка оказывается над соседней ячейкой ленты. При этом возможна ситуация выхода за левый край ленты (ЛК), которая является аварийной (недопустимой), или машинного останова (МО), когда машина выполняет предписание об остановке.

Порядок работы МТ (с рабочим алфавитом а0,а1,...,аt и состояниями q0,q1,...,qs) описывается таблицей машины Тьюринга. Эта таблица является матрицей с че­тырьмя столбцами и (s+1)(t+1) строками. Каждая строка имеет вид:

qi aj vij qij, где 0 £ I £ s, 0 £ j £ t, qij Î{q0,q1,...,qs}.

Здесь через vij обозначен элемент объединения алфавита {а0,а1,...,аt} и множест­ва предписаний для лентопротяжного механизма: g – переместить ленту влево, r -переместить ленту вправо, s – остановить машину; vij – действие МТ, состоящее либо в занесении в ячейку ленты символа алфавита а0,а1,...,аt, либо в движении головки, либо в останове машины; qij является последующим состоянием.

МТ работает согласно следующим правилам: если МТ находится в состоянии qi, головка прочитывает символ aj в рабочей ячейке. Пусть строка qi aj vij qij, начинаю­щаяся с символов qi aj, встречается только один раз в таблице. Если vij – буква рабочего алфавита, то головка стирает содержимое рабочей ячейки и заносит туда эту букву. Если vij – команда r или g для лентопротяжного механизма, то лента сдвигается на одну ячейку вправо или влево (если не происходит выхода за левый край ленты) соответственно. Если vij = s, то происходит машинный останов.

Машина Тьюринга начинает работу из некоторой начальной конфигурации, включающей в себя начальное состояние (обычно q0) и положение считывающе-записывающей головки над определенной ячейкой ленты, содержащей один из символов рабочего алфавита А.

Наличие разнообразных символов в рабочем алфавите МТ позволяет представлять на ленте произвольную текстовую и числовую информацию, а переходы управляющего центра МТ в различные состояния моделируют запоминание машиной Тьюринга промежуточных результатов работы. Таблица, определяющая порядок работы МТ, не является в прямом смысле слова программой (ее предписания выпол­няются не последовательно, одно за другим, а описывают преобразования символов некоторого текста, находящегося на ленте). Таблицу МТ часто называют схемой машины Тьюринга или попросту отождествляют с самой машиной Тьюринга.

Рассмотрим примеры нескольких схем машины Тьюринга.

1. Алгоритм прибавления единицы к числу n в десятичной системе счисления.

Дана десятичная запись числа n (т.е. представление натурального числа n в деся­тичной системе счисления); требуется получить десятичную запись числа n+1.

Очевидно, что внешний алфавит МТ должен состоять из десяти цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и символа пробела _. Эти цифры записывают по одной в ячейке (подряд, без пропусков).

Оказывается достаточным иметь два внутренних состояния машины: q1 и q2.

Предположим, что в начальный момент головка находится над одной из цифр числа, а машина находится в состоянии q1. Тогда задача может быть решена в два этапа: движения головки к цифре единиц числа (во внутреннем состоянии q1) и замене этой цифры на единицу большую (с учетом переноса 1 в следующий разряд, если это 9, во внутреннем состоянии q2). Соответствующая схема МТ может иметь вид:

ai	qi
q1	q2
	0 П q1	1 С q2
	1 П q1	2 С q2
	2 П q1	3 С q2
	3 П q1	4 С q2
	4 П q1	5 С q2
	5 П q1	6 С q2
	6 П q1	7 С q2
	7 П q1	8 С q2
	8 П q1	9 С q2
	9 П q1	0 С q2
_	_ Л q1	1 С q2

2. Алгоритм записи числа в десятичной системе счисления.

Дана конечная последовательность меток, записанных в клетки ленты подряд, без пропусков. Требуется записать в десятичной системе число этих меток (пересчитать метки).

Суть алгоритма может состоять в том, что к числу 0, записанному на ленте в начале работы машины, машина добавляет 1, стирая метку за меткой, так что вместо нуля возникает число 0+k.

Легко могут быть построены алгоритмы сложения чисел, их перемножения, на­хождения наибольшего общего делителя и т.д. Однако, главная цель введения машин Поста и Тьюринга не программирование для них, а изучение свойств алгоритмов и проблемы алгоритмической разрешимости задач.

Нормальные алгоритмы Маркова. Для формализации понятия алгоритма российский математик А.А.Марков предложил использовать ассоциативные исчисления.

Рассмотрим некоторые понятия ассоциативного исчисления. Пусть имеется ал­фавит (конечный набор различных символов). Составляющие его символы будем называть буквами. Любая конечная последовательность букв алфавита (линейный их ряд) называется словом в этом алфавите.

Рассмотрим два слова N и М в некотором алфавите А. Если N является частью М, то говорят, что N входит в М.

Зададим в некотором алфавите конечную систему подстановок N-М, S-Т,..., где N, М, S, Т,... – слова в этом алфавите. Любую подстановку N-М можно приме­нить к некоторому слову К следующим способом: если в К имеется одно или не­сколько вхождений слова N, то любое из них может быть заменено словом М, и, наоборот, если имеется вхождение М, то его можно заменить словом N.

Например, в алфавите А = {а, b, с} имеются слова N=ab, М=bcb, К=аbсbсbаb. Заменив в слове К слово N на М, получим bcbcbcbab или abcbcbbcb, и, наоборот, заменив М на N, получим aabcbab или abcabab.

Подстановка ab-bcb недопустима к слову bacb, так как ни ab, ни bcb не входит в это слово. К полученным с помощью допустимых подстановок словам можно снова применить допустимые подстановки и т.д. Совокупность всех слов в данном алфавите вместе с системой допустимых подстановок называют ассоциа­тивным исчислением. Чтобы задать ассоциативное исчисление, достаточно задать алфавит и систему подстановок.

Слова P1 и P2 в некотором ассоциативном исчислении называются смежными, если одно из них может быть преобразовано в другое однократным применением допустимой подстановки.

Последовательность слов Р, P1, Р2,..., М называется дедуктивной цепочкой, веду­щей от слова Р к слову М, если каждое из двух рядом стоящих слов этой цепочки – смежное.

Слова Р и М называют эквивалентными, если существует цепочка от Р к М и обратно.

Пример:

Алфавит Подстановки

{а, b,с,d, е} ас – са; abac – abace;

ad – da; eca – ae;

bc – cb; eda – be;

bd – db; edb – be.

Слова abcde и acbde – смежные (подстановка bc – cb). Слова abcde – cadbe эквива­лентны.

abcde ® acbde ® cabde ® cadbe

(bc-cb) (ac-ca) (bd-db)

Может быть рассмотрен специальный вид ассоциативного исчисления, в кото­ром подстановки являются ориентированными: N®М (стрелка означает, что подстановку разрешается производить лишь слева направо). Для каждого ассоциа­тивного исчисления существует задача: для любых двух слов определить, являются ли они эквивалентными или нет.

Любой процесс вывода формул, математические выкладки и преобразования так­же являются дедуктивными цепочками в некотором ассоциативном исчислении. Построение ассоциативных исчислений является универсальным методом детермини­рованной переработки информации и позволяет формализовать понятие алгоритма.

Введем понятие алгоритма на основе ассоциативного исчисления: алгоритмом в алфавите А называется понятное точное предписание, определяющее процесс над словами из А и допускающее любое слово в качестве исходного. Алгоритм в алфавите А задается в виде системы допустимых подстановок, дополненной точным предписанием о том, в каком порядке нужно применять допустимые подстановки и когда наступает остановка.

Пример:

Алфавит: Система подстановок В:

А = {а, b, с} cb-cc

сса – ab

ab – bса

Предписание о применении подстановок: в произвольном слове Р надо сделать возможные подстановки, заменив левую часть подстановок на правую; повторить процесс с вновь полученным словом.

Так, применяя систему подстановок В из рассмотренного примера к словам babaac и bcacabc, получаем:

b ab aac ® bbcaaac ® остановка, т.к. в полученном слове больше нет допустимых подстановок;

bcac ab c ® bca cb cac ® bcac cca c ® bcacabc ® бесконечный процесс (остановки нет), так как мы получили исходное слово.

Предложенный А.А.Марковым способ уточнения понятия алгоритма основан на понятии нормального алгоритма, который определяется следующим образом. Пусть задан алфавит А и система подстановок В. Для произвольного слова Р подстановки из В подбираются в том же порядке, в каком они следуют в В. Если подходящей подстановки нет, то процесс останавливается. В противном случае берется первая из подходящих подстановок и производится замена ее правой частью первого вхождения ее левой части в Р. Затем все действия повторяются для получившегося слова P1. Если применяется последняя подстановка из системы В, процесс останавливается.

Такой набор предписаний вместе с алфавитом А и набором подстановок В опре­деляют нормальный алгоритм. Процесс останавливается только в двух случаях: 1) когда подходящая подстановка не найдена; 2) когда применена последняя под­становка из их набора. Различные нормальные алгоритмы отличаются друг от друга алфавитами и системами подстановок.

Приведем пример нормального алгоритма, описывающего сложение натураль­ных чисел (представленных наборами единиц).

Пример:

Алфавит: Система подстановок В:

А= {+, 1} 1 + ® + 1

+ 1 ® 1

1 ® 1

Слово Р: 11+11+111.

Последовательная переработка слова Р с помощью нормального алгоритма Маркова проходит через следующие этапы:

Р = 1 1+ 11+111 Р5 = + 1+ 111111

Р1 = 1+ 111+111 Р6 = + +1 111111

Р2 = +111 1+ 111 Р7 = +1 111111

Р3 = +11 1+ 1111 Р8 = 1111111

Р4 = +1 1+ 11111 Р9 = 1111111

С Р по Р5 переработка осуществляется с помощью первой подстановки. В Р6, Р7 используется вторая подстановка, т.к. первые подстановки исчерпаны. В Р8, Р9 применяется последняя подстановка и процесс останавливается.

Нормальный алгоритм Маркова можно рассматривать как универсальную форму задания любого алгоритма. Универсальность нормальных алгоритмов декларируется принципом нормализации: для любого алгоритма в произвольном конечном алфави­те A можно построить эквивалентный ему нормальный алгоритм над алфавитом А.

Разъясним последнее утверждение. В некоторых случаях не удается построить нормальный алгоритм, эквивалентный данному в алфавите А, если использовать в подстановках алгоритма только буквы этого алфавита. Однако, можно построить требуемый нормальный алгоритм, производя расширение алфавита А (добавляя к нему некоторое число новых букв). В этом случае говорят, что построенный алго­ритм является алгоритмом над алфавитом А, хотя он будет применяться лишь к словам в исходном алфавите А.

Если алгоритм N задан в некотором расширении алфавита А, то говорят, что N есть нормальный алгоритм над алфавитом A.

Условимся называть тот или иной алгоритм нормализуемым, если можно по­строить эквивалентный ему нормальный алгоритм, и ненормализуемым в против­ном случае. Принцип нормализации теперь может быть высказан в видоизмененной форме: все алгоритмы нормализуемы.

Данный принцип не может быть строго доказан, поскольку понятие произволь­ного алгоритма не является строго определенным и основывается на том, что все известные в настоящее время алгоритмы являются нормализуемыми, а способы композиции алгоритмов, позволяющие строить новые алгоритмы из уже известных, не выходят за пределы класса нормализуемых алгоритмов. Ниже перечислены способы композиции нормальных алгоритмов.

· Суперпозиция алгоритмов. При суперпозиции двух алгоритмов А и В выходное слово первого алгоритма рассматривается как входное слово второго алгоритма В; результат суперпозиции С может быть представлен в виде С(р) = В(А(р)).

· Объединение алгоритмов. Объединением алгоритмов А и В в одном и том же алфавите называется алгоритм С в том же алфавите, преобразующий любое слово р, содержащееся в пересечении областей определения алгоритмов А и В, в записан­ные рядом слова А(р) и В(р).

· Разветвление алгоритмов. Разветвление алгоритмов представляет собой ком­позицию D трех алгоритмов А, В и С, причем область определения алгоритма D является пересечением областей определения всех трех алгоритмов А, В и С, а для любого слова, р из этого пересечения D(p) = А(р), если С(р) = е, D(p) = B(p), если С(р) = е, где е – пустая строка.

· Итерация алгоритмов. Итерация (повторение) представляет собой такую композицию С двух алгоритмов А и В, что для любого входного слова р соответст­вующее слово С(р) получается в результате последовательного многократного применения алгоритма А до тех пор, пока не получится слово, преобразуемое алгоритмом В.

Нормальные алгоритмы Маркова являются не только средством теоретических построений, но и основой специализированного языка программирования, приме­няемого как язык символьных преобразований при разработке систем искусствен­ного интеллекта. Это один из немногих языков, разработанных в России и полу­чивших известность во всем мире.

Существует строгое доказательство того, что по возможностям преобразования нормальные алгоритмы Маркова эквивалентны машинам Тьюринга.