
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическая мера информацииСодержание книги
Поиск на нашем сайте
В статистической теории информации вводится более общая мера количества информации, в соответствии с которой рассматривается не само событие, а информация о нем. Этот вопрос глубоко проработан К. Шенноном в работе “Избранные труды по теории информации”. Если появляется сообщение о часто встречающемся событии, вероятность появления которого близка к единице, то такое сообщение для получателя малоинформативно. Столь же малоинформативны сообщения о событиях, вероятность появления которых близка к нулю. События можно рассматривать как возможные исходы некоторого опыта, причем все исходы этого опыта составляют полную группу событий. К. Шеннон ввел понятие неопределенности ситуации, возникающей в процессе опыта, назвав ее энтропией. Энтропия полной группы событий есть количественная мера ее неопределенности и, следовательно, информативности, количественно выражаемая как средняя функция множества вероятностей каждого из возможных исходов опыта. Иными словами, количество информации, получаемое в результате проведения опыта, равно снятой во время этого опыта неопределенности. Для понимания вероятностного подхода лучше всего рассмотреть несложный пример, связанный с бросанием правильной игральной кости, имеющей N граней (наиболее распространенным является случай шестигранной кости: N = 6). Результатом данного опыта может быть выпадение грани с одним из следующих знаков: 1, 2,... N. Введем в рассмотрение численную величину, измеряющую неопределенность -энтропию (обозначим ее Н). Величины N и Н связаны между собой некоторой функциональной зависимостью:
а сама функция f является возрастающей, неотрицательной и определенной (в рассматриваемом нами примере) для N = 1, 2,... 6. Рассмотрим процедуру бросания кости более подробно: 1) готовимся бросить кость; исход опыта неизвестен, т.е. имеется некоторая неопределенность; обозначим ее Н1; 2) кость брошена; информация об исходе данного опыта получена; обозначим количество этой информации через I; 3) обозначим неопределенность данного опыта после его осуществления через H2. За количество информации, которое получено в ходе осуществления опыта, примем разность неопределенностей “до” и “после” опыта:
Очевидно, что в случае, когда получен конкретный результат, имевшаяся неопределенность снята (H2=0), и, таким образом, количество полученной информации совпадает с первоначальной энтропией. Иначе говоря, неопределенность, заключенная в опыте, совпадает с информацией об исходе этого опыта. Заметим, что значение H2 могло быть и не равным нулю, например, в случае, когда в ходе опыта следующей выпала грань со значением, большим трех. Следующим важным моментом является определение вида функции f в формуле (2.3). Если варьировать число граней N и число бросаний кости (обозначим эту величину через М), общее число исходов (векторов длины М, состоящих из знаков 1, 2,..., N) будет равно N в степени М:
Так, в случае двух бросаний кости с шестью гранями имеем: Х=62=36. Фактически каждый исход Х есть некоторая пара (X1, X2), где Х1 и X2 – соответственно исходы первого и второго бросаний (общее число таких пар – X). Ситуацию с бросанием М раз кости можно рассматривать как некую сложную систему, состоящую из независимых друг от друга подсистем – “однократных бросаний кости”. Энтропия такой системы в М раз больше, чем энтропия одной системы (так называемый “принцип аддитивности энтропии”):
Из приведенных формул выводится мера Хартли:
Важным при введении какой-либо величины является вопрос о том, что принимать за единицу ее измерения. Очевидно, H будет равно единице при N = 2. Иначе говоря, в качестве единицы измерения информации принимается количество информации, связанное с проведением опыта, состоящего в получении одного из двух равновероятных исходов (примером такого опыта может служить бросание монеты при котором возможны два исхода: “орел”, “решка”). Такая единица количества информации называется бит. В случае, когда вероятности различных исходов опыта не равновероятны (а имеют вероятности Pi), меру энтропии вычисляют по формуле Шеннона:
В качестве примера определим количество информации, связанное с появлением каждого символа в сообщениях, записанных на русском языке. Будем считать, что русский алфавит состоит из 33 букв и знака “пробел” для разделения слов. По формуле (2.7) получаем: Н» 5 бит. Однако, в словах русского языка (равно как и в словах других языков) различные буквы встречаются неодинаково часто. Для учета данного обстоятельства воспользуемся для подсчета Н вероятностными частотами употребления различных знаков русского алфавита, полученных на основе анализа очень больших по объему текстов. По формуле (2.8) получаем: Н» 4.72 бит. Полученное значение Н, как и можно было предположить, меньше вычисленного ранее. Величина Н, вычисляемая по формуле (2.7), является максимальным количеством информации, которое могло бы приходиться на один знак.
|
||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 179; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.85.96 (0.005 с.) |

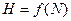 , (2.3)
, (2.3) (2.4)
(2.4) (2.5)
(2.5)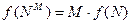 (2.6)
(2.6) (2.7)
(2.7) (2.8)
(2.8)


