
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретические основы информатикиСодержание книги
Поиск на нашем сайте
ИНФОРМАТИКА ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНФОРМАТИКИ Разработано Воробьевым А.В., Воробьевой Т.В. Рецензент Костин Г.А., канд. техн. наук Ведущий рецензент Суханов А.А., канд. техн. наук
Рекомендовано Министерством образования Российской Федерации в качестве учебного пособия для студентов высших учебных заведений
КУРС: ИНФОРМАТИКА
В данном учебном пособии вводится понятие информатики и рассматриваются некоторые теоретические аспекты информатики: информация и ее измерение, представление чисел в различных системах счисления, устройства обработки информации, теория алгоритмов и абстрактные автоматы. Кроме того, описываются этапы информационного процесса в автоматизированных системах.
ОГЛАВЛЕНИЕ
ДИДАКТИЧЕСКИЙ ПЛАН.. 2 ЛИТЕРАТУРА.. 2 ПЕРЕЧЕНЬ УМЕНИЙ.. 2 ТЕМАТИЧЕСКИЙ ОБЗОР. 3 1. ИНФОРМАТИКА КАК НАУКА И КАК ВИД ПРАКТИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ.. 3 1.1. Основные понятия информатики. Информационный ресурс. 3 1.1.1. Объект и предмет информатики. 3 1.1.2. Структура современной информатики. 4 1.1.3. Информационные ресурсы.. 5 1.2. История развития информатики. 5 1.3. Место информатики в ряду других фундаментальных наук. 6 1.4. Информационные технологии. 6 1.5. Социально-экономические аспекты информационных технологий. 7 1.6. Правовые и этические аспекты информационных технологий. 8 2. ИНФОРМАЦИЯ.. 9 2.1. Понятие информации. Носители информации. Сигналы.. 9 2.2. Измерение информации. Энтропия. Количество информации. 10 2.2.1. Структурная мера информации. 10 2.2.2. Статистическая мера информации. 11 2.2.3. Семантическая мера информации. 12 2.3. Свойства информации. 12 3. ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ ОБРАБОТКИ ИНФОРМАЦИИ.. 13 3.1. Абстрактные автоматы и понятие алгоритма. Программное управление. 13 3.1.1. Понятие алгоритма. 13 3.1.2. Формализация алгоритма. Абстрактные автоматы.. 14 3.2. Обработка аналоговой и цифровой информации. Кодирование информации. 19 3.3. Системы счисления. Методы перевода чисел из одной системы счисления в другую.. 21 3.3.1. Основные понятия. 21 3.3.2. Двоичная система счисления. 22 3.3.3. Восьмеричная и шестнадцатеричная системы счисления. 23 3.4. Устройства обработки информации и их характеристики. 24 3.4.1. Краткая история развития устройств обработки информации. 24 3.4.2. Классическая архитектура ЭВМ... 25 3.4.3. Характеристика основных блоков ЭВМ... 26 3.4.4. Основной цикл работы ЭВМ... 28 3.4.5. Накопители информации. 29 3.4.6. Внешние устройства ЭВМ... 30 4. АВТОМАТИЗИРОВАННЫЕ ИНФОРМАЦИОННЫЕ СИСТЕМЫ (АИС) 32 4.1. Классификация АИС.. 32 4.2. Информационный процесс в автоматизированных системах. Фазы информационного цикла и их модели. 35 4.2.1. Этапы информационного процесса в АИС.. 35 4.2.2. Сбор и преобразование информации. 37 4.2.3. Передача информации. 37 4.2.4. Обработка информации. 38 ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ... 39 ТРЕНИНГ УМЕНИЙ.. 41 ГЛОССАРИЙ.. 46 ДИДАКТИЧЕСКИЙ ПЛАН Основные понятия информатики. Информационный ресурс. История развития информатики. Место информатики в ряду других фундаментальных наук. Информационные технологии. Социально-экономические аспекты информационных технологий. Правовые и этические аспекты информационных технологий. Понятие информации. Носители информации. Сигналы. Измерение информации. Количество информации. Энтропия. Свойства информации. Абстрактные автоматы и понятие алгоритма. Программное управление (теория алгоритмов, формализация). Обработка аналоговой и цифровой информации. Кодирование информации. Системы счисления. Методы перевода чисел из одной системы счисления в другую. Устройства обработки данных и их характеристики. Классификация АИС. Информационный процесс в автоматизированных системах. Фазы информационного цикла и их модели. ЛИТЕРАТУРА
Базовая 1. Информатика. Под ред. Н.В.Макаровой. – М., 2000.
Дополнительная 2. А.В.Могилев, Н.И.Пак, Е.К.Хеннер. Информатика. – М., 2000. 3. Информатика. Базовый курс. Под ред.Симоновича.– С-Пб., 2001. 4. В.А.Острейковский. Информатика. – М., 2001. 5. А.Я.Савельев. Основы информатики. – М., 2001. 6. И.П.Норенков, В.А.Трудоношин. Телекоммуникационные технологии и сети. – М., 2000. 7. В.Н.Петров. Информационные системы. – С-Пб., 2002.
ПЕРЕЧЕНЬ УМЕНИЙ
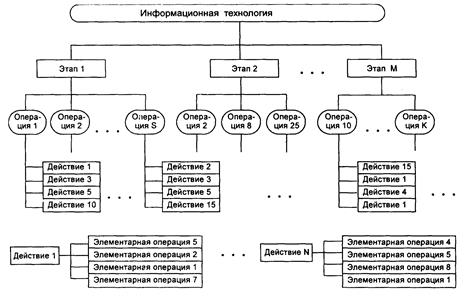
ТЕМАТИЧЕСКИЙ ОБЗОР (Жирным шрифтом выделены новые понятия, которые необходимо усвоить. Знание этих понятий будет проверяться при тестировании). ИНФОРМАТИКА КАК НАУКА И КАК ВИД ПРАКТИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ Основные понятия информатики. Информационный ресурс Информационные ресурсы Ресурс – запасы, источники чего-нибудь. Такая трактовка приведена в “Словаре русского языка” С.И. Ожегова. В индустриальном обществе, где большая часть усилий направлена на материальное производство, известно несколько основных видов ресурсов, ставших уже классическими экономическими категориями: · материальные ресурсы – совокупность предметов труда, предназначенных для использования в процессе производства общественного продукта, например сырье, материалы, топливо, энергия, полуфабрикаты, детали и т.д.; · природные ресурсы – объекты, процессы, условия природы, используемые обществом для удовлетворения материальных и духовных потребностей людей; · трудовые ресурсы – люди, обладающие общеобразовательными и профессиональными знаниями для работы в обществе; · финансовые ресурсы – денежные средства, находящиеся в распоряжении государственной или коммерческой структуры; · энергетические ресурсы – носители энергии, например уголь, нефть, нефтепродукты, газ, гидроэнергия, электроэнергия и т.д. Одним из ключевых понятий при информатизации общества стало понятие «информационные ресурсы», толкование и обсуждение которого велось с того момента, когда начали говорить о переходе к информационному обществу. Этому вопросу посвящено довольно много публикаций, в которых отразились и разные мнения и определения, и разные научные школы, рассматривающие эти понятия. Информационные ресурсы – отдельные документы и отдельные массивы документов, документы и массивы документов в информационных системах (библиотеках, архивах, фондах, банках данных, других информационных системах). Надо понимать, что документы и массивы информации не существуют сами по себе. В них в разных формах представлены знания, которыми обладали люди, создававшие их. Таким образом, информационные ресурсы – это знания, подготовленные людьми для социального использования в обществе и зафиксированные на материальном носителе. Информационные ресурсы общества, если их понимать как знания, отчуждены от тех людей, которые их накапливали, обобщали, анализировали, создавали и т.п. Эти знания материализовались в виде документов, баз данных, баз знаний, алгоритмов, компьютерных программ, а также произведений искусства, литературы, науки. В настоящее время не разработана методология количественной и качественной оценки информационных ресурсов, а также прогнозирования потребностей общества в них. Это снижает эффективность информации, накапливаемой в виде информационных ресурсов, и увеличивает продолжительность переходного периода от индустриального общества к информационному. Кроме того, неизвестно, какой объем трудовых ресурсов должен быть задействован в сфере производства и распространения информационных ресурсов в информационном обществе. Несомненно, в будущем эти проблемы будут решены. Информационные ресурсы страны, региона, организации должны рассматриваться как стратегические ресурсы, аналогичные по значимости запасам сырья, энергии, ископаемых и прочим ресурсам. Рис. 1.2. К вопросу о месте информатики в системе наук Однако многие ученые подчеркивают, что информатика имеет характерные черты и других групп наук – технических и гуманитарных (или общественных). Черты технической науки придают информатике ее аспекты, связанные с созданием и функционированием машинных систем обработки информации. Так, академик А.А.Дородницын определяет состав информатики как “три неразрывно и существенно связанные части: технические средства, программные и алгоритмические”. Науке информатике присущи и некоторые черты гуманитарной (общественной) науки, что обусловлено ее вкладом в развитие и совершенствование социальной сферы. Таким образом, информатика является комплексной, междисциплинарной отраслью научного знания, как это изображено на рис. 1.2. Информационные технологии Информационная технология – процесс, использующий совокупность средств и методов сбора, обработки и передачи данных (первичной информации) для получения информации нового качества о состоянии объекта, процесса или явления (информационного продукта). Цель информационной технологии – производство информации для ее анализа человеком и принятия на его основе решения по выполнению какого-либо действия. Информационная технология является наиболее важной составляющей процесса использования информационных ресурсов общества. К настоящему времени она прошла несколько эволюционных этапов, смена которых определялась главным образом развитием научно-технического прогресса, появлением новых технических средств переработки информации. В современном обществе основным техническим средством технологии переработки информации служит персональный компьютер, который существенно повлиял как на концепцию построения и использования технологических процессов, так и на качество результатной информации. Внедрение персонального компьютера в информационную сферу и применение телекоммуникационных средств связи определили новый этап развития информационной технологии и, как следствие, изменение ее названия за счет присоединения одного из синонимов: «новая», «компьютерная» или «современная». Инструментарий информационной технологии – один или несколько взаимосвязанных программных продуктов для определенного типа компьютера, технология работы в котором позволяет достичь поставленную пользователем цель. В качестве инструментария можно использовать следующие распространенные виды программных продуктов для персонального компьютера: текстовый процессор (редактор), настольные издательские системы, электронные таблицы, системы управления базами данных, электронные записные книжки, электронные календари, информационные системы функционального назначения (финансовые, бухгалтерские, для маркетинга и пр.), экспертные системы и т.д. Информационная технология является процессом, состоящим из четко регламентированных правил выполнения операций, действий, этапов разной степени сложности над данными, хранящимися в компьютерах. Основная цель информационной технологии – в результате целенаправленных действий по переработке первичной информации получить необходимую для пользователя информацию. Информационная технология тесно связана с информационными системами, которые являются для нее основной средой. Информационная система является средой, составляющими элементами которой являются компьютеры, компьютерные сети, программные продукты, базы данных, люди, различного рода технические и программные средства связи и т.д. Основная цель информационной системы – организация хранения и передачи информации. Информационная система представляет собой человеко-компьютерную систему обработки информации. На рис. 1.3 технологический процесс переработки информации представлен в виде иерархической структуры по уровням.
Рис.1.3. Представление информационной технологии в виде иерархической структуры, состоящей из этапов, действий, операций Необходимо понимать, что освоение информационной технологии и дальнейшее ее использование должны свестись к тому, что вы должны сначала хорошо овладеть набором элементарных операций, число которых ограничено. Из этого ограниченного числа элементарных операций в разных комбинациях составляется действие, а из действий, также в разных комбинациях, составляются операции, которые определяют тот или иной технологический этап. Совокупность технологических этапов образует технологический процесс (технологию). Информационная технология, как и любая другая, должна отвечать следующим требованиям: · обеспечивать высокую степень расчленения всего процесса обработки информации на этапы (фазы), операции, действия; · включать весь набор элементов, необходимых для достижения поставленной цели; · иметь регулярный характер. Этапы, действия, операции технологического процесса могут быть стандартизированы и унифицированы, что позволит более эффективно осуществлять целенаправленное управление информационными процессами. ИНФОРМАЦИЯ Структурная мера информации Информация всегда представляется в виде сообщения. Элементарная единица сообщений – символ. Символы, собранные в группы, – слова. Сообщение, оформленное в виде слов или отдельных символов, всегда передается в материально-энергетической форме (электрический, световой, звуковой сигналы и т. д.). Различают информацию непрерывную и дискретную.
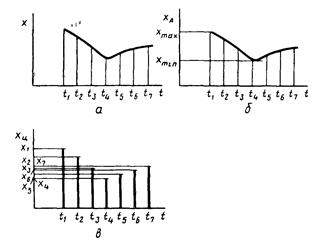
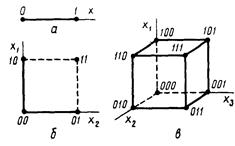
Функция x(t), изображенная на рис. 2.1, а, может быть представлена в непрерывном (рис. 2.1, б) и дискретном (рис. 2.1, в) видах. В непрерывном виде эта функция может принимать любые вещественные значения в данном диапазоне изменения аргумента t, т. е. множество значений непрерывной функции бесконечно. В дискретном виде функция x(t) может принимать вещественные значения только при определенных значениях аргумента. Какой бы малый интервал дискретности (т. е. расстояние между соседними значениями аргумента) ни выбирался, множество значений дискретной функции для заданного диапазона изменений аргумента (если он не бесконечный) будет конечно (ограничено). При использовании структурных мер информации учитывается только дискретное строение сообщения, количество содержащихся в нем информационных элементов, связей между ними. При структурном подходе различаются геометрическая, комбинаторная и аддитивная меры информации. Геометрическая мера предполагает измерение параметра геометрической модели информационного сообщения (длины, площади, объема и т. п.) в дискретных единицах. Например, геометрической моделью информации может быть линия единичной длины (рис 2.2,а – одноразрядное слово, принимающее значение 0 или 1), квадрат (рис. 2.2,б– двухразрядное слово) или куб (рис 2.2,в – трехразрядное слово). Максимально возможное количество информации в заданных структурах определяет информационную емкость модели (системы), которая определяется как сумма дискретных значений по всем измерениям (координатам). В комбинаторной мере количество информации определяется как число комбинаций элементов (символов). Возможное количество информации совпадает с числом возможных сочетаний, перестановок и размещений элементов. Комбинирование символов в словах, состоящих только из 0 и 1, меняет значения слов. Рассмотрим две пары слов 100110 и 001101, 011101 и 111010. В них проведена перестановка крайних разрядов (изменено местоположение знакового разряда в числе – перенесен слева направо). Аддитивная мера (мера Хартли), в соответствии с которой количество информации измеряется в двоичных единицах (битах), наиболее распространена. Вводятся понятия глубины q и длины n числа. Глубина числа q – количество символов (элементов), принятых для представления информации. В каждый момент времени реализуется только один какой-либо символ. Глубина числа соответствует основанию системы счисления. Длина числа n – количество позиций, необходимых и достаточных для представления чисел заданной величины. Длина числа соответствует разрядности системы счисления.
При заданных глубине и длине числа количество чисел, которое можно представить, N = qn. Величина N неудобна для оценки информационной емкости. Хартли ввел аддитивную двоичную логарифмическую меру, позволяющую вычислять количество информации в двоичных единицах – битах: I = log2N = n log2 q (2.1) При n = 1, q = 2 I = log2 2 = 1 бит. Это и есть единица информации по Хартли. Следовательно, 1 бит информации соответствует одному элементарному событию, которое может произойти или не произойти. Такая мера количества информации удобна тем, что она обеспечивает возможность оперировать мерой как числом. Количество информации при этом эквивалентно количеству двоичных символов 0 или 1. При наличии нескольких источников информации общее количество информации:
где I(qk) – количество информации от источника k. Логарифмическая мера информации позволяет измерять количество информации и используется на практике. Свойства информации Информация является динамическим объектом, образующимся в момент взаимодействия объективных данных и субъективных методов. Как и всякий объект, она обладает свойствами (объекты различимы по своим свойствам). Характерной особенностью информации, отличающей ее от других объектов природы и общества, является отмеченный выше дуализм: на свойства информации влияют как свойства данных, составляющих ее содержательную часть, так и свойства методов, взаимодействующих с данными в ходе информационного процесса. По окончании информационного процесса свойства информации переносятся на свойства новых данных, то есть свойства методов могут переходить на свойства данных. Можно привести немало разнообразных свойств информации. Каждая научная дисциплина рассматривает те свойства информации, которые ей наиболее важны. Рассмотрим наиболее важные свойства информации с позиций изучаемой дисциплины. Объективность и субъективность информации. Понятие объективности информации является относительным. Это понятно, если учесть, что методы являются субъективными. Более объективной принято считать ту информацию, в которую методы вносят меньший субъективный элемент. Так, например, принято считать, что в результате наблюдения фотоснимка природного объекта или явления образуется более объективная информация, чем в результате наблюдения рисунка того же объекта, выполненного человеком. В ходе информационного процесса степень объективности информации всегда понижается. Это свойство учитывают, например, в правовых дисциплинах, где по-разному обрабатываются показания лиц, непосредственно наблюдавших события или получивших информацию косвенным путем (посредством умозаключений или со слов третьих лиц). В не меньшей степени объективность информации учитывают в исторических дисциплинах. Одни и те же события, зафиксированные в исторических документах разных стран и народов, выглядят совершенно по-разному. У историков имеются свои методы для тестирования объективности исторических данных и создания новых, более достоверных данных путем сопоставления, фильтрации и селекции исходных данных. Обратим внимание на то, что здесь речь идет не о повышении объективности данных, а о повышении их достоверности (это совсем другое свойство). Полнота информации во многом характеризует качество информации и определяет достаточность данных для принятия решений или для создания новых данных на основе имеющихся. Чем полнее данные, тем шире диапазон методов, которые можно использовать, тем проще подобрать метод, вносящий минимум погрешностей в ход информационного процесса. Адекватность информации – это степень соответствия информации, полученной в информационном процессе, реальному объективному состоянию дела. Неадекватная информация может образовываться при создании новой информации на основе неполных или недостоверных данных. Однако и полные, и достоверные данные могут приводить к созданию неадекватной информации в случае применения к ним неадекватных методов. Доступность информации – мера возможности получить ту или иную информацию. На степень доступности информации влияют одновременно как доступность данных, так и доступность адекватных методов для их интерпретации. Отсутствие доступа к данным при наличии адекватных методов обработки данных приводят к одинаковому результату: информация оказывается недоступной. Отсутствие адекватных методов для работы с данными во многих случаях приводит к применению неадекватных методов, в результате чего образуется неполная, неадекватная или недостоверная информация. Актуальность информации – это степень соответствия информации текущему моменту времени. Нередко с актуальностью, как и с полнотой, связывают коммерческую ценность информации. Поскольку информационные процессы растянуты во времени, то достоверная и адекватная, но устаревшая информация может приводить к ошибочным решениям. Необходимость поиска (или разработки) адекватного метода для работы с данными может приводить к такой задержке в получении информации, что она становится неактуальной и ненужной. На этом, в частности, основаны многие современные системы шифрования данных с открытым ключом. Лица, не владеющие ключом (методом) для чтения данных, могут заняться поиском ключа, поскольку алгоритм его работы доступен, но продолжительность этого поиска столь велика, что за время работы информация теряет актуальность и, соответственно, связанную с ней практическую ценность. Точность информации определяется степенью близости получаемой информации к реальному состоянию объекта, процесса, явления и т.п. Для информации, отображаемой цифровым кодом, известны четыре классификационных понятия точности: · формальная точность, измеряемая значением единицы младшего разряда числа; · реальная точность, определяемая значением единицы последнего разряда числа, верность которого гарантируется; · максимальная точность, которую можно получить в конкретных условиях функционирования системы; · необходимая точность, определяемая функциональным назначением показателя. Достоверность информации определяется ее свойством отражать реально существующие объекты с необходимой точностью. Измеряется достоверность информации доверительной вероятностью необходимой точности, т.е. вероятностью того, что отображаемое информацией значение параметра отличается от истинного значения этого параметра в пределах необходимой точности. Устойчивость информации отражает ее способность реагировать на изменения исходных данных без нарушения необходимой точности. Устойчивость информации, как и репрезентативность, обусловлена выбранной методикой ее отбора и формирования. Своевременность информации означает ее поступление не позже заранее назначенного момента времени, согласованного со временем решения поставленной задачи. Понятие алгоритма Существует много определений термина “алгоритм”. Например, по определению академика А. Н. Колмогорова, алгоритм или алгорифм – это всякая система вычислений, выполняемых по строго определенным правилам, которая после какого-либо числа шагов заведомо приводит к решению поставленной задачи. В инженерной практике часто используется следующее определение: алгоритм – конечная совокупность точно сформулированных правил решения какой-то задачи. Само слово “алгоритм” происходит от algorithmi – латинской формы написания имени великого математика IX века аль-Хорезми, который сформулировал правила выполнения арифметических действий. Первоначально под алгоритмами и понимали только правила выполнения четырех арифметических действий над многозначными числами. По форме задания алгоритмы могут быть словесными и математическими. Пример словесной формы алгоритма – алгоритм Евклида для нахождения наибольшего общего делителя двух чисел а и b приводится ниже. 1. Обозревая два числа а и b, переходи к следующему пункту. 2. Сравни обозреваемые числа (а равно b, а меньше, больше b) и переходи к следующему пункту. 3. Если а и b равны, то прекрати вычисление: каждое из чисел дает искомый результат. Если числа не равны, то переходи к следующему пункту. 4. Если первое число меньше второго, то переставь их местами и переходи к следующему пункту. 5. Вычти второе число из первого и сделай обозрение двух чисел: вычитаемого и остатка; переходи к п. 2. По указаниям этого алгоритма можно найти наибольший общий делитель для любой пары целых чисел. Характеристиками алгоритма являются: · детерминированность, определяющая однозначность результата решения задачи при заданных исходных данных; · дискретность определяемого алгоритмом процесса, означающая расчлененность его на отдельные элементарные шаги; · массовость, позволяющая применять один и тот же алгоритм для некоторого множества однотипных задач. Эти характеристики не дают точного описания алгоритма, а лишь объясняют смысл этого термина в математике. Пример алгебраической формы алгоритма – любая математическая формула для нахождения какой-то величины. Однако для того, чтобы реализовать математическую форму алгоритма, требуется дать еще ряд словесных указаний, показать область применения алгоритма. Детерминированный алгоритм – алгоритм, имеющий место при четкой и ясной системе правил и указаний и однозначных действиях. Случайный алгоритм – алгоритм, предусматривающий возможность случайного выбора тех или иных правил. Алгоритм должен обеспечивать получение результата через конечное число шагов для любой задачи определенного класса. В противном случае задача неразрешима. Нахождение алгоритма решения задачи называется алгоритмизацией. Процесс выполнения алгоритма называется алгоритмическим процессом. Для некоторых исходных данных он заканчивается получением искомого результата после конечного числа шагов. Однако возможны случаи, когда искомый результат не достигается или безрезультатно обрывается. Тогда говорят, что к таким исходным данным алгоритм неприменим. Таким образом, алгоритм дает возможность ответить на вопрос “что делать?” в каждый момент времени, однако создать алгоритм не всегда возможно. Численный алгоритм – алгоритм, соответствующий решению поставленной задачи с помощью арифметических действий. Логический алгоритм – алгоритм, используемый в случае, если при решении задачи приходится применять некоторые логические действия. Процесс решения задачи на ЭВМ прежде всего должен быть выражен каким-то алгоритмом. Разработка алгоритмов решения задач – задача программиста, а разработка алгоритмов функционирования цифрового автомата для решения поставленных задач – задача инженера-разработчика. Основные понятия Система счисления – совокупность приемов и правил для записи чисел цифровыми знаками или символами. Все системы счисления можно разделить на два класса: позиционные и непозиционные. В классе позиционных систем для записи чисел в различных системах счисления используется некоторое количество отличных друг от друга знаков. Число таких знаков в позиционной системе счисления называется основанием системы счисления. Ниже приведена табл. 3.1, содержащая наименования некоторых позиционных систем счисления и перечень знаков (цифр), из которых образуются в них числа. Таблица 3.1 Некоторые системы счисления
В позиционной системе счисления относительной позиции цифры в числе ставится в соответствие весовой множитель, и число может быть представлено в виде суммы произведений коэффициентов на соответствующую степень основания системы счисления (весовой множитель): AnAn-1An-2...A1A0, A-1A-2...= Аn · Вn + Аn-1 · Вn-1 +…+ А1 · В1 + А0 · В0 + А-1 · В-1+ + А-2 · В-2 +… (знак “,” отделяет целую часть числа от дробной. Таким образом, значение каждого знака в числе зависит от позиции, которую занимает знак в записи числа. Именно поэтому такие системы счисления называют позиционными). Позиционная система счисления – система, в которой величина числа определяется значениями входящих в него цифр и их относительным положением в числе. Примеры (десятичный индекс внизу указывает основание системы счисления): 23,4310 = 2 · 101 + 3 · 100 + 4 · 10-1 + 3 · 10-2 (в данном примере цифра 3 в одном случае означает число единиц, а в другом – число сотых долей единицы); 69210 = 6 · 102 + 9·101 + 2. (692 с формальной точки зрения представляется в виде “шесть умножить на десять в степени два, плюс девять умножить на десять в степени один, плюс два”). 11012 = 1 · 23 + 1 · 22 + 0 · 21 + 1·20 = 1310; 1123 = 1 · 32 + 1 · 31 + 2 · 30 = 1410; 341,58 = 3 · 82 + 4 · 81 + 1 · 80 + 5 · 8-1 = 225,12510; A1F,416 = A · 162 + 1 · 161 + F · 160 + 4 · 16-1 = 2591,62510. При работе с компьютерами приходится параллельно использовать несколько позиционных систем счисления (чаще всего двоичную, десятичную, восьмеричную и шестнадцатеричную), поэтому большое практическое значение имеют процедуры перевода чисел из одной системы счисления в другую. Заметим, что во всех приведенных выше примерах результат является десятичным числом, и, таким образом, способ перевода чисел из любой позиционной системы счисления в десятичную уже продемонстрирован. В общем случае, чтобы перевести целую часть числа из десятичной системы в систему с основанием В, необходимо разделить ее на В. Остаток даст младший разряд числа. Полученное при этом частное необходимо вновь разделить на В – остаток даст следующий разряд числа и т.д. Для перевода дробной части ее необходимо умножить на В. Целая часть полученного произведения будет первым (после запятой, отделяющей целую часть от дробной) знаком. Дробную же часть произведения необходимо вновь умножить на В. Целая часть полученного числа будет следующим знаком и т.д. Конкретные примеры перевода чисел будут рассмотрены ниже. Кроме рассмотренных выше позиционных систем счисления существуют такие, в которых значение знака не зависит от того места, которое он занимает в числе. Такие системы счисления называются непозиционными. Наиболее известным примером непозиционной системы является римская. В этой системе используется 7 знаков (I, V, X, L, С, D, М), которые соответствуют следующим величинам: I(1) V(5) X(10) L(50) С (100) D(500) М(1000). Примеры: III (три), LIX (пятьдесят девять), DLV (пятьсот пятьдесят пять). Недостатком непозиционных систем, из-за которых они представляют лишь исторический интерес, является отсутствие формальных правил записи чисел и, соответственно, арифметических действий над ними (хотя по традиции римскими числами часто пользуются при нумерации глав в книгах, веков в истории и др.). Двоичная система счисления Особая значимость двоичной системы счисления в информатике определяется тем, что внутреннее представление любой информации в компьютере является двоичным, т.е. описываемым наборами только из двух знаков (0 и 1). Конкретизируем описанный выше способ в случае перевода чисел из десятичной системы в двоичную. Целая и дробная части переводятся порознь. Для перевода целой части (или просто целого) числа необходимо разделить ее на основание системы счисления и продолжать делить частные от деления до тех пор, пока частное не станет равным 0. Значения получившихся остатков, взятые в обратной последовательности, образуют искомое двоичное число. Например: Остаток 25/2=12 (1), 12/2=6 (0), 6/2=3 (0), 3/2=1 (1), 1/2=0 (1). Таким образом: 2510=110012. Для перевода дробной части (или числа, у которого “0” целых) надо умножить ее на 2. Целая часть произведения будет первой цифрой числа в двоичной системе. Затем, отбрасывая у результата целую часть, вновь умножаем на 2 и т.д. Заметим, что конечная десятичная дробь при этом вполне может стать бесконечной (периодической) двоичной. Например: 0,73·2=1,46 (целая часть 1), 0,46·2 = 0,92 (целая часть 0), 0,92·2 = 1,84 (целая часть 1), 0,84·2 = 1,68 (целая часть 1) и т.д. В итоге: 0,7310=0,10112. Над числами, записанными в л
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 213; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.195.180 (0.014 с.) |

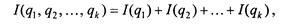 (2.2)
(2.2)


