
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы теории чисел. Функция эйлера. Теория ФермаСодержание книги
Поиск на нашем сайте
Каноническим разложением числа Функцией Эйлера называется, отображение
Например, Числа Функция Эйлера от числа Для взаимно простых Число примитивных многочленов степени Теорема Эйлера-Ферма 1). Для взаимно простых Для решения уравнения По алгоритму Евклида для получения НОД двух заданных чисел нужно одно число делить на другое, затем делить делитель на получаемый остаток до тех, пока остаток не станет равным нулю. Последний больший нуля остаток будет искомым НОД. Для чисел
где
имеет вид
Обозначим за
По определению
или
что означает
т.е. Процесс получения числителей и знаменателей удобно оформить в виде таблицы:
Таким образом, корни уравнения Пример. Решить уравнение
Затем составляется таблица для вычисления
Таким образом, искомый Гипотеза. Задача разложения целого числа с заданным числом разрядов на множители является труднорешаемой Задача называется труднорешаемой, если время ее решения зависит от объема входных данных по экспоненциальному закону и не может быть сведено к полиномиальному}. На сегодняшний день существуют весьма быстрые алгоритмы для проверки данного числа на простоту, но для разложения 200-значного числа на множители лучшим современным компьютерам по лучшим современным алгоритмам может потребоваться миллиарды лет.
Эта гипотеза лежит в основе методов Диффи-Хеллмана.
Простой и обобщенный алгоритмы Эвклида Алгори́тм Евкли́да — алгоритм для нахождения наибольшего общего делителя двух целых чисел. Алгоритм Евклида был известен в древнегреческой математике по крайней мере за век до Евклида под названием «антифайресис» — «последовательное взаимное вычитание». Евклид описал его в VII книге «Начал» для чисел и в X книге «Начал» — для величин. Алгоритм Евклида Пусть a и b суть целые числа, не равные одновременно нулю, и последовательность чисел
определена тем, что каждое rk это остаток от деления пред-предыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, т. е. a = bq 0 + r 1 b = r 1 q 1 + r 2 r 1 = r 2 q 2 + r 3
rn − 1 = rnqn Тогда (a, b), наибольший общий делитель a и b, равен rn, последнему ненулевому члену этой последовательности. Существование таких r 1, r 2,..., то есть возможность деления с остатком m на n для любого целого m и целого Корректность этого алгоритма вытекает из следующих двух утверждений: · Пусть a = bq + r, тогда (a, b) = (b, r). · (0, r) = r. для любого ненулевого r. Расширенный алгоритм Евклида и соотношение Безу Формулы для ri могут быть переписаны следующим образом: r 1 = a + b (- q 0) r 2 = b − r 1 q 1 = a (− q 1) + b (1 + q 1 q 0)
(a, b) = rn = as + bt здесь s и t целые. Это представление наибольшего общего делителя называется соотношением Безу, а числа s и t — коэффициентами Безу. Соотношение Безу является ключевым в доказательстве основной теоремы арифметики. Связь с цепными дробями · Отношение a / b допускает представление в виде цепной дроби:
· Отношение - t / s, в расширенном алгоритме Евклида допускает представление в виде цепной дроби:
Ускоренные версии алгоритма Алгоритм может быть записан в общем виде не только для целых чисел, но и для полиномов. Строго говоря, алгоритм работает в любом евклидовом кольце. Одним из методов ускорения целочисленного алгоритма Евклида является выбор симметричного остатка: · причем · Одна из наиболее многообещающих версий ускоренного алгоритма Евклида для полиномов основывается на том, что промежуточные значения алгоритма в основном зависят от высоких степеней. При применении стратегии Divide & Conqurer наблюдается большое ускорение асимптотической скорости алгоритма.
Шифр Шамира Этот шифр, предложенный Шамиром {Adi Shamir), был первым, позволяющим организовать обмен секретными сообщениями по открытой линии связи для лиц, которые не имеют никаких защищенных каналов и секретных ключей и, возможно, никогда не видели друг друга. (Напомним, что система Диффи-Хеллмана позволяет сформировать только секретное слово, а передача сообщения потребует использования некоторого шифра, где это слово будет использоваться как ключ.) Перейдем к описанию системы. Пусть есть два абонента Аи В, соединенные линией связи. А хочет передать сообщение m абоненту Б так, чтобы никто не узнал его содержание. А выбирает случайное большое простое число р и открыто передает его В. Затем А выбирает два числа сА и dA, такие, что сАdA mod (р - 1) = 1. Эти числа А держит в секрете и передавать не будет. В тоже выбирает два числа св dв, такие, что и держит их в секрете. св<dв mod (p - 1) = 1, После этого А передает свое сообщение m, используя трехступенчатый протокол. Если m < р (m рассматривается как число), то сообщение т передается сразу, если же т Описание протокола. Шаг 1. А вычисляет число Х1 =mСА modp где m — исходное сообщение, и пересылает х1 к В. Шаг 2. В, получив х1, вычисляет число X2 = х2CB mod p и передает х2 к А. Шаг 3. А вычисляет число X3 = х2dA mod p и передает его В. Шаг 4. В, получив х3, вычисляет число X4 = x3dB mod p. Шифр Эль-Гамаля Пусть имеются абоненты А, В, С,..., которые хотят передавать друг другу зашифрованные сообщения, не имея никаких защищенных каналов связи. Эль-Гамаль (Tahcr ElGamal), который решает эту задачу, используя, в отличие от шифра Шамира, только одну пересылку сообщения. Фактически здесь используется схема Диффи-Хеллмана, чтобы сформировать общий секретный ключ для двух абонентов, передающих друг другу сообщение, и затем сообщение шифруется путем умножения его на этот ключ. Для каждого следующего сообщения секретный ключ вычисляется заново. Перейдем к точному описанию метода. Для всей группы абонентов выбираются некоторое большое простое число р и число g, такие, что различные степени g суть различные числа по модулю р.Числа р и g передаются абонентам в открытом виде (они могут использоваться всеми абонентами сети). Затем каждый абонент группы выбирает свое секретное число ci, 1 < Ci < р - 1, и вычисляет соответствующее ему открытое число di, di=gcimodp результате получаем таблицу. Таблица. Ключи пользователей в системе Эль-Гамаля
Покажем теперь, как А передает сообщение т абоненту В. Будем предполагать, как и при описании шифра Шамира, что сообщение представлено в виде числа m < р. Шаг 1. А формирует случайное число к, 1 r = gk mod p, e = m и передает пару чисел (r, е) абоненту В.
Шаг 2. В, получив (r,е), вычисляет m' Утверждение (свойства шифра Эль-Гамаля), 1) Абонент В получил сообщение, т.е. m/=m; 2) противник, зная р, g, dB, r и е, не может вычислить m. Доказательство. Подставим в (3.4) значение е из (3.3): m' = m Теперь вместо r подставим (3.2), а вместо dB - (3.1): m' = m По теореме Ферма gk(p-1)mod p=1kmod p = 1 и таким образом, мы получаем первую часть утверждения. Для доказательства второй части заметим, что противник не может вычислить k в равенстве (3.2), так как это задача дискретного логарифмирования. Следовательно, он не может' вычислить m в равенстве (3.3), так как m было умножено на неизвестное ему чисто Противник также не может воспроизвести действия законного получателя сообщения (абонента В), так как ему не известно секретное число св (вычисление св на основании (3.1) - также задача дискретного логарифмирования). Идентификация и проверка подлинности. Применение пароля. Основные понятия. Идентификацию и аутентификацию можно считать основой программно-технических средств безопасности, поскольку остальные сервисы рассчитаны на обслуживание именованных субъектов. Идентификация и аутентификация – это первая линия обороны, "проходная" информационного пространства организации. Идентификация позволяет субъекту (пользователю, процессу, действующему от имени определенного пользователя, или иному аппаратно-программному компоненту) назвать себя (сообщить свое имя). Посредством аутентификации вторая сторона убеждается, что субъект действительно тот, за кого он себя выдает. В качестве синонима слова "аутентификация" иногда используют словосочетание "проверка подлинности". Аутентификация бывает односторонней (обычно клиент доказывает свою подлинность серверу) и двусторонней (взаимной). Пример односторонней аутентификации – процедура входа пользователя в систему. В сетевой среде, когда стороны идентификации/аутентификации территориально разнесены, у рассматриваемого сервиса есть два основных аспекта: - что служит аутентификатором (то есть используется для подтверждения подлинности субъекта); - как организован (и защищен) обмен данными идентификации/аутентификации. Субъект может подтвердить свою подлинность, предъявив по крайней мере одну из следующих сущностей: - нечто, что он знает (пароль, личный идентификационный номер, криптографический ключ и т.п.); - нечто, чем он владеет (личную карточку или иное устройство аналогичного назначения);
- нечто, что есть часть его самого (голос, отпечатки пальцев и т.п., то есть свои биометрические характеристики). Парольная аутентификация. Главное достоинство парольной аутентификации – простота и привычность. Пароли давно встроены в операционные системы и иные сервисы. При правильном использовании пароли могут обеспечить приемлемый для многих организаций уровень безопасности. Тем не менее, по совокупности характеристик их следует признать самым слабым средством проверки подлинности. Следующие меры позволяют значительно повысить надежность парольной защиты: - наложение технических ограничений (пароль должен быть не слишком коротким, он должен содержать буквы, цифры, знаки пунктуации и т.п.); - управление сроком действия паролей, их периодическая смена; - ограничение доступа к файлу паролей; - ограничение числа неудачных попыток входа в систему (это затруднит применение "метода грубой силы"); - обучение пользователей; - использование программных генераторов паролей (такая программа, основываясь на несложных правилах, может порождать только благозвучные и, следовательно, запоминающиеся пароли). - Перечисленные меры целесообразно применять всегда, даже если наряду с паролями используются другие методы аутентификации. Электронно-цифровая подпись Электро́нная цифровая по́дпись (ЭЦП) — информация в электронной форме, присоединенная к другой информации в электронной форме (электронный документ) или иным образом связанная с такой информацией. Используется для определения лица, подписавшего информацию (электронный документ) По своему существу электронная подпись представляет собой реквизит электронного документа, позволяющий установить отсутствие искажения информации в электронном документе с момента формирования ЭП и проверить принадлежность подписи владельцу сертификата ключа ЭП. Значение реквизита получается в результате криптографического преобразования информации с использованием закрытого ключа ЭП. Электронная подпись предназначена для идентификации лица, подписавшего электронный документ и является полноценной заменой (аналогом) собственноручной подписи в случаях, предусмотренных законом Использование электронной подписи позволяет осуществить: - Контроль целостности передаваемого документа: при любом случайном или преднамеренном изменении документа подпись станет недействительной, потому что вычислена она на основании исходного состояния документа и соответствует лишь ему. - Защиту от изменений (подделки) документа: гарантия выявления подделки при контроле целостности делает подделывание нецелесообразным в большинстве случаев. - Невозможность отказа от авторства. Так как создать корректную подпись можно, лишь зная закрытый ключ, а он должен быть известен только владельцу, то владелец не может отказаться от своей подписи под документом. - Доказательное подтверждение авторства документа: Так как создать корректную подпись можно, лишь зная закрытый ключ, а он должен быть известен только владельцу, то владелец пары ключей может доказать своё авторство подписи под документом. В зависимости от деталей определения документа могут быть подписаны такие поля, как «автор», «внесённые изменения», «метка времени» и т. д.
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 698; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.190.43 (0.013 с.) |

 называется разложение его на простые сомножители в виде
называется разложение его на простые сомножители в виде  , где
, где  - все различные простые делители числа
- все различные простые делители числа  - целые положительные числа.
- целые положительные числа. ,
,
 - каноническое разложение
- каноническое разложение 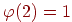 ,
,  ,
, 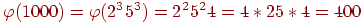 .
. называются взаимно простыми, если у них нет общих делителей больших 1, т.е.
называются взаимно простыми, если у них нет общих делителей больших 1, т.е.  .
. [6].
[6]. равно
равно  [12].
[12]. имеет место соотношение
имеет место соотношение  .
. , где
, где  , можно использовать теорему Эйлера-Ферма, т.е.
, можно использовать теорему Эйлера-Ферма, т.е.  , но это весьма трудоемкий способ. Получим решения искомого уравнения через формулу для решения эквивалентного уравнения
, но это весьма трудоемкий способ. Получим решения искомого уравнения через формулу для решения эквивалентного уравнения  .
.
 - остатки. Разложение
- остатки. Разложение  в цепную дробь по последовательности частных
в цепную дробь по последовательности частных

 дробь, получаемую из приведенной цепной дроби отбрасыванием членов с индексами, большими
дробь, получаемую из приведенной цепной дроби отбрасыванием членов с индексами, большими  . Например,
. Например,  ,
,  и т.д. Числитель,
и т.д. Числитель,  , и знаменатель,
, и знаменатель,  , можно вычислять рекуррентно по следующим формулам:
, можно вычислять рекуррентно по следующим формулам:

 и
и  . Кроме того,
. Кроме того,




 и
и  .
.
 . Сначала по алгоритму Евклида получается следующая цепочка соотношений:
. Сначала по алгоритму Евклида получается следующая цепочка соотношений: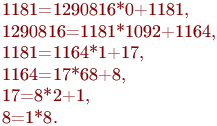

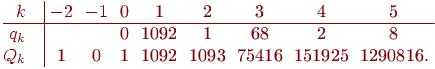
 равен 151925.
равен 151925.

 , доказывается индукцией по m.
, доказывается индукцией по m. .
.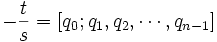 .
.

 р, то сообщение предствляется в виде m1, m2,..., mt, где все mi < р, и затем передаются последовательно m1, m2,..., mt. При этом для кодирования каждого mi лучше выбирать случайно новые пары (cA,dA) и (cB,dB) — в противном случае надежность системы понижается. В настоящее время такой шифр, как правило, используется для передачи чисел, например, секретных ключей, значения которых меньше р. Таким образом, мы будем рассматривать только случай m < р.
р, то сообщение предствляется в виде m1, m2,..., mt, где все mi < р, и затем передаются последовательно m1, m2,..., mt. При этом для кодирования каждого mi лучше выбирать случайно новые пары (cA,dA) и (cB,dB) — в противном случае надежность системы понижается. В настоящее время такой шифр, как правило, используется для передачи чисел, например, секретных ключей, значения которых меньше р. Таким образом, мы будем рассматривать только случай m < р.
 к
к  р-2, вычисляет числа
р-2, вычисляет числа dBk mod p
dBk mod p = е
= е 


