
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Информация как объект юридической и физической защиты.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Информация как объект юридической и физической защиты. Юридические меры защиты информации обладают рядом признаков, которые отличают их от прочих видов защиты данных: организационных, физических, технических. Юридические средства защиты не могут физически схватить за руку злоумышленника или преградить ему доступ к секретам фирмы. Юридические средства выполняют особые функции, позволяющие им занимать свое особое место в корпоративной системе защиты информации. С одной стороны, юридические меры выполняют охранительную функцию. Они формируют отношение субъектов оборота информации к нормам и правилам такого оборота: «Не нарушай! За нарушение накажут по всей строгости Закона». С другой стороны − компенсационная функция: в случае нанесения вреда законному владельцу информации Закон привлекает нарушителя к ответственности и обязывает его возместить причиненный ущерб.
Основные цели и задачи обеспечения безопасности информации в ТКС Уязвимость ТКС - это некоторое неудачное свойство системы, которое делает возможным возникновение и реализацию угрозы. Атака на компьютерную систему-это действие, предпринимаемое злоумышленником, которое заключается в поиске и использовании той или иной уязвимости системы. Таким образом, атака-это реализация угрозы безопасности. Противодействие угрозам безопасности является целью защиты систем обработки информации. Под угрозой безопасности информации будем понимать возникновение такого явления или события, следствием которого могут быть негативные воздействия на информацию: нарушение физической целостности, логической структуры, несанкционированная модификация несанкционированное получение, несанкционированное размножение. Объектом исследования является информация, передаваемая по телекоммуникационным сетям. Предметом исследования является информационная безопасность телекоммуникационных сетей. По цели воздействия различают три основных типа угроз безопасности ТКС: • угрозы нарушения конфиденциальности информации; • угрозы нарушения целостности информации; • угрозы нарушения работоспособности системы (отказы в обслуживании) Угрозы нарушения конфиденциальности направлены на разглашение конфиденциальной или секретной информации. Угрозы нарушения целостности информации, хранящейся в компьютерной системе или передаваемой по каналу связи, направлены на ее изменение или искажение, приводящее к нарушению ее качества или полному уничтожению. Целостность информации может быть нарушена умышленно злоумышленником, а также в результате объективных воздействий со стороны среды, окружающей систему.
Угрозы нарушения раоотоспосооности направлены на создание таких ситуаций, когда определенные преднамеренные действия либо снижают работоспособность ТКС, либо блокируют доступ к некоторым ее ресурсам.
3. Архитектура телекоммуникационных систем. Классифицируя сети по территориальному признаку, различают локальные (LAN), глобальные (WAN) и городские (MAN) сети. В зависимости от масштаба производственного подразделения, в пределах которого действует сеть, различают сети отделов, сети кампусов и корпоративные сети.
Сети отделов используются небольшой группой сотрудников в основном с целью разделения дорогостоящих периферийных устройств, приложений и данных; имеют один-два файловых сервера и не более тридцати пользователей; обычно не разделяются на подсети; создаются на основе какой-либо одной сетевой технологии; могут работать на базе одноранговых сетевых ОС. Сети кампусов объединяют сети отделов в пределах отдельного здания или одной территории площадью в несколько квадратных километров, при этом глобальные соединения не используются. На уровне сети кампуса возникают проблемы интеграции и управления неоднородным аппаратным и программным обеспечением. Корпоративные сети объединяют большое количество компьютеров на всех территориях отдельного предприятия. Для корпоративной сети характерны: масштабность — тысячи пользовательских компьютеров, сотни серверов, огромные объемы хранимых и передаваемых по линиям связи данных, множество разнообразных приложений; Угрозы информационной безопасности. По данным исследования, превалирующими по объему потерь преступлениями в информационной сфере за 2005 год являются: распространение вирусов (42,8 млн. долл.), неавторизованный доступ (31,2 млн. долл.),
кража конфиденциальной информации (30,9 млн. долл.).
Цели и возможные сценарии несанкционированного доступа в ТКС. Несанкционированный доступ. В вычислительной технике понятие безопасности является весьма широким. Оно подразумевает и надежность работы компьютера, и сохранность ценных данных, и защиту информации от внесения в нее изменений неуполномоченными лицами, и сохранение тайны переписки в электронной связи. Разумеется, во всех цивилизованных странах на безопасности граждан стоят законы, но в вычислительной техники правоприменительная практика пока не развита, а законотворческий процесс не успевает за развитием технологий, и надежность работы компьютерных систем во многом опирается на меры самозащиты.
Способы хищения информации. Проблема безопасности информации трудно решаема в силу двух причин. Во-первых, способы хищения информации постоянно усложняются. Во-вторых, владельцы информации относятся к ее защите легкомысленно. Как правило, устанавливается одна или две стандартных программы, которые на практике не соответствуют уровню потенциальной опасности. Через интернет или любой носитель информации (CD с программным обеспечением) Ваш компьютер подвергается атаке вирусов и «программ-шпионов». С вирусами справляются многочисленные антивирусные программы. Большую опасность несут программы-шпионы. Они способны не только считать и передать файлы с конфиденциальной информацией, но и отследить все Ваши действия на компьютере. Программы-шпионы запоминают посещаемые Вами сайты, регистрируют нажатия на клавиатуру (так рассекречивают номера кредитных карт и pin-коды), позволяют нелегально подключаться к сети через Ваш компютер. Другой источник опасности — сам факт выхода в нтернет. IP-адрес Вашего компьютера может быть зафиксирован любым интернет-ресурсом. IP-адрес соотносится с Вашими персональными (паспортными) данными в базе провайдера. Соответственно, тот, кто обладает Вашими персональными данными и сведениями о посещаемых Вами ресурсах, может использовать эту информацию во вред Вашей компании, имиджу и финансовому положению. Отслеживание IP-адреса пресекалось использованием прокси-серверов и сайтов-анонимайзеров. Однако 1 июля 2006 года были приняты новые «Правила оказания услуг связи по передаче данных». Согласно им, в базу данных вносится любой пользователь интернета, а также информация о посещаемых им сайтах. База данных, доступная ФСБ и МВД, позволяет контролировать не только злоумышленников, но и рядовых пользователей. Серьезную угрозу представляют хакеры. Согласно ежедневным сообщениям СМИ о хищении информации, объектом взлома может стать компьютер и частного пользователя, и крупной организации. Методы сложной замены Шифр сложной замены, называемый шифром Грансфельда, представляет собой модификацию шифра Цезаря числовым ключом. Для этого под буквами исходного сообщения записывают цифры числового ключа. Если ключ короче сообщения, то его запись циклически повторяют. Шифртекст получают примерно, как в шифре Цезаря, но отсчитывают по алфавиту не третью букву (как это делается в шифре Цезаря), а выбирают ту букву, которая смещена па алфавиту на соответствующую цифру ключа. Например, применяя в качестве ключа группы из четырех начальных цифр числа е (основная натуральных логарифмов), а именно 2718, получаем для исходного сообщения ВОСТОЧНЫЙ ЭКСПРЕСС следующий шифртексты:
Сообщения В О С Т О Ч Н Ы Й Э К С П Р Е С С Ключ 2 7 1 8 2 7 1 8 2 7 1 8 2 7 1 8 2 Шифртекст Д Х Т Ь Р Ю О Г Л Д Л Щ С Ч Ж Щ У Чтобы зашифровать первую букву сообщения В, используя первую цифру ключа 2, нужно отсчитать вторую по порядку букву от В в алфавите В-Г-Д; получается первая буква шифртекста Д. Следует отметить, что шифр Гронсфельда вскрывается относительно легко, если учесть, что в числовом ключе каждая цифра имеет только десять значений, а значит, имеется лишь десять вариантов прочтения каждой буквы шифртекста. С другой стороны, шифр Гронсфельда допускает дальнейшие модификации, улучшающие его стойкость, в частности двойное шифрование разными числовыми ключами. Шифр Гронсфельда представляет собой по существу частный случай системы шифрования Вижинера.
Система шифрования Цезаря. Шифр Цезаря основан на фиксированном смещении по кругу букв алфавита. Буквы сдвигаются по кругу, так что после последней буквы алфавита идет его первая буква. В следующем листинге (на языке java) приводится алгоритм шифрования на основе шифра Цезаря. При шифровании с ключом алгоритмы шифрования и расшифровки могут быть хорошо известны. Но дешифровальный и (иногда) шифровальный ключи строго секретны. Зашифрованный текст, полученный в результате шифрования открытого текста с помощью конкретного шифровального ключа, может быть расшифрован только с помощью дешифровального ключа, связанного с шифровальным ключом. В шифре Цезаря ключи представляют собой число символов, на которое сдвигаются буквы алфавита. При шифровании вместо каждой буквы открытого текста ставится буква отстоящая от нее вправо на число букв задаваемое значением ключа. Расшифровка заключается в смещении каждой буквы влево на число букв, задаваемое тем же значением ключа, которое использовалось при шифровании. (То есть decryptKey = -encrypKey) Не нужно быть опытным дешифровальщиком, чтобы понять, что Шифр Цезаря обладает низкой стойкостью. В нем (в случае русского алфавита) возможны всего 32 различных ключей, один из которых отображает открытый текст в тот же открытый текст. Это дает представление о размере пространства ключей. Пространство ключей шифра – это набор всех возможных ключей, которые работаю с этим шифром. Чтобы шифр был эффективным, пространство ключей должно быть большим. Размер пространства ключей обычно измеряется числом двоичных разрядов ключа. В n-битном пространстве ключей возможны 2n разных ключа. Для 32-х-битного ключа это число составляет 4 294 967 296 разных ключей. Хотя такое число может показаться большим, на самом деле оно достаточно мало. Средней мощности компьютер может за день “перепробовать” 4 миллиарда ключей.
Шифр Вернамана. Система шифрования Вернама является в сущности частным случаем системы шифрования Вижинера при значении модуля m -2. Конкретная версия этого шифра использует двоичное представление символов исходного текста. Каждый символ исходного открытого текста из английского алфавита {А, В, С, D,..., Z}, расширенного шестью вспомогательными символами (пробел, возврат каретки и т.п.), сначала кодировался в 5-битовый блок (bo, b1..., Ь4) телеграфного кода Бодо. Случайная последовательность двоичных ключей k0, k1, k2,... заранее записывалась на бумажной ленте. Схема передачи сообщений с использованием шифрования методом Вернама показана на рис. 2.11. Шифрование исходного текста, предварительно преобразованного в последовательность двоичных символов х, осуществлялось путем сложения по модулю 2 символов х с последовательностью двоичных ключей k. Символы шифртекста
Рис. 2.11. Схема шифрования и расшифрования сообщений по методу Вернама Расшифрование состоит в сложении по модулю 2 символов у.шифртекста с той же последовательностью ключей k:
При этом последовательности ключей, использованные при шифровании и расшифровании, компенсируют друг друга (при сложении по модулю 2), и в результате восстанавливаются символы х исходного текста. При разработке своей системы Вернам проверял ее с помощью закольцованных лент, установленных на передатчике и приемнике для того, чтобы использовалась одна и та же последовательность ключей. Следует отметить, что метод Вернама не зависит от длины последовательности ключей и, кроме того, он позволяет использовать случайную последовательность ключей. Однако при реализации метода Вернама возникают серьезные проблемы, связанные с.необходимостью доставки получателю такой же последовательности ключей, как у отправителя, либо с необходимостью безопасного хранения идентичных последовательностей ключей у отправителя и получателя. Эти недостатки системы шифрования Вернама преодолены при шифровании методом гаммирования.
Рассеивание и перемешивание На практике обычно используют два общих принципа шифрования: рассеивание и перемешивание. Рассеивание заключается в распространении влияния одного символа открытого текста на много символов шифртекста: это позволяет скрыть статистические свойства открытого текста. Развитием этого принципа является распространение влияния одного символа ключа на много символов шифрограммы, что позволяет исключить восстановление ключа по частям. Перемешивание состоит в использовании таких шифрующих преобразований, которые исключают восстановление взаимосвязи статистических свойств открытого и шифрованного текста. Распространенный способ достижения хорошего рассеивания состоит в использовании составного шифра, который может быть реализован в виде некоторой последовательности простых шифров, каждый из которых вносит небольшой вклад в значительное суммарное рассеивание и перемешивание. В качестве простых
шифров чаще всего используют простые подстановки и перестановки. Одним из наилучших примеров криптоалгоритма, разработанного в соответствии с принципами рассеивания и перемешивания, может служить принятый в 1977 году Национальным бюро стандартов США стандарт шифрования данных DES. Несмотря на интенсивные и тщательные исследования алгоритма специалистами, пока не найдено уязвимых мест алгоритма, на основе которых можно было бы предложить метод криптоанализа, существенно лучший, чем полный перебор ключей. Алгоритм шифрования DEA Исходные идеи алгоритма шифрования данных DEA (data encryption algorithm) были предложены компанией IBM еще в 1960-х годах и базировались на идеях, описанных Клодом Шенноном в 1940-х годах. Первоначально эта методика шифрования называлась lucifer (разработчик Хорст Фейштель, название dea (см. http/:snoopy.falkor.gen.nz/~rae/des.html) она получила лишь в 1976 году. Lucifer был первым блочным алгоритмом шифрования, он использовал блоки размером 128 бит и 128-битовый ключ. По существу этот алгоритм являлся прототипом DEA. В 1986 в Японии (NIT) разработан алгоритм FEAL(Fast data Encipherment ALgorithm), предназначенный для использования в факсах, модемах и телефонах (длина ключа до 128 бит). Существует и ряд других разработок. DEA оперирует с блоками данных размером 64 бита и использует ключ длиной 56 бит. Такая длина ключа соответствует 1017 комбинаций, что обеспечивало до недавнего времени достаточный уровень безопасности. В дальнейшем можно ожидать расширения ключа до 64 бит (например, LOKI) или вообще замены DES другим стандартом. Входной блок данных, состоящий из 64 бит, преобразуется в выходной блок идентичной длины. Ключ шифрования должен быть известен, как отправляющей так и принимающей сторонам. В алгоритме широко используются перестановки битов текста. Вводится функция f, которая работает с 32-разрядными словами исходного текста (А) и использует в качестве параметра 48-разрядный ключ (J). Схеме работы функции f показана на рис. 6.4.1.1. Сначала 32 входные разряда расширяются до 48, при этом некоторые разряды повторяются. Схема этого расширения показана ниже (номера соответствуют номерам бит исходного 32-разрядного кода).
Блочные и поточные шифры. Практически все применяемые криптографические методы связаны с разбиением сообщения на большое число фрагментов (или знаков) фиксированного размера, каждый из которых шифруется отдельно. Такой подход существенно упрощает задачу шифрования, так как сообщения обычно имеют различную длину. Различают три основных способа шифрования: поточные шифры, блочные шифры и блочные шифры с обратной связью. Поточное шифрование состоит в том, что биты открытого текста складываются по модулю 2 с битами псевдослучайной последовательности. К достоинствам поточных шифров относятся высокая скорость шифрования, относительная простота реализации и отсутствие размножения ошибок. Недостатком является необходимость передачи информации синхронизации перед заголовком сообщения, которая должна быть принята до расшифрования любого сообщения. Поточные шифры широко применяются для шифрования преобразованных в цифровую форму речевых сигналов и цифровых данных, требующих оперативной доставки потребителю информации. Стандартным методом генерирования последовательностей для поточного шифрования является метод, применяемый в стандарте шифрования DES в режиме обратной связи по выходу (режим OFB). При блочном шифровании открытый текст сначала разбивается на равные по длине блоки, затем применяется зависящая от ключа функция шифрования для преобразования блока открытого текста длиной m бит в блок шифртекста такой же длины. Достоинством блочного шифрования является то, что каждый бит блока шифртекста зависит от значений всех битов соответствующего блока открытого текста, и никакие два блока открытого текста не могут быть представлены одним и тем же блоком шифртекста. Алгоритм блочного шифрования может использоваться в различных режимах. Четыре режима шифрования алгоритма DES фактически применимы к любому блочному шифру: Electronic code Book, Cipher block chaining, Cipher feedback Output feedback.
Однонаправленные функции Понятие однонаправленной функции является основным в криптографии с открытым ключом. К однонаправленным относят такие функции, которые достаточно легко вычислить, но значительно труднее обратить. То есть, при наличии х нетрудно определить f(x), однако, при условии знания только f(x) на нахождение соответствующего значения х уйдут миллионы лет вычислений на всех компьютерах, которые только есть в мире. Аналогом однонаправленной функции в быту является разбитая вдребезги стеклянная бутылка. Расколотить ее на мелкие осколки очень легко, однако попробуйте снова собрать целую бутылку из осколков! Строгое математическое доказательство существования однонаправленных функций, а также правила их построения пока не придуманы. Тем не менее. существует множество функций, которые все считают однонаправленными: их значения довольно эффективно вычисляются, однако обратить эти функции каким-либо простым методом не удается. Хорошим примером может служить вычисление функции х 2 в конечных полях. Какой прок от однонаправленных функций в криптографии? Ведь если с ее помощью зашифровать сообщение, прочесть его не сможет никто. Вернемся к аналогии с бутылкой. Напишите на ней открытый текст, разбейте ее вдребезги и дайте осколки своему приятелю, чтобы он прочитал написанный вами текст. И не забудьте упомянуть про однонаправленные функции, чтобы произвести на него должное впечатление вашими глубокими познаниями в криптографии! К сожалению, дальнейший путь этих осколков лежит только в мусорное ведро, ибо в таком виде ваше послание не примет ни одно почтовое отделение. Поэтому в криптографии большим спросом пользуются однонаправленные функции с лазейкой, которые представляют собой особую разновидность однонаправленных функций. Однонаправленную функцию с лазейкой по-прежнему трудно обратить, но только не зная секрета вычисления обратной к ней функции. То есть, при данном х легко найти f(x) и наоборот — трудно отыскать х, зная одно лишь значение f(x). Однако существует такая секретная информация (у), что если известны у и f(x), то вычислить х будет значительно проще. Хорошим аналогом однонаправленной функции с лазейкой служат обыкновенные часы. Их очень легко разобрать на большое количество мельчайших деталей, из которых потом будет весьма трудно снова собрать работающий часовой механизм. Однако при наличии инструкции по сборке часов сделать это не так и сложно.
Особый интерес для криптографов представляют однонаправленные хэш-функции. Алгоритмы хэширования, реализуемые с помощью хэш-функций, позволяют преобразовывать строки переменной длины, называемые образами, в строки фиксированной длины, которые принято именовать хэш-значениями. Обычно хэш-значение гораздо меньше любого из образов. Примером простейшей хэш-функции является преобразование байтовой строки в хэш-значение, равное одному байту, который получается сложением всех байтов этой строки по модулю 2. Однако такая кэш-функция не является однонаправленной: нетрудно подобрать строку символов, суммирование которых по модулю 2 даст заранее заданное значение. Однонаправленная хэш-функция позволяет легко сгенерировать, хэш-значение. Однако, зная только его, будет очень трудно подобрать соответствующий ему образ. Качественная однонаправленная хэш-функция чаше всего является непротиворечивой: весьма сложно получить два различных образа, для которых хэш-значение будет одним и тем же.Процесс хэширования в криптографии — не тайна. Однонаправленная хэш- функция обеспечивает необходимый уровень зашиты благодаря своей однонаправленности. По выходу такой хэш-функции невозможно сказать, что было подано на ее вход, а изменение даже одного бита образа приводит к смене в среднем половины бит соответствующего хэш-значения. Алгоритм Евклида Пусть a и b суть целые числа, не равные одновременно нулю, и последовательность чисел
определена тем, что каждое rk это остаток от деления пред-предыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, т. е. a = bq 0 + r 1 b = r 1 q 1 + r 2 r 1 = r 2 q 2 + r 3
rn − 1 = rnqn Тогда (a, b), наибольший общий делитель a и b, равен rn, последнему ненулевому члену этой последовательности. Существование таких r 1, r 2,..., то есть возможность деления с остатком m на n для любого целого m и целого Корректность этого алгоритма вытекает из следующих двух утверждений: · Пусть a = bq + r, тогда (a, b) = (b, r). · (0, r) = r. для любого ненулевого r. Связь с цепными дробями · Отношение a / b допускает представление в виде цепной дроби:
· Отношение - t / s, в расширенном алгоритме Евклида допускает представление в виде цепной дроби:
Ускоренные версии алгоритма Алгоритм может быть записан в общем виде не только для целых чисел, но и для полиномов. Строго говоря, алгоритм работает в любом евклидовом кольце. Одним из методов ускорения целочисленного алгоритма Евклида является выбор симметричного остатка: · причем · Одна из наиболее многообещающих версий ускоренного алгоритма Евклида для полиномов основывается на том, что промежуточные значения алгоритма в основном зависят от высоких степеней. При применении стратегии Divide & Conqurer наблюдается большое ускорение асимптотической скорости алгоритма. Шифр Шамира Этот шифр, предложенный Шамиром {Adi Shamir), был первым, позволяющим организовать обмен секретными сообщениями по открытой линии связи для лиц, которые не имеют никаких защищенных каналов и секретных ключей и, возможно, никогда не видели друг друга. (Напомним, что система Диффи-Хеллмана позволяет сформировать только секретное слово, а передача сообщения потребует использования некоторого шифра, где это слово будет использоваться как ключ.) Перейдем к описанию системы. Пусть есть два абонента Аи В, соединенные линией связи. А хочет передать сообщение m абоненту Б так, чтобы никто не узнал его содержание. А выбирает случайное большое простое число р и открыто передает его В. Затем А выбирает два числа сА и dA, такие, что сАdA mod (р - 1) = 1. Эти числа А держит в секрете и передавать не будет. В тоже выбирает два числа св dв, такие, что и держит их в секрете. св<dв mod (p - 1) = 1, После этого А передает свое сообщение m, используя трехступенчатый протокол. Если m < р (m рассматривается как число), то сообщение т передается сразу, если же т Описание протокола. Шаг 1. А вычисляет число Х1 =mСА modp где m — исходное сообщение, и пересылает х1 к В. Шаг 2. В, получив х1, вычисляет число X2 = х2CB mod p и передает х2 к А. Шаг 3. А вычисляет число X3 = х2dA mod p и передает его В. Шаг 4. В, получив х3, вычисляет число X4 = x3dB mod p. Шифр Эль-Гамаля Пусть имеются абоненты А, В, С,..., которые хотят передавать друг другу зашифрованные сообщения, не имея никаких защищенных каналов связи. Эль-Гамаль (Tahcr ElGamal), который решает эту задачу, используя, в отличие от шифра Шамира, только одну пересылку сообщения. Фактически здесь используется схема Диффи-Хеллмана, чтобы сформировать общий секретный ключ для двух абонентов, передающих друг другу сообщение, и затем сообщение шифруется путем умножения его на этот ключ. Для каждого следующего сообщения секретный ключ вычисляется заново. Перейдем к точному описанию метода. Для всей группы абонентов выбираются некоторое большое простое число р и число g, такие, что различные степени g суть различные числа по модулю р.Числа р и g передаются абонентам в открытом виде (они могут использоваться всеми абонентами сети). Затем каждый абонент группы выбирает свое секретное число ci, 1 < Ci < р - 1, и вычисляет соответствующее ему открытое число di, di=gcimodp результате получаем таблицу. Таблица. Ключи пользователей в системе Эль-Гамаля
Покажем теперь, как А передает сообщение т абоненту В. Будем предполагать, как и при описании шифра Шамира, что сообщение представлено в виде числа m < р. Шаг 1. А формирует случайное число к, 1 r = gk mod p, e = m и передает пару чисел (r, е) абоненту В. Шаг 2. В, получив (r,е), вычисляет m' Утверждение (свойства шифра Эль-Гамаля), 1) Абонент В получил сообщение, т.е. m/=m; 2) противник, зная р, g, dB, r и е, не может вычислить m. Доказательство. Подставим в (3.4) значение е из (3.3): m' = m Теперь вместо r подставим (3.2), а вместо dB - (3.1): m' = m По теореме Ферма gk(p-1)mod p=1kmod p = 1 и таким образом, мы получаем первую часть утверждения. Для доказательства второй части заметим, что противник не может вычислить k в равенстве (3.2), так как это задача дискретного логарифмирования. Следовательно, он не может' вычислить m в равенстве (3.3), так как m было умножено на неизвестное ему чисто Противник также не может воспроизвести действия законного получателя сообщения (абонента В), так как ему не известно секретное число св (вычисление св на основании (3.1) - также задача дискретного логарифмирования). Идентификация и проверка подлинности. Применение пароля. Основные понятия. Идентификацию и аутентификацию можно считать основой программно-технических средств безопасности, поскольку остальные сервисы рассчитаны на обслуживание именованных субъектов. Идентификация и аутентификация – это первая линия обороны, "проходная" информационного пространства организации. Идентификация позволяет субъекту (пользователю, процессу, действующему от имени определенного пользователя, или иному аппаратно-программному компоненту) назвать себя (сообщить свое имя). Посредством аутентификации вторая сторона убеждается, что субъект действительно тот, за кого он себя выдает. В качестве синонима слова "аутентификация" иногда используют словосочетание "проверка подлинности". Аутентификация бывает односторонней (обычно клиент доказывает свою подлинность серверу) и двусторонней (взаимной). Пример односторонней аутентификации – процедура входа пользователя в систему. В сетевой среде, когда стороны идентификации/аутентификации территориально разнесены, у рассматриваемого сервиса есть два основных аспекта: - что служит аутентификатором (то есть используется для подтверждения подлинности субъекта); - как организован (и защищен) обмен данными идентификации/аутентификации. Субъект может подтвердить свою подлинность, предъявив по крайней мере одну из следующих сущностей: - нечто, что он знает (пароль, личный идентификационный номер, криптографический ключ и т.п.); - нечто, чем он владеет (личную карточку или иное устройство аналогичного назначения); - нечто, что есть часть его самого (голос, отпечатки пальцев и т.п., то есть свои биометрические характеристики). Парольная аутентификация. Главное достоинство парольной аутентификации – простота и привычность. Пароли давно встроены в операционные системы и иные сервисы. При правильном использовании пароли могут обеспечить приемлемый для многих организаций уровень безопасности. Тем не менее, по совокупности характеристик их следует признать самым слабым средством проверки подлинности. Следующие меры позволяют значительно повысить надежность парольной защиты: - наложение технических ограничений (пароль должен быть не слишком коротким, он должен содержать буквы, цифры, знаки пунктуации и т.п.); - управление сроком действия паролей, их периодическая смена; - ограничение доступа к файлу паролей; - ограничение числа неудачных попыток входа в систему (это затруднит применение "метода грубой силы"); - обучение пользователей; - использование программных генераторов паролей (такая программа, основываясь на несложных правилах, может порождать только благозвучные и, следовательно, запоминающиеся пароли). - Перечисленные меры целесообразно применять всегда, даже если наряду с паролями используются другие методы аутентификации. Электронно-цифровая подпись Электро́нная цифровая по́дпись (ЭЦП) — информация в электронной форме, присоединенная к другой информации в электронной форме (электронный документ) или иным образом связанная с такой информацией. Используется для определения лица, подписавшего информацию (электронный документ) По своему существу электронная подпись представляет собой реквизит электронного документа, позволяющий установить отсутствие искажения информации в электронном документе с момента формирования ЭП и проверить принадлежность подписи владельцу сертификата ключа ЭП. Значение реквизита получается в результате криптографического преобразования информации с использованием закрытого ключа ЭП. Электронная подпись предназначена для идентификации лица, подписавшего электронный документ и является полноценной заменой (аналогом) собственноручной подписи в случаях, предусмотренных законом Использование электронной подписи позволяет осуществить: - Контроль целостности передаваемого документа: при любом случайном или преднамеренном изменении документа подпись станет недействительной, потому что вычислена она на основании исходного состояния документа и соответствует лишь ему. - Защиту от изменений (подделки) документа: гарантия выявления подделки при контроле целостности делает подделывание нецелесообразным в большинстве случаев. - Невозможность отказа от авторства. Так как создать корректную подпись можно, лишь зная закрытый ключ, а он должен быть известен только владельцу, то владелец не может отказаться от своей подписи под документом. - Доказательное подтверждение авторства документа: Так как создать корректную подпись можно, лишь зная закрытый ключ, а он должен быть известен только владельцу, то владелец пары ключей может доказать своё авторство подписи под документом. В зависимости от деталей определения документа могут быть подписаны такие поля, как «автор», «внесённые изменения», «метка времени» и т. д. Накопление ключей Под накоплением ключей понимается организация их хранения, учета и удаления. Поскольку ключ является самым привлекательным для злоумышленника объектом, открывающим ему путь к конфиденциальной информации, то вопросам накопления ключей следует уделять особое внимание. Секретные ключи никогда не должны записываться в явном виде на носителе, который может быть считан или скопирован. В достаточно сложной ИС один пользователь может работать с большим объемом ключевой информации, и иногда даже возникает необходимость организации мини-баз данных по ключевой информации. Такие базы данных отвечают за принятие, хранение, учет и удаление используемых ключей. Итак, каждая информация об используемых ключах должна храниться в зашифрованном виде. Ключи, зашифровывающие ключевую информацию называются мастер-ключами. Желательно, чтобы мастер-ключи каждый пользователь знал наизусть, и не хранил их вообще на каких-либо материальных носителях. Очень важным условием безопасности информации является периодическое обновление ключевой информации в ИС. При этом переназначаться должны как обычные ключи, так и мастер-ключи. В особо ответственных ИС обновление ключевой информации желательно делать ежедневно.
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 688; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.223.129 (0.024 с.) |


 (2.13)
(2.13)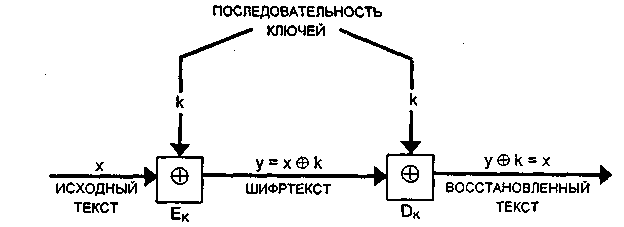
 (2.14)
(2.14)

 , доказывается индукцией по m.
, доказывается индукцией по m. .
.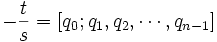 .
.

 р, то сообщение предствляется в виде m1, m2,..., mt, где все mi < р, и затем передаются последовательно m1, m2,..., mt. При этом для кодирования каждого mi лучше выбирать случайно новые пары (cA,dA) и (cB,dB) — в противном случае надежность системы понижается. В настоящее время такой шифр, как правило, используется для передачи чисел, например, секретных ключей, значения которых меньше р. Таким образом, мы будем рассматривать только случай m < р.
р, то сообщение предствляется в виде m1, m2,..., mt, где все mi < р, и затем передаются последовательно m1, m2,..., mt. При этом для кодирования каждого mi лучше выбирать случайно новые пары (cA,dA) и (cB,dB) — в противном случае надежность системы понижается. В настоящее время такой шифр, как правило, используется для передачи чисел, например, секретных ключей, значения которых меньше р. Таким образом, мы будем рассматривать только случай m < р.
 к
к  р-2, вычисляет числа
р-2, вычисляет числа dBk mod p
dBk mod p = е
= е 


