
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные символы блок-схем алгоритмовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Терминатор (пуск-останов): начальный символ означает начало алгоритма, конечный – его конец. вход вход
выход выход 2. Процесс: вычислительный символ означает выполнение одной операции или группы операций обработки данных, где операция является некоторой командой, называемой оператором. вход вход выход вход выход
выход 3. Решение:условный символ означает выбор направления выполнения алгоритма в зависимости от логического условия, которое может принимать только два значении: «1» («+»), если условие выполняется (да), «0» («–»), если условие не выполняется (нет). вход 1 (да)
завершения
цикла
выход или
завершения,
выход 5. Подготовка: символ отображает модификацию команды или группы команд; можно использовать как символ структуры цикл с параметром. вход
выход 6. Для структур итерационных циклов можно использовать символ решение (условный символ). Цикл с предусловием вход
Цикл с постусловиемвход
7. Предопределенный процесс: символ обращения к подпрограмме используется для обращения к вспомогательному алгоритму, который является таковым по отношению к основному алгоритму.
8. Данные: символ отображает данные, носитель которых не определен; можно использовать для обозначения ввода/вывода данных.
9. Соединитель: символ прерывания блок-схемы используется как указание связи между прерванными линиями потока, связывающими символы; соответствующие символы-соединители должны содержать одно и то же уникальное обозначение.
II. Контрольные вопросы. 1. Что такое алгоритм? 2. Перечислить базовые структуры алгоритмов. 3. Определить, что представляют собой цепочка и ветвление. 4. Что такое цикл как базовая структура алгоритма? 5. Какие существуют виды циклов?
III. Практическая часть. 1. Выполнение общего задания. Разобрать представленные примеры алгоритмизации задач.
Линейный алгоритм Задача 1. Постановка задачи: разработать алгоритм вычисления значения a по формуле:
Значения x, y ввести с клавиатуры; полученное значение a вывести на экран. 2. Математическая модель (метод разработки алгоритма) и описательный алгоритм задачи: • a существует при любых значения x, y, поэтому алгоритм представляется линейной структурой; • ввести значения x, y; • вычислить значение a по заданной формуле; • вывести полученное значение a. 3. Блок-схема алгоритма задачи:
Разветвленный алгоритм Задача 1 1. Постановка задачи: разработать алгоритм вычисления и вывода значения функции
y = x2+2∙x, если x≥ π/2; cos x+0,2, если 0≤x<π/2; при введенном с клавиатуры значении x. 2. Математическая модель и описательный алгоритм задачи: • так как формула вычисления y зависит от введенного значения x, то алгоритм представляется альтернативной структурой; • ввести значение x; • если x<0, то y=x3–1,5; • иначе, если x≥ π/2, то y=x2+2∙x; • иначе, если 0≤x<π/2, т.е. во всех других случаях, y=cos x+0,2; • вывести значение y. 3. Блок-схема алгоритма задачи:
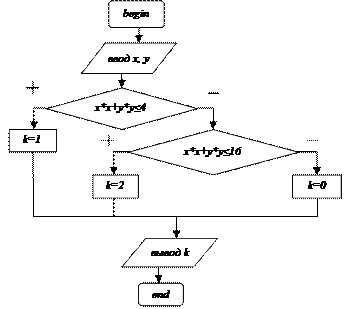
Задача 2 1. Постановка задачи: даны две окружности с центрами в начале координат и радиусами, равными 2 и 4; ввести координаты точки и определить, в окружность какого радиуса она попадает (считать, если точка попадает в меньшую окружность, то она не принадлежит большей); вывести номер окружности. 2. Математическая модель и описательный алгоритм задачи: • ввести координаты точки – x и y; • уравнение окружности: x2+y2=r2, где r – радиус окружности; • пусть условие попадания в окружность определяется значением k, тогда, если x2+y2≤4, то значение к=1, т.е. точка попадает в первую окружность; • иначе, если x2+y2≤16, то к=2, т.е. точка попадает во вторую окружность; • иначе, попадания в окружности нет, и к=0; • вывести значение k. 3. Блок-схема алгоритма задачи:
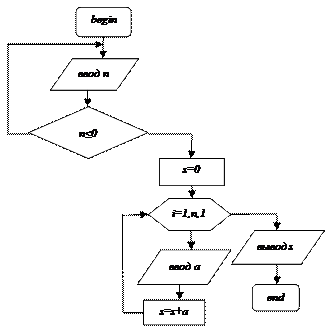
Циклические алгоритмы Задача 1 1. Постановка задачи: разработать алгоритм суммирования n введенных чисел и вывода значения суммы. 2. Математическая модель и описательный алгоритм задачи: • используя цикл с постусловием n≤0 (количество введенных чисел не может быть меньше или равно нуля), ввести количество вводимых чисел, чтобы n>0;
• для формирования суммы значение s обнулить (s=0); • в цикле c параметром i от 0 до n (количество повторений = n) каждый раз вводить значение a и формировать сумму: s=s+a; • после выхода из цикла вывести значение переменной s. 3. Блок-схема алгоритма задачи:
Задача 2 1. Постановка задачи: разработать алгоритм вычисления суммы и произведения только положительных чисел из n введенных; вывести значения суммы и произведения. 2. Математическая модель и описательный алгоритм задачи: • используя цикл с постусловием n≤0, ввести количество вводимых чисел, чтобы n>0; • для формирования суммы начальное значение s=0; • для формирования произведения начальное значение p=1; • в цикле c параметром i от 0 до n каждый раз вводить значение a и проверять: если a>0, то формировать сумму s=s+a и произведение p=p∙a; • после выхода из цикла вывести значения s и p. 3. Блок-схема алгоритма задачи:
Задача 3 1. Постановка задачи: разработать алгоритм вычисления суммы членов ряда: 2. Математическая модель и описательный алгоритм задачи: • ввести значение x; • проверить условие: если 0<x≤4, то продолжить выполнение алгоритма, иначе, выйти из алгоритма; • для формирования суммы значение S=0; • для формирования степени x начальное значение xs=x; • в цикле c параметром i от 0 до n каждый раз S увеличивается на xs, т.е S=S+xs, а xs увеличиваться в x раз, чтобы получить степень x, т.е. xs=xs∙x; • после выхода из цикла вывести значение S. 3. Блок-схема алгоритма задачи:
Задача 4 1. Постановка задачи: разработать алгоритм вычисления частичной суммы членов ряда 2. Математическая модель и описательный алгоритм задачи: • используя итерационный цикл с предусловием x≤π/3 или x>π, ввести значение, чтобы π/3<x≤π; для входа в цикл x=0, так как 0 не входит в заданный диапазон значений x; • для формирования суммы значение S=0; • начальное значение коэффициента при x: k=1; • используя цикл c предусловием для вычисления суммы членов ряда, пока очередной член ряда |cos(k∙x)/k|>ε, формировать сумму членов ряда S=S+cos(k∙x)/k и коэффициент k увеличивать на единицу для следующей итерации; • по окончанию цикла вывести значение S и количество итераций k-1 (сколько раз повторился цикл, т.е. сколько членов ряда просуммировалось, чтобы получить частичную сумму для заданного условия). 3. Блок-схема алгоритма задачи:
2. Выполнение индивидуального задания.
IV. Требования к защите индивидуальных заданий. ИМЕТЬ отчет, который включает: 1. постановку задачи; 2. математическую модель и описательный алгоритм задачи; 3. блок-схему алгоритма. ЗНАТЬ ответы на контрольные вопросы. V. Варианты индивидуальных заданий. Вариант №1 Разработать алгоритм суммирования n введенных чисел, вычисления их среднего арифметического значения и вывода полученных значений. Вариант №2 Разработать алгоритм суммирования положительных из n введенных чисел и вывода полученного значения суммы. Вариант №3 Разработать алгоритм вычисления значения функции
y = 2∙x, если x>π/4; cos x+sin x в других случаях; и вывода полученного значения.
Вариант №4 Разработать алгоритм вычисления суммы членов ряда S=x+2∙x+3∙x+…+ (n-1)ּx+nּx для -10<x<10, n=10 и вывода ее значения. Вариант №5 Разработать алгоритм суммирования и произведения n введенных чисел и вывода полученных значений суммы и произведения. Вариант №6 Разработать алгоритм суммирования только отрицательных из n введенных чисел и вывода полученного значения. Вариант №7 Разработать алгоритм суммирования n введенных чисел, вычисления среднего арифметического значения только отрицательных из этих чисел и вывода полученных значений. Вариант №8 Разработать алгоритм вычисления суммы членов ряда S=x+2∙x2+3∙x3+…+(n-1) ּ xn-1+n ּ xn для -1<x<3, n=7 и вывода полученного значения. Вариант №9 Разработать алгоритм суммирования положительных, кратных 3-м, из n введенных чисел и вывода полученного значения. Вариант №10 Разработать алгоритм вычисления произведения положительных из n введенных чисел и вывода полученного значения. Вариант №11 Разработать алгоритм вычисления среднего арифметического значения положительных из n введенных чисел и вывода полученного значения. Вариант №12 Разработать алгоритм задачи: ввести три числа, найти и вывести значение наибольшего из них. Вариант №13 Разработать алгоритм задачи: ввести три положительных числа, найти и вывести значение наименьшего из них. Вариант №14 Разработать алгоритм вычисления значения функции
y = 2∙x+5, если x>10 x в других случаях и вывода этого значения. Вариант №15 Разработать алгоритм подсчета отдельно положительных, отдельно отрицательных из n введенных чисел и вывода этих значений. Вариант №16
2∙x2+3∙x, если x<-2 y = 2∙x+7, если x≥0 -4 в других случаях и вывода этого значения. Вариант №17 Разработать алгоритм вычисления суммы членов ряда S=x+2ּ(x+1)+3ּ(x+2)+…+(n-1)ּ(x+n-2)+nּ(x+n-1) для -2<x≤4, n=8 и вывода полученного значения. Вариант №18 Разработать алгоритм суммирования отдельно отрицательных, отдельно положительных из n введенных чисел и вывода полученных значений. Вариант №19 Разработать алгоритм вычисления произведения только отрицательных из n введенных чисел с вычетом из него значения первого введенного числа и вывода полученного значения. Вариант №20 Разработать алгоритм вычисления значения функции
y = 2∙x-10, если x>10 3∙x, если -2<x≤10 и вывода этого значения. Вариант №21 Разработать алгоритм вычисления значения функции
y = 5∙x-1, если x>5 x, если 0<x≤5 и вывода этого значения. Вариант №22 Разработать алгоритм вычисления произведения только отрицательных четных чисел из n введенных и вывода полученного значения. Вариант №23* Разработать алгоритм вычисления частичной суммы членов ряда Вариант №24* Разработать алгоритм вычисления частичной суммы членов ряда S=cos(x)+cos(2ּx)+cos(3ּx)+…+cos(nּx) +… c точностью ε =10-4 для π/6<x≤π/3 и вывода ее значения. Вариант №25* Разработать алгоритм вычисления частичной суммы членов ряда Лабораторная работа № 5 Тема Обработка данных, применение стандартных и логических функций в электронных таблицах Microsoft EXCEL Цель: получить навыки ввода текстовых и числовых данных, вычисления по формулам, использования стандартных функций для вычислений, применения логических функций в электронных таблицах MS EXCEL. I. Теоретические сведения. Электронными таблицами называется класс программ, используемых для отображения и обработки данных, представленных в электронном виде.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1297; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.169.46 (0.012 с.) |



 0 (нет)
0 (нет) 4. Граница цикла: символ, отображающий начало и конец цикла; условие завершения цикла помещается внутри символа в начале или в конце в зависимости от расположения операции, проверяющей условие.
4. Граница цикла: символ, отображающий начало и конец цикла; условие завершения цикла помещается внутри символа в начале или в конце в зависимости от расположения операции, проверяющей условие.

 вход
вход 
 условие
условие


 имя
имя




 имя цикла
имя цикла

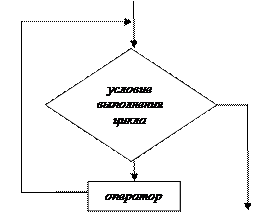 выход
выход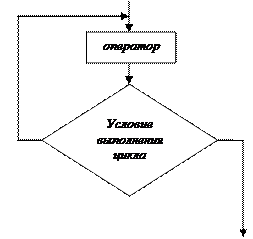 выход
выход




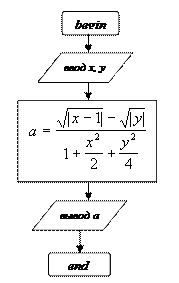
 x3–1,5, если x<0;
x3–1,5, если x<0;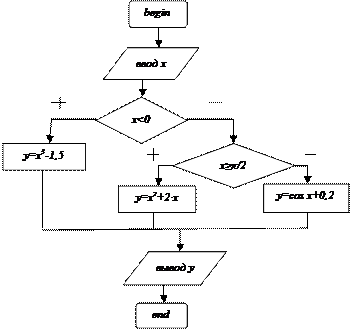


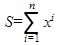 = x+x2+x3+…+xn-1+xn для 0<x≤4, n=7.
= x+x2+x3+…+xn-1+xn для 0<x≤4, n=7.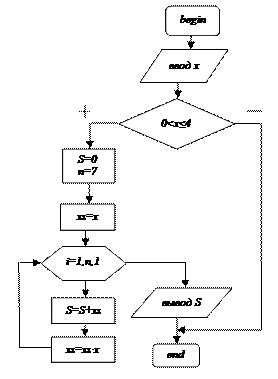
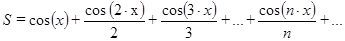 для π/3<x≤π с точностью ε =10-4, т.е. суммирование продолжать, пока очередной член ряда по модулю не будет ≤10-4.
для π/3<x≤π с точностью ε =10-4, т.е. суммирование продолжать, пока очередной член ряда по модулю не будет ≤10-4.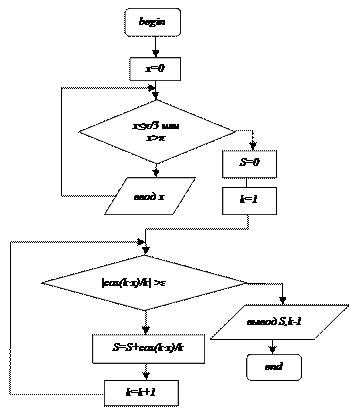
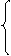 x2+1, если x≤0;
x2+1, если x≤0;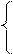 x2+3∙x, если x<-1
x2+3∙x, если x<-1 Разработать алгоритм вычисления значения функции
Разработать алгоритм вычисления значения функции x4-4∙x, если x≤-2
x4-4∙x, если x≤-2 x2-4∙x-1, если x≤0
x2-4∙x-1, если x≤0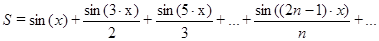 с точностью ε=10-5 для π/4<x≤2π и вывода ее значения.
с точностью ε=10-5 для π/4<x≤2π и вывода ее значения.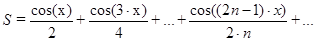 с точностью ε=10-3 для π/6<x≤π и вывода ее значения.
с точностью ε=10-3 для π/6<x≤π и вывода ее значения.


