
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 17. О расширении множества натуральных чиселСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Содержание 1. Понятие дроби. 2. Положительные рациональные числа. 3. Запись положительных рациональных чисел в виде десятичных дробей. 4. Действительные числа. Основная литература [1, 2, 6, 7, 9-13, 17, 18, 23, 33, 34]; Дополнительная литература [31, 43, 55] Введение. Большинство применений математики связано с измерением величин. Однако для этих целей натуральных чисел недостаточно: не всегда единица величины укладывается целое число раз в измеряемой величине. Чтобы в такой ситуации точно выразить результат измерения, необходимо расширить запас чисел, введя числа, отличные от натуральных. К этому выводу люди пришли еще в глубокой древности: измерение длин, площадей, масс и других величин привело сначала к возникновению дробных чисел - получили рациональные числа, а в V в до н.э. математиками школы Пифагора было установлено, что существуют отрезки, длину которых при выбранной единице длины нельзя выразить рациональным числом. Позднее, в связи с решением этой проблемы, появились числа иррациональные. Рациональные и иррациональные числа назвали действительными. Строгое определение действительного числа и обоснование его свойств было дано в XIX в. Действительные числа - не последние в ряду различных чисел. Процесс, начавшийся с расширения множества натуральных чисел, продолжается и сегодня - этого требует развитие различных наук и самой математики. Знакомство учащихся с дробными числами происходит, как правило, в начальных классах. Затем понятие дроби уточняется и расширяется в средней школе. В связи с этим учителю необходимо владеть понятием дроби и рационального числа, знать правила выполнения действий над рациональными числами, свойства этих действий. Все это нужно не только для того, чтобы математически грамотно ввести понятие дроби и обучать младших школьников выполнять с ними действия, но и, что не менее важно, видеть взаимосвязи множеств рациональных и действительных чисел с множеством натуральных чисел. Без их понимания нельзя решить проблему преемственности в обучении математике в начальных и последующих классах школы. Расширение множества N натуральных чисел будет происходить в такой последовательности: сначала строится множество Q+ положительных рациональных чисел, затем показывается, как его можно расширить до множества R+ положительных действительных чисел, и, наконец, очень кратко описывается расширение множества R+ до множества R всех действительных чисел. Понятие дроби
И тогда, говоря о длине отрезка х, мы должны указать два числа 4 и 14: четвертая часть отрезка е укладывается в отрезке точно 14 раз. Поэтому условились длину отрезка х записывать в виде Определение. Пусть даны отрезок х и единичный отрезок е, длина которого Е. Если отрезок х состоит из т отрезков, равных п-ой части отрезка е, то длина отрезка х может быть представлена в виде В записи дроби Дробь Вернемся к рисунку 1, где показано, что четвертая часть отрезка е уложилась в отрезке х точно 14 раз. Очевидно, это не единственный вариант выбора такой части отрезка е, которая укладывается в отрезке х целое число раз. Можно взять восьмую часть отрезка е, тогда отрезок х будет состоять из 28 таких частей и его длина будет выражаться дробью Вообще длина одного и того же отрезка х при заданном единичном отрезке е может выражаться различными дробями, причем, если длина выражена дробью Теорема. Для того чтобы дроби Доказательство этой теоремымы опускаем. Определение. Две дроби Если дроби равны, то пишут Например, Из сформулированных выше теоремы и определения следует, что две дроби равны тогда и только тогда, когда они выражают длину одного и того же отрезка. Нам известно, что отношение равенства дробей рефлексивно, симметрично и транзитивно, т.е. является отношением эквивалентности. Теперь, используя определение равных дробей, это можно доказать. Теорема.Равенство дробей является отношением эквивалентности. Доказательство. Действительно, равенство дробей рефлексив но: Равенство дробей симметрично: если Из определения равных дробей вытекает основное свойство дроби. Напомним его. Основное свойство дроби. Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится дробь, равная данной. На этом свойстве основано сокращение дробей и приведение дробей к общему знаменателю. Сокращение дробей - это замена данной дроби другой, равной данной, но с меньшим числителем и знаменателем. Если числитель и знаменатель дроби одновременно делятся только на единицу,то дробь называют несократимой. Например, Приведение дробей к общему знаменателю - это замена данных дробей равными им дробями, имеющими одинаковые знаменатели. Общим знаменателем двух дробей Например. Привести к наименьшему общему знаменателю дроби Решение. Разложим числа 15 и 35 на простые множители: 15=3×5, 35=5×7. Тогда К(15,35)=3×5×7=105. Поскольку 105=15×7=35 ×3, то
|
|||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 788; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.46.108 (0.007 с.) |

 Е где Е- длина единичного отрезка е, а символ
Е где Е- длина единичного отрезка е, а символ  называть дробью.
называть дробью. Е, где символ — называют дробью (и читают «эм энных»).
Е, где символ — называют дробью (и читают «эм энных»). числа m и n - натуральные, m называется числителем, n - знаменателем дроби.
числа m и n - натуральные, m называется числителем, n - знаменателем дроби. называется правильной, если ее числитель меньше знаменателя, и неправильной, если ее числитель больше знаменателяилиравен ему.
называется правильной, если ее числитель меньше знаменателя, и неправильной, если ее числитель больше знаменателяилиравен ему. . Можно взять шестнадцатую часть отрезка е, тогда отрезок х будет состоять из 56 таких частей и его длина будет выражаться дробью
. Можно взять шестнадцатую часть отрезка е, тогда отрезок х будет состоять из 56 таких частей и его длина будет выражаться дробью 
 , то она может быть выражена и любой дробью вида
, то она может быть выражена и любой дробью вида 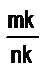 , где k-натуральное число.
, где k-натуральное число. и
и  выражали длину одного того же отрезка, необходимо и достаточно, чтобы выполнялось равенство тq = пр.
выражали длину одного того же отрезка, необходимо и достаточно, чтобы выполнялось равенство тq = пр. и
и  называются равными, если т q = пр.
называются равными, если т q = пр.
 , таккак 17×21 = 119×3, а
, таккак 17×21 = 119×3, а  потому что 17×27=459, 19×23 = 437 и 459 ¹ 437.
потому что 17×27=459, 19×23 = 437 и 459 ¹ 437. =
=  ,так как равенство mn = nm справедливо для любых натуральных чисел n и m.
,так как равенство mn = nm справедливо для любых натуральных чисел n и m.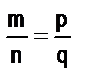 , то
, то  , так как из mq = nр следует, что рn = qm (m, n, р, qÎN). Оно транзитивно: если
, так как из mq = nр следует, что рn = qm (m, n, р, qÎN). Оно транзитивно: если  и
и  , то
, то  . В самом деле, так как
. В самом деле, так как  , то mq = nр, а так как
, то mq = nр, а так как  , то рs = qr. Умножив обе части равенства mq = nр на s, а равенства рs = qr на n, получим mqs = nрs и nрs = qrs. Откуда mqs =qrn или ms = nr. Последнее равенство означает, что
, то рs = qr. Умножив обе части равенства mq = nр на s, а равенства рs = qr на n, получим mqs = nрs и nрs = qrs. Откуда mqs =qrn или ms = nr. Последнее равенство означает, что  . Итак, равенство дробей рефлексивно, симметрично и транзитивно, следовательно, оно является отношением эквивалентности.
. Итак, равенство дробей рефлексивно, симметрично и транзитивно, следовательно, оно является отношением эквивалентности. - несократимая дробь, так как ее числитель и знаменатель делятся одновременно только на единицу.
- несократимая дробь, так как ее числитель и знаменатель делятся одновременно только на единицу. и
и  является общее кратное чисел n и q, а наименьшим общим знаменателем - их наименьшее кратное К(n, q).
является общее кратное чисел n и q, а наименьшим общим знаменателем - их наименьшее кратное К(n, q). и
и 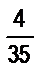 .
. ,
, 



