
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прямая и обратная пропорциональностиСодержание книги
Поиск на нашем сайте
Если t - время движения пешехода (в часах), s - пройденный путь (километрах), и он движется равномерно со скоростью 4 км/ч, то зависимость между этими величинами можно выразить формулой s = 4t Так как каждому значению t соответствует единственное значение, то можно говорить о том, что с помощью формулы s = 4t задан функция. Ее называют прямой пропорциональностью и определяю следующим образом. Определение. Прямой пропорциональностью называется функции которая может быть задана при помощи формулы у = kx, где k не равное нулю действительное число. Название функции у = k х связано с тем, что в формуле у = k х есть переменные х и у, которые могут быть значениями величин. А если отношение двух величин равно некоторому числу, отличному от нуля, их называют прямо пропорциональными. В нашем случае Это число называют коэффициентом пропорциональности. Функция у = k х является математической моделью многих реальных ситуаций, рассматриваемых уже в начальном курсе математики. Одна из них описана выше. Другой пример: если в одном пакете муки 2 кг, а куплено х таких пакетов, то всю массу купленной муки (обозначим ее через у) можно представить в виде формулы у = 2х, т. е. зависимость между количеством пакетов и всей массой купленной муки является прямой пропорциональностью с коэффициентом k = 2. Напомним некоторые свойства прямой пропорциональности, которые изучаются в школьном курсе математики. 1. Областью определения функции у = k х и областью ее значений является множество действительных чисел. 2. Графиком прямой пропорциональности является прямая, проходящая через начало координат. Поэтому для построения графика прямой пропорциональности достаточно найти лишь одну точку, принадлежащую ему и не совпадающую с началом координат, а затем через эту точку и начало координат провести прямую.
Например, чтобы построить график функции у = k х, достаточно иметь точку с координатами (1,2), а затем через нее и начало координат провести прямую (рис. 7). 3. При k > 0 функция у = kх возрастает на всей области определения, при k < 0 — убывает на всей области определения.
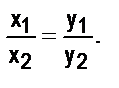 Действительно, если функция f - прямая пропорциональность, то она может быть задана формулой у = kх, и тогда у1 = kх1, у2 = kх2. Так как х2 ¹ 0 и k¹0, то у2¹0. Поэтому Замечание. Если значениями переменных х и у служат положительные действительные целые числа, то доказанное свойство прямой пропорциональности можно сформулировать так: с увеличением (уменьшением) значения переменной х в несколько раз соответствующее значение переменной у увеличивается (уменьшается) во столько же раз. Это свойство присуще только прямой пропорциональности, и им можно пользоваться при решении текстовых задач, в которых рассматриваются прямо пропорциональные величины. Задача 1. За 8 ч токарь изготовил 16 деталей. Сколько часов потребуется токарю на изготовление 48 деталей, если он будет работать с той же производительностью? Решение. В задаче рассматриваются величины - время работы токаря, количество сделанных им деталей и производительность (т.е. количество деталей, изготавливаемых токарем за 1 ч), причем последняя величина постоянна, а две другие принимают различные значения. Кроме того, количество сделанных деталей и время работы - величины прямо пропорциональные, так как их отношение равно некоторому числу, не равному нулю, а именно - числу деталей, изготавливаемых токарем за 1 ч. Если количество сделанных деталей обозначит буквой у, время работы х, а производительность – k, то получим, что Решить задачу можно двумя арифметическими способами: 1 способ: 2 способ: 1) 16:8 =2 (дет.) 1) 48:16 = 3 (раза) 2) 48:2=24(ч) 2) 8×3=24(ч) Решая задачу первым способом, мы сначала нашли коэффициент пропорциональности k, он равен 2, а затем, зная, что у = 2х, нашли значение х при условии, что у = 48. При решении задачи вторым способом мы воспользовались свойством прямой пропорциональности: во сколько раз увеличивается количество деталей, сделанных токарем, во столько же раз увеличивается и количество времени на их изготовление. Перейдем теперь к рассмотрению функции, называемой обратной пропорциональностью. Если t - время движения пешехода (в часах), v - его скорость (в км/ч) и он прошел 12 км, то зависимость между этими величинами можно выразить формулой v × t = 20 или v = Определение. Обратной пропорциональностью называется функция, которая может быть задана при помощи формулы Название данной функции связано с тем, что в Функция Одна из них описана перед определением обратной пропорциональности. Другой пример: если купили 12 кг муки и разложили ее в х пакетов по у кг в каждую, то зависимость между данными величинами можно представить в виде х×у = 12, т.е. она является обратной пропорциональностью с коэффициентом k = 12. Напомним некоторые свойства обратной пропорциональности, известные из школьного курса математики. 1. Областью определения функции 2. Графиком обратной пропорциональности является гипербола. 3. При k > 0 ветви гиперболы расположены в 1-й и 3-й четвертях и функция у у k > 0 k < 0 х х
Рис. 8 Рис. 9 4. Если функция f – обратная пропорциональность и (х1, у1), (х2, у2) – пары соответствующих значений переменных х и у, то Действительно, если функция f - обратная пропорциональность, она может быть задана формулой Замечание. Если значениями переменных х и у служат положительные действительные числа, то это свойство обратной пропорциональности можно сформулировать так: с увеличением (уменьшением) значения переменной х в несколько раз соответствующее значение переменной у уменьшается (увеличивается) во столько же раз. Это свойство присуще только обратной пропорциональности, и им можно пользоваться при решении текстовых задач, в которых рассматриваются обратно пропорциональные величины. Задача 2. Велосипедист, двигаясь со скоростью 10 км/ч, проехал расстояние от А до В за 6 ч. Сколько времени потратит велосипедист на обратный путь, если будет ехать со скоростью 20 км/ч? Решение. В задаче рассматриваются величины: скорость движения велосипедиста, время движения и расстояние от А до В, причем последняя величина постоянна, а две другие принимают различные значения. Кроме того, скорость и время движения - величины обратно пропорциональные, так как их произведение равно некоторому числу, а именно пройденному расстоянию. Если время движения велосипедиста обозначить буквой у, скорость - х, а расстояние АВ - k, то получим, что ху = k или Решить задачу можно двумя способами: 1 способ: 2 способ: 1) 10×6 =60 (км) 1) 20:10=2 (раза) 2) 60:20=3(ч) 2) 6:2=3(ч) Решая задачу первым способом, мы сначала нашли коэффициент пропорциональности k, он равен 60, а затем, зная, что При решении задачи вторым способом мы воспользовались свойством обратной пропорциональности: во сколько раз увеличивается скорость движения, во столько же раз уменьшается время на прохождение одного и того же расстояния. Замечание. При решении конкретных задач с обратно пропорциональными или прямо пропорциональными величинами накладываются некоторые ограничения на х и у, в частности, они могут рассматриваться не на всем множестве действительных чисел, а на его подмножествах. Задача 3. Лена купила х карандашей, а Катя в 2 раза больше. Обозначьте число карандашей, купленных Катей, через у, выразите у через х и постройте график установленного соответствия при условии, что х£5. Является ли это соответствие функцией? Какова ее область определения и область значений? Решение. Катя купила у=2х карандашей. При построении графика функции у=2х необходимо учесть, что переменная х - обозначает количество карандашей и х£5, значит, она может принимать только значения 0, 1, 2, 3, 4, 5. Это и будет область определения данной функции. Чтобы получить область значений данной функции, надо каждое значение х из области определения умножить на 2, т.е. это будет множество {0, 2, 4, 6, 8, 10}. ПРАКТИЧЕСКАЯ РАБОТА. ФУНКЦИЯ И ЕЕ СВОЙСТВА Цель. Раскрыть теоретические основы формирования функциональной зависимости в курсе начальной математики. Теоретическая часть 1. Исторические сведения о возникновении понятия функции. 2. Понятие функции. Способы задания функции. 3. Прямая пропорциональность. 4. Обратная пропорциональность. Основные понятия темы Ø числовая функция; Ø область определения функции; Ø область значений функции; Ø график функции; Ø прямая пропорциональность; Ø обратная пропорциональность. Основные выводы, замечания Ø Числовую функцию можно задать с помощью формулы (она представляет собой уравнение с двумя переменными), графика на координатной плоскости, таблицы. Ø Функции могут обладать свойством монотонности, т.е. возрастать или убывать на некотором промежутке. Ø Свойства, присущие только прямой и обратной пропорциональности можно использовать при обучении младших школьников решению задач с пропорциональными величинами. Практическая часть Обязательные задания 1. Понятие функции является фундаментальным математическим понятием. В процессе эволюции математики оно определенным образом изменилось. Раскройте основные этапы возникновения определения функции в историческом аспекте. Приведите примеры пропедевтических учений Н. Орема (1323-1382), Г.В. Лейбница (1646-1716), И. Бернулли (1718г.), Л.Эйлера (1707-1783) о функции. Дайте определение функции М.И. Лобачевским (19 в.) и определения функции в современных учебниках алгебры и математики. 2. Каждому целому неотрицательному числу поставлен в соответствие его остаток от деления на 5. Изобразите схематично это соответствие, взяв в качестве множества X первые 20 натуральных чисел. Будет ли это соответствие функцией? Каким числам соответствует нуль? 3. Соответствие f задано следующим образом: «Каждому двузначному числу соответствует сумма его цифр». Убедитесь, что это соответствие является функцией. Укажите область определения и множество значений функции. Вычислите значения функции f (41); f (56); f (83). При каких значениях аргумента значение функции равно 2? 4. Представьте различными способами число 5 как сумму двух натуральных чисел. Запишите аналитически связь между слагаемыми. Сколькими способами можно представить 5 как сумму двух натуральных чисел? 5. Какие из следующих формул задают на множестве R действительных чисел функцию: а) у = 4х; б) 6. Связь между переменными х и у задана формулой х2 + у2 = 25. Задайте эту связь словесно и геометрически. Выразите каждую из переменных через другую. Являются ли эти зависимости функциями? Если нет, то измените соответствующие формулы так, чтобы они задавали функции. 7. Постройте график функции у = 5 - х, если ее область определения такова: а) Х = {0,1, 2, 3,4, 5}; б) Х = [0;5]; в) Х = R. 8. Постройте графики следующих функций при условии, что они заданы на множестве R действительных чисел: а) у = х; б) у = 3; в) х = 5; г) у = 0. 9. Функция f задана при помощи таблицы:
а) Укажите ее область определения и область значений. б) Задайте функцию f при помощи формулы. в) Постройте график функции f на координатной плоскости. г) Докажите, что функция f возрастает на всей области определения. 10. Докажите, что соответствие между значениями переменных х и у, рассматриваемое в задаче, является функцией; укажите область ее значений при условии, что х < 5; постройте график данной функции: а) Катя купила 3 тетради, а Лена на х тетрадей больше. Сколько тетрадей (у) купили Лена и Катя вместе? б) Из пунктов А и В навстречу друг другу вышли два туриста. При встрече оказалось, что один прошел 3 км, а второй на х км больше. Каково расстояние (у км) между пунктами А и В? 11. Сравните функции, о которых идет речь в предыдущем упражнении. Чем они похожи? В чем их различие? Какими будут графики данных функций? 12. У одного ученика было 2 тетради. В течение 6 дней он каждый день покупал по 3 новых тетради. Сколько тетрадей (у) у него будет через х дней? Выразите у через х и покажите, что установленное соответствие - функция. Укажите ее область определения и область значений. Постройте график. 13. Известно, что функция f является прямой пропорциональностью, задана на множестве Х = {1, 2, 3, 4, 5, 6} и при х, равном 3, значение функции равно 12. а) Задайте функцию f при помощи формулы и таблицы; постройте ее график. б) Какие свойства функции f можно проиллюстрировать при помощи таблицы и графика? в) Какие из названных свойств вы будете использовать, решая задачу: «В 3 пакета разложили поровну 12 кг муки. Сколько килограммов муки можно разложить в 6 таких пакетов?» 14. Известно, что функция f является обратной пропорциональностью, задана на множестве Х = {1,2, 3, 5, 6, 10, 15, 30} и при х, равном 5, значение функции f равно 6. а) Задайте функцию f при помощи формулы и таблицы; постройте ее график. б) Какие свойства функции f можно проиллюстрировать при помощи таблицы и графика? в) Какие из названных свойств вы будете использовать, решая задачу: «Муку разложили в 10 пакетов по 3 кг в каждый. Сколько получилось бы пакетов, если бы в каждый положили по 6 кг муки?» 15. Покажите, что зависимость между величинами, о которых идет речь в нижеприведенной задаче, может быть выражена формулой у = kх. Из 24 м ткани сшили 8 одинаковых платьев. Сколько потребуется ткани на 16 таких же платьев? 16. Учитель, проводя с детьми анализ задачи (см. пред. упр.), спрашивает: «Если на 8 платьев израсходовали 24 м ткани, то на 16 платьев израсходуют больше или меньше ткани?» Дети отвечают, что больше, так как 16 больше 8. О каком свойстве и какой функции в этом случае идет речь? 17. Задайте при помощи формулы соответствие, которое рассматривается в задании: а) Запиши несколько примеров на деление с результатом 10. б) Составь все возможные примеры на сложение однозначных чисел с ответом 10. Установите, являются ли эти соответствия функциями. 18. Одна сторона прямоугольника 3 см, а другая - х см. Какова площадь (у см2) этого прямоугольника? Постройте график полученного соответствия при условии, что х £ 6. Докажите, что это соответствие - функция. 19. Площадь прямоугольника с основанием х см равна 12 см2. Какова высота (у см) этого прямоугольника? Покажите, что соответствие между значениями переменных х и у является функцией и постройте ее график при условии, что 1 £ х £ 12. 20. Какие из нижеприведенных задач можно решить в начальной школе двумя способами: а) Велосипедист ехал со скоростью 12 км/ч и был в пути 2 ч. Сколько времени потребуется пешеходу, чтобы пройти это расстояние со скоростью 4 км/ч? б) Из 100 кг свеклы при переработке получается 16 кг сахара. Сколько килограммов сахара получится из 3 т свеклы? в) Два опытных участка имеют одинаковую площадь. Ширина первого участка 30 м, ширина второго - 40 м. Найдите длину первого участка, если известно, что длина второго участка равна 75 м. Творческие задания 1. Составьте текстовую задачу, которую можно было бы решить в начальном курсе математики, на зависимость вида: у = 4х. Является ли данное уравнение моделью этой задачи? 2. Составьте текстовую задачу, которую можно было бы решить в начальном курсе математики, на зависимость вида: у = 60х. 3. Найдите учебника математики для начальной школы текстовые задачи на зависимость вида у = кх. 4. Составьте текстовую задачу, которую можно было бы решить в начальном курсе математики, на зависимость вида: у = 4х + 2. 5. Составьте текстовую задачу, которую можно было бы решить в начальном курсе математики, на зависимость вида: у = 15х + 20. 6. Составьте текстовую задачу на зависимость вида у = х/6. 7. Составьте текстовую задачу на зависимость вида у = х/4. 8. Приведите примеры текстовых задач начального курса математики, между величинами которых прямая пропорциональная зависимость.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 2174; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.231.116 (0.009 с.) |

 .
.
 и значит
и значит 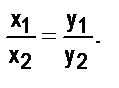
 или у = k х, т.е. математической моделью ситуации, представленной в задаче, является прямая пропорциональность.
или у = k х, т.е. математической моделью ситуации, представленной в задаче, является прямая пропорциональность. . Так как каждому значению t (t¹0) соответствует единственное значение скорости v, то можно говорить о том, что с помощью формулы v =
. Так как каждому значению t (t¹0) соответствует единственное значение скорости v, то можно говорить о том, что с помощью формулы v =  . задана функция. Ее называют обратной пропорциональностью и определяют следующим образом.
. задана функция. Ее называют обратной пропорциональностью и определяют следующим образом. есть переменные х и у, которые могут быть значениями величин. А если произведение двух величин равно некоторому числу, отличному от нуля, то их называют обратно пропорциональными. В нашем случае ху = k (k ¹ 0). Это число k называют коэффициентом пропорциональности.
есть переменные х и у, которые могут быть значениями величин. А если произведение двух величин равно некоторому числу, отличному от нуля, то их называют обратно пропорциональными. В нашем случае ху = k (k ¹ 0). Это число k называют коэффициентом пропорциональности. является математической моделью многих реальных ситуации, рассматриваемых уже в начальном курсе математики.
является математической моделью многих реальных ситуации, рассматриваемых уже в начальном курсе математики. областью ее значений х является множество действительных чисел, отличных от нуля.
областью ее значений х является множество действительных чисел, отличных от нуля. является убывающей на всей области определения х (рис.8). При k < 0 ветви гиперболы расположены во 2-й и 4-й четверти функция
является убывающей на всей области определения х (рис.8). При k < 0 ветви гиперболы расположены во 2-й и 4-й четверти функция  является возрастающей на всей области определения х (рис. 9).
является возрастающей на всей области определения х (рис. 9).
 ,
,  . Так как х1¹0, х2¹0, то
. Так как х1¹0, х2¹0, то  .
. нашли значение у при условии, что х = 20.
нашли значение у при условии, что х = 20. у =; в) х2 + у2 = 4?
у =; в) х2 + у2 = 4?


