Числовые функции можно представлять наглядно на координатной плоскости.

Пусть у = f (х) функция с областью определения X. Тогда ее графиком является множество таких точек координатной плоскости, которые имеют абсциссу х и ординату f (х) для всех х из множества X.

Так, графиком функции у = 2х - 3, заданной на множествеR, является прямая (рис.1), а графиком функции у = х², заданной также на множествеR, - парабола (рис. 2).

 

Р

Рис. 1 Рис.2

Функции можно задавать при помощи графика.

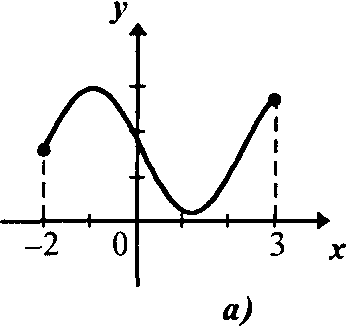
Например, графики, приведенные на рисунке 3, задают функции, одна из которых имеет в качестве области определения промежуток [-2, З], а вторая - конечное множество {-1, 0, 1, 2, 3}.

у

 

 

·

· · · ·

-1 3 х

б)

Рис. 3

Не каждое множество точек на координатной плоскости представ­ит собой график некоторой функции. Так как при каждом значении аргумента из области определения функция должна иметь лишь одно значение, то любая прямая, параллельная оси ординат, или совсем не пересекает график функции, или пересекает его лишь в одной точке. Если же это условие не выполняется, то множество точек координат­ной плоскости график функции не задает.

Рис. 4

На­пример, кривая на рисунке 4 не является гра­фиком функции - прямая АВ, параллельная оси ординат, пересекает ее в двух точках.

Ø Функции можно задавать при помощи таблицы.

Например, таблица, приведенная ниже, описывает зависимость температуры воздуха от времени суток. Эта зависимость - функция, так как каждому значению времени f соответствует единственное значение температуры воздуха p?:

T (в часах)
P (в градусах Цельсия)

Числовые функции обладают многими свойствами. Мы рассмотрим одно из них - свойство монотонности, так как понимание этого свойства учителем важно при обучении математике младших школьников.

Определение. Функция f называется монотонной на некотором промежутке А, если она на этом промежутке возрастает или убывает.

Определение. Функция f называется возрастающей на некотором промежутке А, если для любых чисел х₁, х₂ из множества А выпол­няется условие: х₁ <х₂ Þ f (х₁) < f (х₂).

График функции, возрастающей на промежутке А, обладает особенностью: при движении вдоль оси абсцисс слева направо по про­межутку А ординаты точек графика увеличиваются (рис. 5).

Определение. Функция f называется убывающей на некотором промежутке А, если для любых чисел х₁, х₂ из множества А выполняется условие: х₁ <х₂ Þ f (х₁) > f (х₂).

График функции, убывающей на промежутке А, обладает особенностью: при движении вдоль оси абсцисс слева направо по про­межутку А ординаты точек графика уменьшаются (рис. 6).

Рис. 5 Рис.6