
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 9. Дифференциальные уравненияСодержание книги
Поиск на нашем сайте
Дифференциальные уравнения Задачи, приводящие к понятию дифференциального уравнения. Общее и частное решения. Задача Коши. Дифференциальные уравнения 1-го порядка Дифференциальные уравнения 1 порядка. Теорема о существовании и единственности решения задачи Коши. Дифференциальные уравнения с разделяющимися переменными. Однородные дифференциальные уравнения. Линейные дифференциальные уравнения 1-го порядка Линейные дифференциальные уравнения порядка. Метод подстановки и метод Лагранжа решения линейного дифференциального уравнения 1 порядка. Уравнение Бернулли. ДУ в полных дифференциалах Дифференциальные уравнения в полных дифференциалах и их решение. Интегрирующий множитель. Дифференциальные уравнения высших порядков Дифференциальные уравнения высших порядков. Линейные однородные дифференциальные уравнения Линейные однородные дифференциальные уравнения и свойства их решений. Линейные однородные дифференциальные уравнения 2 порядка с постоянными коэффициентами. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами Линейные неоднородные дифференциальные уравнения 2 порядка с постоянными коэффициентами. Метод вариации постоянной для нахождения частного решения неоднородного уравнения. Линейные неоднородные дифференциальные уравнения со специальной правой частью. Системы дифференциальных уравнений Нормальные системы дифференциальных уравнений. Метод исключения решения нормальной системы. Решение линейной однородной системы. Раздел 10. Теория вероятностей и математическая статистика Вероятность события Предмет теории вероятностей. Пространство элементарных событий. Элементы комбинаторики. Определение вероятности события. Относительная частота события. Геометрическая вероятность. Основные теоремы теории вероятностей Теоремы сложения и умножения вероятностей. Условная вероятность, формулы Бейеса. Последовательности независимых испытаний Последовательности независимых испытаний. Теоремы Муавра - Лапласа и Пуассона. Случайные величины и их числовые характеристики Закон распределения дискретной случайной вели чины. Непрерывные случайные величины. Функция распределения и ее свойства. Плотность распределения вероятностей и ее свойства. Математическое ожидание и дисперсия. Законы распределения случайных величин Примеры распределений: биномиальное распределение, распределение Пуассона, равномерное распределение, показательное распределение, нормальное распределение. Закон больших чисел. Основные понятия математической статистики Предмет и задачи математической статистики. Способы отбора и представления статистических данных. Эмпирическая функция распределения выборки. Числовые характеристики выборки. Оценка параметров распределения, проверка гипотез Точечная оценка параметров распределения, метод моментов. Интервальные оценки параметров распределения. Определение доверительного интервала для математического ожидания нормально распределенной совокупности при известной дисперсии. Распределение Применение методов математической статистике в деятельности подразделений МЧС Понятие о математическом моделировании деятельности органов и подразделений по чрезвычайным ситуациям. Определение вероятности возникновения пожара (взрыва) в пожаровзрывоопасном объекте. Определение уровня обеспечения пожаровзрывобезопасности людей.
КОНТРОЛЬНАЯ РАБОТА № 7
|
||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 176; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.158.10 (0.008 с.) |

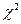 . Статистическая гипотеза. Проверка гипотезы с помощью критерия Пирсона. Линейная корреляция и регрессия.
. Статистическая гипотеза. Проверка гипотезы с помощью критерия Пирсона. Линейная корреляция и регрессия.


