
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Размерные константы в уравнениях МаксвеллаСодержание книги
Поиск на нашем сайте
В гауссовой системе единиц СГС все поля имеют одинаковую размерность, и в уравнениях Максвелла фигурирует единственная фундаментальная константа В системе единиц СИ, чтобы связать электрическую индукцию и напряжённость электрического поля в вакууме, вводится электрическая постоянная Скорость электромагнитного излучения в вакууме (скорость света) в СИ появляется при выводе волнового уравнения:
В системе единиц СИ, в качестве точных размерных констант определены скорость света в вакууме Принятые значения[34] скорости света, электрической и магнитной постоянных приведены в таблице:
Иногда вводится величина, называемая «волновым сопротивлением», или «импедансом» вакуума:
Приближённое значение для Уравнения Максвелла в среде Чтобы получить полную систему уравнений электродинамики, к системе уравнений Максвелла необходимо добавить материальные уравнения, связывающие величины Связанные заряды и токи
Слева: Совокупность микроскопических диполей в среде образуют один макроскопический дипольный момент и эквивалентны двум заряженным с противоположным знаком пластинам на границе. При этом внутри среды все заряды скомпенсированы; Справа: Совокупность микроскопических циркулярных токов в среде эквивалентна макроскопическому току, циркулирующему вдоль границы. При этом внутри среды все токи скомпенсированы. При приложении электрического поля к диэлектрическому материалу каждая из его молекул превращается в микроскопический диполь. При этом положительные ядра атомов немного смещаются в направлении поля, а электронные оболочки в противоположном направлении. Кроме этого, молекулы некоторых веществ изначально имеют дипольный момент. Дипольные молекулы стремятся ориентироваться в направлении поля. Этот эффект называется поляризацией диэлектриков. Такое смещение связанных зарядов молекул в объёме эквивалентно появлению некоторого распределения зарядов на поверхности, хотя все молекулы, вовлечённые в процесс поляризации остаются нейтральными (см. рисунок). Аналогичным образом происходит магнитная поляризация (намагничивание) в материалах, в которых составляющие их атомы и молекулы имеют магнитные моменты, связанные со спином и орбитальным моментом ядер и электронов. Угловые моменты атомов можно представить в виде циркулярных токов. На границе материала совокупность таких микроскопических токов эквивалентна макроскопическим токам, циркулирующим вдоль поверхности, несмотря на то, что движение зарядов в отдельных магнитных диполях происходит лишь в микромасштабе (связанные токи). Рассмотренные модели показывают, что хотя внешнее электромагнитное поле действует на отдельные атомы и молекулы, его поведение во многих случаях можно рассматривать упрощённым образом в макроскопическом масштабе, игнорируя детали микроскопической картины. В среде сторонние электрические и магнитные поля вызывают поляризацию и намагничивание вещества, которые макроскопически описываются соответственно вектором поляризации
Поляризация
Поэтому, выражая векторы
Индексом Материальные уравнения Материальные уравнения устанавливают связь между
где введены безразмерные константы:
где
где
Аналогичные уравнения получаются в гауссовой системе СГС (если формально положить
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 362; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.177.204 (0.007 с.) |

 , имеющая размерность скорости, которая сейчас называется скоростью света (именно равенство этой константы скорости распространения света дало Максвеллу основания для гипотезы об электромагнитной природе света[32]).
, имеющая размерность скорости, которая сейчас называется скоростью света (именно равенство этой константы скорости распространения света дало Максвеллу основания для гипотезы об электромагнитной природе света[32]). (
( ). Магнитная постоянная
). Магнитная постоянная  является таким же коэффициентом пропорциональности для магнитного поля в вакууме (
является таким же коэффициентом пропорциональности для магнитного поля в вакууме (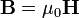 ). Названия электрическая постоянная и магнитная постоянная сейчас стандартизованы[33]. Ранее для этих величин также использовались, соответственно, названия диэлектрическая и магнитная проницаемости вакуума.
). Названия электрическая постоянная и магнитная постоянная сейчас стандартизованы[33]. Ранее для этих величин также использовались, соответственно, названия диэлектрическая и магнитная проницаемости вакуума.
 (точно)
(точно)


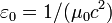

 Ом.
Ом. получается, если для скорости света принять значение
получается, если для скорости света принять значение  м/c. В системе СГС
м/c. В системе СГС  . Эта величина имеет смысл отношения амплитуд напряжённостей электрического и магнитного полей плоской электромагнитной волны в вакууме.
. Эта величина имеет смысл отношения амплитуд напряжённостей электрического и магнитного полей плоской электромагнитной волны в вакууме.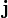 ,
, 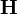 ,
, 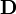 ,
, 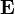 ,
, 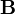 , в которых учтены индивидуальные свойства среды. Способ получения материальных уравнений дают молекулярные теории поляризации, намагниченности и электропроводности среды, использующие идеализированные модели среды. Применяя к ним уравнения классической или квантовой механики, а также методы статистической физики, можно установить связь между векторами
, в которых учтены индивидуальные свойства среды. Способ получения материальных уравнений дают молекулярные теории поляризации, намагниченности и электропроводности среды, использующие идеализированные модели среды. Применяя к ним уравнения классической или квантовой механики, а также методы статистической физики, можно установить связь между векторами 

 и вектором намагниченности
и вектором намагниченности  вещества, а вызваны появлением связанных зарядов
вещества, а вызваны появлением связанных зарядов  и токов
и токов  . В результате поле в среде оказывается суммой внешних полей и полей, вызванных связанными зарядами и токами.
. В результате поле в среде оказывается суммой внешних полей и полей, вызванных связанными зарядами и токами.




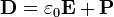



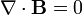
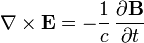
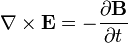


 здесь обозначены свободные заряды и токи. Уравнения Максвелла в такой форме являются фундаментальными, в том смысле, что они не зависят от модели электромагнитного устройства вещества. Разделение зарядов и токов на свободные и связанные позволяет «спрятать» в
здесь обозначены свободные заряды и токи. Уравнения Максвелла в такой форме являются фундаментальными, в том смысле, что они не зависят от модели электромагнитного устройства вещества. Разделение зарядов и токов на свободные и связанные позволяет «спрятать» в  и, следовательно, в
и, следовательно, в  сложный микроскопический характер электромагнитного поля в среде.
сложный микроскопический характер электромагнитного поля в среде. и
и 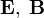 . При этом учитываются индивидуальные свойства среды. На практике в материальных уравнениях обычно используются экспериментально определяемые коэффициенты (зависящие в общем случае от частоты электромагнитного поля), которые собраны в различных справочниках физических величин[35].
. При этом учитываются индивидуальные свойства среды. На практике в материальных уравнениях обычно используются экспериментально определяемые коэффициенты (зависящие в общем случае от частоты электромагнитного поля), которые собраны в различных справочниках физических величин[35].



 — диэлектрическая восприимчивость и
— диэлектрическая восприимчивость и 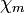 — магнитная восприимчивость вещества (в системе единиц СИ эти константы в
— магнитная восприимчивость вещества (в системе единиц СИ эти константы в  раз больше, чем в гауссовой системе СГС). Соответственно, материальные уравнения для электрической и магнитной индукций записываются в следующем виде:
раз больше, чем в гауссовой системе СГС). Соответственно, материальные уравнения для электрической и магнитной индукций записываются в следующем виде:
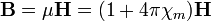


 — относительная диэлектрическая проницаемость,
— относительная диэлектрическая проницаемость, 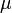 — относительная магнитная проницаемость. Размерные величины
— относительная магнитная проницаемость. Размерные величины  (в единицах СИ — Ф/м) и
(в единицах СИ — Ф/м) и  (в единицах СИ — Гн/м), возникающие в системе СИ, называются абсолютная диэлектрическая проницаемость и абсолютная магнитная проницаемость соответственно.
(в единицах СИ — Гн/м), возникающие в системе СИ, называются абсолютная диэлектрическая проницаемость и абсолютная магнитная проницаемость соответственно.
 — удельная проводимость среды (в единицах СИ — Ом−1•м−1).
— удельная проводимость среды (в единицах СИ — Ом−1•м−1). ,
,  и
и  . В системе координат главных осей они могут быть описаны диагональными матрицами. В этом случае, связь между напряжённостями полей и индукциями имеют различные коэффициенты по каждой координате. Например, в системе СИ:
. В системе координат главных осей они могут быть описаны диагональными матрицами. В этом случае, связь между напряжённостями полей и индукциями имеют различные коэффициенты по каждой координате. Например, в системе СИ: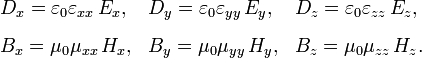


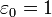 ).
).


