
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторы Римана — ЗильберштейнаСодержание книги
Поиск на нашем сайте
Если ввести комплексный вектор Римана — Зильберштейна
то уравнения Максвелла сводятся к двум:
При отсутствии сторонних зарядов и токов остаётся только второе уравнение (первое из-за равенства дивергенции ротора нулю в этом случае удовлетворяется автоматически с точностью до не зависящей от времени компоненты):
В отличие от волнового уравнения, которое получаются в этом случае для векторов поля или потенциала, последнее векторное дифференциальное уравнение имеет первый, а не второй порядок и поэтому в ряде случаев может быть проще для решения. Для гармонического поля с зависимостью
При выбранной нормировке
имеет смысл плотности энергии поля. Вектор Пойнтинга:
Векторы Ковариантная формулировка С современной точки зрения, четырёхмерная ковариантная формулировка электродинамики, и в частности — запись уравнений Максвелла в таком виде, является физически наиболее фундаментальной. Практически она приводит, кроме явной ковариантности, к значительно большей компактности уравнений, а значит определенной красоте и в ряде случаев удобству, и более органично и прямо включает в себя единство электромагнитного поля. Под ковариантной формулировкой понимают два различающихся, но прямо и непосредственно связанных варианта: лоренц-ковариантная формулировка в плоском пространстве-времени Минковского и общековариантная формулировка для общего случая искривленного пространства-времени (стандартно рассматриваемая в контексте общей теории относительности). Второй вариант отличается от первого тем, что метрика пространства-времени в нём не постоянна (что может означать как присутствие гравитации, так и просто использование более широкого класса координат, например, соответствующих неинерциальным системам отсчета), и во многом сводится к замене обычных производных по (четырехмерным) координатам на ковариантные производные (в значительной части случаев это сводится к механической замене первых на вторые). Кроме прочего, второй вариант позволяет исследовать взаимодействие электромагнитного поля с гравитацией.
Четырёхмерные векторы При ковариантной записи уравнений электродинамики производится переход от трёхмерных векторов и скаляров к четырёхмерным векторам (4-векторы). Независимо от системы единиц, четырёхмерные координаты (4-вектор координат, в компоненты которого входят время и трехмерные пространственные координаты), производная по этим координатам (4-производная) и плотность тока определяются следующим образом[52]:
Индекс 4-вектора принимает значения
По повторяющемуся индексу предполагается суммирование от 0 до 3 (правило Эйнштейна). Пример Приведенное выше уравнение является компактной записью уравнения непрерывности:
Введём 4-вектор потенциала, имеющий в системах СГС и СИ следующие компоненты:
При ковариантной записи играет роль положение индекса у 4-вектора. Если индекс находится внизу, то такой вектор называется ковариантным вектором (или ковектором), и его пространственные компоненты имеют обратный знак по сравнению с компонентами 4-вектора. Поднятие и опускание индексов проводится при помощи метрического тензора При помощи такого определения 4-вектора потенциала, калибровочное условие Лоренца в ковариантной форме можно записать следующим образом:
Если это условие выполняется, то уравнения Максвелла для потенциалов в вакууме при наличии зарядов и токов принимают вид:
где
Нулевая компонента уравнений Максвелла для 4-вектора потенциала соответствует уравнению для
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 487; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.12.30 (0.01 с.) |

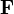 и комплексно сопряжённый ему вектор
и комплексно сопряжённый ему вектор 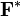 [49][50][51]:
[49][50][51]: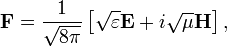
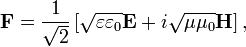
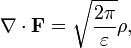
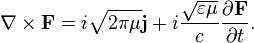
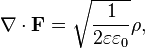
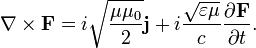
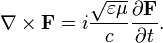
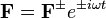 вектор
вектор 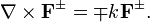
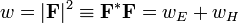
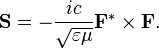
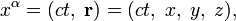
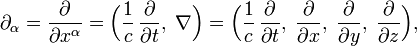
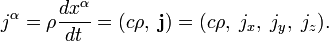
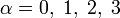 . В компонентной записи вектора сначала идёт нулевая компонента, затем — пространственные. Например, время равно
. В компонентной записи вектора сначала идёт нулевая компонента, затем — пространственные. Например, время равно 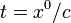 , а плотность заряда
, а плотность заряда 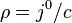 . В силу этих определений, закон сохранения заряда в ковариантной форме принимает следующий вид:
. В силу этих определений, закон сохранения заряда в ковариантной форме принимает следующий вид: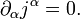
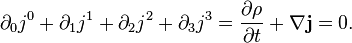
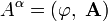
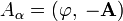
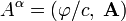
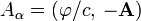
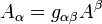 , который в четырёхмерном пространстве Минковского имеет диагональный вид с сигнатурой:
, который в четырёхмерном пространстве Минковского имеет диагональный вид с сигнатурой: 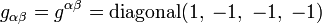 .
.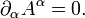
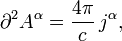
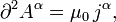
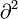 — оператор Даламбера с обратным знаком:
— оператор Даламбера с обратным знаком: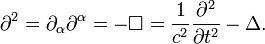
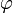 , а пространственная — для
, а пространственная — для 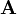 .
.


