
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Единственность решений уравнений МаксвеллаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Уравнения Максвелла являются дифференциальными уравнениями в частных производных. Поэтому для их решения необходимо задать начальные и граничные условия. При фиксированных функциях плотности заряда и тока для нестационарных полей получаемое решение единственно. Этот факт формулируется в виде теоремы[73][74][75]: Если напряженности электрического и магнитного полей заданы в начальный момент времени Доказательство Пусть электрическая и магнитная индукции связаны с напряжённостями полей при помощи следующих материальных уравнений:
где
где индекс указывает номер решения. Так как начальные и граничные условия заданы (одинаковые для обоих возможных решений), то:
Первые соотношения соответствуют начальным условиям, в вторые — граничным условиям на поверхности
где коэффициент Предположим, что не равны нулю оба разностных поля. Если первое уравнение умножить на
Это выражение можно проинтегрировать по объёму
Тангенциальные (касательные) к поверхности
Полученное соотношение интегрируется по времени. Так как в начальный момент времени
Подынтегральная функция является положительно определённой (всегда больше или равна нулю). Интеграл от такой функции равен нулю, только в том случае когда подынтегральная функция тождественно равна нулю. Следовательно, в любой момент времени внутри объёма Для единственности решения уравнений Максвелла вместо задания тангенциальных компонент поля можно потребовать выполнение на границе условия импедансного типа
где импеданс Для гармонических во времени процессов единственность решения задачи без начальных условий обеспечивается сколь угодно малым поглощением энергии внутри объёма В стационарных задачах электростатики и магнитостатики единственное решение для установившихся полей определяется только граничными условиями.
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 507; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.77.244 (0.01 с.) |

 в каждой точке некоторой области пространства
в каждой точке некоторой области пространства  и в течениe всего времени
и в течениe всего времени 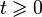 заданы тангенциальные (касательные) составляющие напряженности электрического или магнитного поля на границе этой области
заданы тангенциальные (касательные) составляющие напряженности электрического или магнитного поля на границе этой области  , то существует единственное решение уравнений Максвелла.
, то существует единственное решение уравнений Максвелла.
 и
и  — положительно определённые, симметричные, стационарные матрицы. Если при данных начальных и граничных условиях существуют два различных решения, то следующие величины будут отличны от нуля:
— положительно определённые, симметричные, стационарные матрицы. Если при данных начальных и граничных условиях существуют два различных решения, то следующие величины будут отличны от нуля:

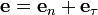 . (Индекс
. (Индекс  — нормальная составляющая к поверхности, а
— нормальная составляющая к поверхности, а 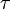 — касательная. Аналогично для
— касательная. Аналогично для  ) Подстановка функций
) Подстановка функций  и
и  в уравнения Максвелла для роторов приводит к следующим уравнениям:
в уравнения Максвелла для роторов приводит к следующим уравнениям:
 равен
равен  в системе СГС и единице в системе СИ. Если одно из разностных полей
в системе СГС и единице в системе СИ. Если одно из разностных полей  или
или 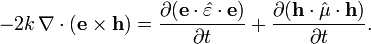

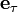 или
или  при любом
при любом 
 , то константа интегрирования равна нулю, и при любом
, то константа интегрирования равна нулю, и при любом 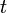 :
:
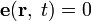 и
и 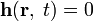 . Поэтому решения совпадают.
. Поэтому решения совпадают.
 выбран так, чтобы исключить приток энергии извне. Такое условие позволяет сформулировать теорему единственности и в неограниченном случае, при этом импедансное условие обращается в условие излучения Зоммерфельда на бесконечности.
выбран так, чтобы исключить приток энергии извне. Такое условие позволяет сформулировать теорему единственности и в неограниченном случае, при этом импедансное условие обращается в условие излучения Зоммерфельда на бесконечности.


