
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плоские электромагнитные волныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
где
и они перпендикулярны вектору
Вывод решения для плоской волны [показать] Если напряжённость электрического поля зависит от координат и времени в виде следующей их комбинации
и аналогично для магнитной индукции. Поэтому уравнения Максвелла в отсутствие зарядов и токов принимают вид (система СИ):
Интегрируя эти соотношения по
Подставляя четвёртое уравнение в третье, получаем Физический смысл решения в виде плоской волны состоит в следующем. Выберем ось
Предположим, что в начальный момент времени В электромагнитной волне в общем случае напряжённость поля может быть произвольной непериодической функцией
Вектор Пойнтинга (плотность потока энергии), независимо от системы единиц, связан с полной плотностью энергии следующим образом:
Это соотношение соответствует уравнению связи импульса и энергии для безмассовой частицы в релятивистской теории. Однако, скорость
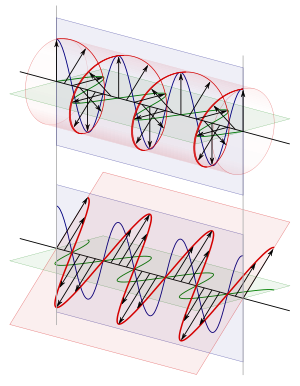
Циркулярно и линейно поляризованная плоская электромагнитная волна Плоские и поперечные волны являются математическими абстракциями. Реальные волны конечной апертуры из-за эффекта дифракции можно считать плоскими и поперечными лишь в некотором приближении.
Выберем координатную ось
Сравнение с общим решением для плоской волны, приводит к следующей связи между вектором
В этом случае, вектор
Константы В фиксированной точке пространства ( Связь с другими теориями Уравнения Максвелла полностью совместимы с принципами специальной теории относительности. Они также применимы при микроскопическом описании вещества, когда заряженные частицы подчиняются принципам квантовой механики, а электромагнитное поле остаётся классическим (не квантовым). В этом случае квантовые объекты (например, электроны) описываются уравнением Шрёдингера или уравнением Дирака, однако, потенциалы электромагнитного взаимодействия в этих уравнениях определяются классическими уравнениями Максвелла.
Тем не менее, существуют явления, для описания которых требуется более последовательное объединение полевого подхода Фарадея — Максвелла с принципами квантовой механики. Оно осуществляется при помощи методов квантовой теории поля в квантовой электродинамике. В этом случае форма уравнений Максвелла (лагранжиан) остаётся неизменной, однако поля становятся операторами, а уравнения Максвелла — операторными уравнениями Гейзенберга. Решение подобных уравнений приводит к появлению новых эффектов, отсутствующих в классической теории поля. Эти эффекты существенны, в частности, в следующих физических ситуациях:
Аксиоматический подход Исторически уравнения Максвелла возникли в результате обобщения различных экспериментальных открытий. Однако с аксиоматической точки зрения их можно получить при помощи следующей последовательности шагов[69]:
Второй подход основан на лагранжевом формализме[70]. При этом постулируется, что электромагнитное поле описывается линейным взаимодействием четырёхмерного потенциала
Как в первом, так и во втором подходе предполагаются установленными принципы теории относительности. Хотя исторически она возникла на основе уравнений Максвелла и второго постулата Эйнштейна, известен, восходящий к работам Игнатовского [71], Франка и Роте[72], аксиоматический способ построения СТО, не использующий постулата об инвариантности скорости света и уравнений Максвелла. В обоих аксиоматических подходах получаются уравнения Максвелла в вакууме при наличии свободных зарядов. Расширение этих уравнений на электродинамику сплошных сред требует дальнейшего привлечения различных модельных представлений о структуре вещества.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 458; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.4.227 (0.011 с.) |

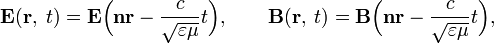
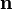 — некоторый постоянный вектор. В этом случае
— некоторый постоянный вектор. В этом случае 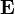 и
и 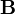 удовлетворяют уравнениям Максвелла в отсутствие зарядов и токов, если между ними существует следующая связь:
удовлетворяют уравнениям Максвелла в отсутствие зарядов и токов, если между ними существует следующая связь: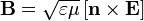
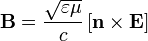
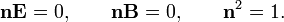
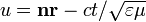 , то для производной
, то для производной 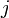 -той компоненты вектора
-той компоненты вектора 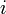 -той координате и времени можно записать:
-той координате и времени можно записать: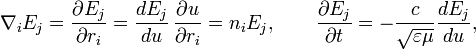
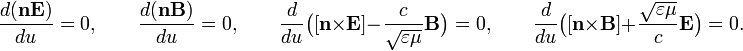
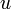 и опуская константы интегрирования, которые соответствуют постоянным полям, получаем:
и опуская константы интегрирования, которые соответствуют постоянным полям, получаем: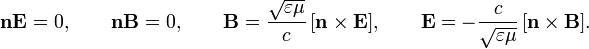
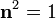 .
.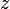 декартовой системы координат так, чтобы вектор
декартовой системы координат так, чтобы вектор 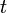 следующим образом:
следующим образом: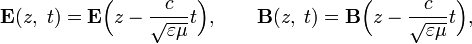
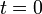 , напряжённость поля является произвольной векторной функцией
, напряжённость поля является произвольной векторной функцией 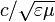 .
.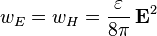
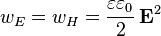
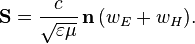
 .
.

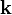 . Тогда вектор электрического поля (как, впрочем, и магнитного) будет лежать в плоскости
. Тогда вектор электрического поля (как, впрочем, и магнитного) будет лежать в плоскости 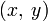 , то есть
, то есть 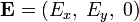 . Если по каждой проекции в этой плоскости электрическое поле совершает периодические колебания, то такую волну называют монохроматической плоской волной:
. Если по каждой проекции в этой плоскости электрическое поле совершает периодические колебания, то такую волну называют монохроматической плоской волной:
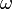 , которое называется уравнением дисперсии:
, которое называется уравнением дисперсии: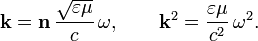
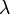 и её частотой
и её частотой 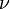 следующим образом:
следующим образом: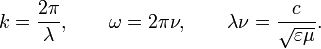
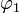 и
и 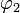 являются сдвигами фазы, а
являются сдвигами фазы, а 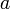 и
и 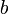 — амплитудами колебаний вдоль каждой оси.
— амплитудами колебаний вдоль каждой оси.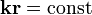 ) вектор электрического поля, в общем случае, описывает в плоскости
) вектор электрического поля, в общем случае, описывает в плоскости 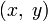 эллипс, поэтому такие волны называются эллиптически поляризованными. Их частным случаем являются волны поляризованные по кругу. Вырожденный в прямую эллипс соответствует колебаниям напряжённости поля вдоль одной прямой в плоскости
эллипс, поэтому такие волны называются эллиптически поляризованными. Их частным случаем являются волны поляризованные по кругу. Вырожденный в прямую эллипс соответствует колебаниям напряжённости поля вдоль одной прямой в плоскости 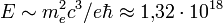 В/м, где
В/м, где 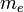 — масса электрона,
— масса электрона,  — его заряд,
— его заряд, 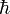 — постоянная Планка) — работа такого поля на комптоновской длине волны электрона равна по порядку величины энергии покоя электрона, что приводит к самопроизвольной генерации электрон-позитронных пар из вакуума (эффект Швингера)[66]. В результате возникает эффективное взаимодействие фотонов, которое отсутствует в классической электродинамике, приводящее к эффективному изменению лагранжиана поля (например, в низкоэнергетическом пределе поле описывается лагранжианом Гейзенберга — Эйлера[67]).
— постоянная Планка) — работа такого поля на комптоновской длине волны электрона равна по порядку величины энергии покоя электрона, что приводит к самопроизвольной генерации электрон-позитронных пар из вакуума (эффект Швингера)[66]. В результате возникает эффективное взаимодействие фотонов, которое отсутствует в классической электродинамике, приводящее к эффективному изменению лагранжиана поля (например, в низкоэнергетическом пределе поле описывается лагранжианом Гейзенберга — Эйлера[67]).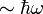 , где
, где 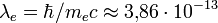 м, когда в результате вакуумных эффектов, модифицируется, например, закон Кулона.
м, когда в результате вакуумных эффектов, модифицируется, например, закон Кулона.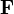 , действующая на пробный заряд
, действующая на пробный заряд 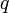 со стороны неподвижного заряда
со стороны неподвижного заряда 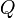 );
);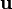 заряда
заряда 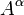 , с четырёх-вектором электрического тока
, с четырёх-вектором электрического тока 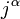 , а свободный лагранжиан пропорционален инвариантной свёртке квадрата тензора электромагнитного поля
, а свободный лагранжиан пропорционален инвариантной свёртке квадрата тензора электромагнитного поля 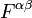 .
.


