
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вывод уравнения непрерывностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Дивергенция от ротора равна нулю, поэтому для четвёртого уравнения Максвелла (закон Ампера — Максвелла) в системе СИ имеем:
где в последнем равенстве подставлено первое уравнение (закон Гаусса). Это уравнение при помощи интегральной теоремы Остроградского — Гаусса можно записать в следующем виде:
В левой части уравнения находится полный ток, протекающий через замкнутую поверхность Уравнение непрерывности, эквивалентное закону сохранения заряда, далеко выходит за пределы классической электродинамики, оставаясь справедливым и в квантовой теории. Это уравнение само по себе может быть положено в основу (быть выбрано одним из решающих постулатов) электромагнитной теории. Из уравнений Максвелла для роторов и уравнения непрерывности с точностью до произвольных функций, не зависящих от времени, следуют законы Гаусса для электрического и магнитного полей. Закон сохранения энергии Если умножить третье уравнение Максвелла в дифференциальной форме (закон Фарадея) скалярно на
где
Вывод теоремы Пойнтинга При помощи третьего и четвёртого уравнения Максвелла в дифференциальной форме, в системе СИ можно получить:
Разница левых частей уравнений сворачивается по следующей формуле векторного анализа (производная произведения):
В линейных, но, возможно, неизотропных средах, между напряжённостями и индукциями существует линейная связь. Например, для электрического поля
Аналогично для магнитного поля. Вектор Величины
Это уравнение показывает, что при отсутствии внутренних потерь изменение энергии электромагнитного поля в объёме происходит только за счёт мощности электромагнитного излучения, переносимого через границу этого объёма.
|
||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 452; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.72.244 (0.006 с.) |



 . В правой части — изменение со временем заряда, находящегося внутри объёма
. В правой части — изменение со временем заряда, находящегося внутри объёма  . Таким образом, изменение заряда внутри объёма возможно только при его притоке или оттоке через поверхность
. Таким образом, изменение заряда внутри объёма возможно только при его притоке или оттоке через поверхность 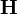 , а четвёртое (закон Ампера — Максвелла) на
, а четвёртое (закон Ампера — Максвелла) на  и сложить результаты, можно получить теорему Пойнтинга:
и сложить результаты, можно получить теорему Пойнтинга:



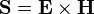
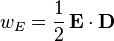



 . Если
. Если  симметричная матрица, не зависящая от времени, то:
симметричная матрица, не зависящая от времени, то:
 называется вектором Пойнтинга (вектором плотности потока электромагнитной энергии) и определяет количество электромагнитной энергии, переносимой через единицу площади в единицу времени. Интеграл вектора Пойнтинга по сечению распространяющейся волны определяет её мощность. Важно отметить, что, как впервые указал Хевисайд, физический смысл потока энергии имеет только безвихревая часть вектора Пойнтинга. Вихревая часть, дивергенция которой равна нулю, не связана с переносом энергии. Заметим, что Хевисайд получил выражение для закона сохранения независимо от Пойнтинга. В русскоязычной литературе вектор Пойнтинга часто называется также «вектором Умова — Пойнтинга».
называется вектором Пойнтинга (вектором плотности потока электромагнитной энергии) и определяет количество электромагнитной энергии, переносимой через единицу площади в единицу времени. Интеграл вектора Пойнтинга по сечению распространяющейся волны определяет её мощность. Важно отметить, что, как впервые указал Хевисайд, физический смысл потока энергии имеет только безвихревая часть вектора Пойнтинга. Вихревая часть, дивергенция которой равна нулю, не связана с переносом энергии. Заметим, что Хевисайд получил выражение для закона сохранения независимо от Пойнтинга. В русскоязычной литературе вектор Пойнтинга часто называется также «вектором Умова — Пойнтинга». и
и  определяют объёмные плотности энергии, соответственно, электрического и магнитного полей. При отсутствии токов и связанных с ними потерь теорема Пойнтинга является уравнением непрерывности для энергии электромагнитного поля. Проинтегрировав его в этом случае по некоторому замкнутому объёму и воспользовавшись теоремой Остроградского — Гаусса, можно получить закон сохранения энергии для электромагнитного поля:
определяют объёмные плотности энергии, соответственно, электрического и магнитного полей. При отсутствии токов и связанных с ними потерь теорема Пойнтинга является уравнением непрерывности для энергии электромагнитного поля. Проинтегрировав его в этом случае по некоторому замкнутому объёму и воспользовавшись теоремой Остроградского — Гаусса, можно получить закон сохранения энергии для электромагнитного поля:



