
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скалярный и векторный потенциалыСодержание книги
Поиск на нашем сайте
Закон Фарадея и закон Гаусса для магнитной индукции выполняются тождественно, если электрическое и магнитное поля выразить через скалярный
Доказательство Если магнитное поле равно ротору векторного потенциала, то дивергенция автоматически равна нулю:
Подставляя выражение для напряжённости электрического поля в закон Фарадея, например, в системе СИ, получаем:
При данных электрическом
Подобные преобразования играют важную роль в квантовой электродинамике и лежат в основе локальной калибровочной симметрии электромагнитного взаимодействия. Локальная калибровочная симметрия вводит зависимость от координат и времени в фазу глобальной калибровочной симметрии, которая, в силу теоремы Нётер, приводит к закону сохранения заряда. Неоднозначность определения потенциалов оказывается удобной для наложения на них дополнительных условий, называемых калибровкой. Благодаря этому, уравнения электродинамики принимают более простой вид. Рассмотрим, например, уравнения Максвелла в однородных и изотропных средах с диэлектрической (
В этом случае оставшиеся уравнения Максвелла в однородных и изотропных средах могут быть записаны в следующем виде:
где
Таким образом, 8 уравнений Максвелла для компонент электромагнитного поля (2 векторных и 2 скалярных) при помощи потенциалов могут быть сведены к 4 уравнениям (скалярному для Возможно введение других калибровок. Так, для решения ряда задач удобной оказывается кулоновская калибровка:
В этом случае:
где Первое уравнение описывает мгновенное (без запаздывания) действие кулоновской силы, поскольку кулоновская калибровка неинвариантна относительно преобразований Лоренца. При этом энергию кулоновского взаимодействия можно отделить от остальных взаимодействий, что облегчает квантование поля в гамильтоновом формализме[42]. Векторный потенциал играет большую роль в электродинамике и в квантовой теории поля, однако для исследования процессов распространения электромагнитных волн в отсутствие токов и зарядов его введение часто не приводит к упрощению системы, а сводится к простой замене векторов электрического и магнитного поля на другой аналогичный вектор, описываемый теми же уравнениями. Так, для гармонических полей векторный потенциал будет просто пропорционален электрическому полю (скалярный потенциал при этом можно положить равным нулю). Векторы Герца
Заметим, что скалярный Подставляя выражения для полей через электрический вектор в два последних уравнения Максвелла, можно получить[43][44]:
Здесь введён вектор поляризации свободных зарядов и токов:
(при этом уравнение непрерывности для заряда автоматически выполняется). Таким образом, электрический вектор Герца определяется волновыми уравнениями, в правой части которых стоит поляризуемость, обусловленная свободными, либо свободными и связанными зарядами, то есть электрическими дипольными моментами.
Поскольку поля, описываемые магнитным вектором Герца, не зависят от свободных зарядов и токов, а магнитные монополи не обнаружены, потенциалы удовлетворяют калибровке Лоренца в вырожденном виде — так называемой кулоновской калибровке ( Аналогичным образом можно получить уравнения для магнитного потенциала Герца, подставляя выраженные через него поля в третье и четвёртое уравнения Максвелла без тока:
Действие сторонних магнитных полей, связанных с внешними источниками, может быть учтено по аналогии с электрическим вектором Герца введением в правые части дополнительной магнитной поляризации Таким образом, выделяется два типа электромагнитных полей, выражающихся через электрический и магнитный потенциалы Герца, а произвольное поле можно представить в виде суммы таких полей. Поля, выражающиеся через электрический вектор Герца носят название полей электрического типа или поперечно-магнитных ( Потенциалы Дебая В электродинамике широко используются скалярные потенциалы, предложенные Дебаем[46]. Волновое уравнение представляет собой систему трёх связанных скалярных уравнений, которые распадаются на три скалярных уравнения Гельмгольца только в декартовой системе координат. Для удобства поиска решений, удовлетворяющих граничным условиям желательно выбирать координатные системы, координатные поверхности которых близки или совпадают с поверхностями границ. Один из подходов к решению векторного уравнения Гельмгольца состоит во введении скалярных функций
Здесь Если для некоторой ортогональной координатной системы существует функция Такое представление возможно только в ограниченном числе ортогональных координатных систем[48]. В декартовой системе координат в качестве вектора
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 917; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.25.125 (0.008 с.) |

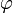 и векторный
и векторный 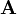 потенциалы[39]:
потенциалы[39]:




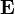 и магнитном
и магнитном 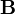 полях, скалярный и векторный потенциалы определены неоднозначно. Если
полях, скалярный и векторный потенциалы определены неоднозначно. Если  — произвольная функция координат и времени, то следующее преобразование не изменит значение полей:
— произвольная функция координат и времени, то следующее преобразование не изменит значение полей:


 ) и магнитной (
) и магнитной (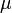 ) проницаемостями. Для данных
) проницаемостями. Для данных  , чтобы выполнялось калибровочное условие Лоренца [40]:
, чтобы выполнялось калибровочное условие Лоренца [40]:
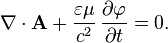
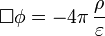
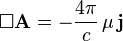

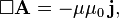
 — оператор Д’Аламбера, который и в системе СГС, и в системе СИ имеет вид:
— оператор Д’Аламбера, который и в системе СГС, и в системе СИ имеет вид:





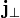 — соленоидальная часть тока (
— соленоидальная часть тока ( ).
). и позволяет в некоторых случаях упростить решение электродинамических задач, сводя их к решению скалярного волнового уравнения.
и позволяет в некоторых случаях упростить решение электродинамических задач, сводя их к решению скалярного волнового уравнения.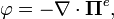

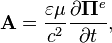
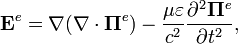
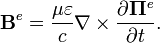


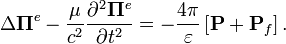
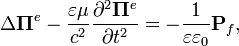



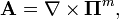

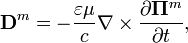


 ,
, 

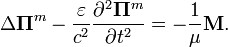
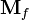 .
.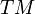 ) полей, поскольку магнитное поле для них ортогонально направлению вектора Герца. Соответственно, поля, выражающиеся через магнитный вектор Герца, называют полями магнитного типа или поперечно-электрическими полями (
) полей, поскольку магнитное поле для них ортогонально направлению вектора Герца. Соответственно, поля, выражающиеся через магнитный вектор Герца, называют полями магнитного типа или поперечно-электрическими полями (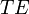 ), электрическое поле в которых ортогонально порождающему вектору Герца. Поля
), электрическое поле в которых ортогонально порождающему вектору Герца. Поля 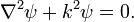



 — некоторая векторная функция координат. Вектор
— некоторая векторная функция координат. Вектор 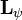 , описывает потенциальную часть поля и его можно положить равным нулю при отсутствии свободных зарядов.
, описывает потенциальную часть поля и его можно положить равным нулю при отсутствии свободных зарядов. , пропорциональная координатному вектору, то произвольное векторное поле, удовлетворяющее векторному уравнению Гельмгольца в этой системе, можно представить в виде суммы векторных функций, пропорциональных векторам
, пропорциональная координатному вектору, то произвольное векторное поле, удовлетворяющее векторному уравнению Гельмгольца в этой системе, можно представить в виде суммы векторных функций, пропорциональных векторам  и
и  . Как следует из уравнений Максвелла, электрическому полю, пропорциональному
. Как следует из уравнений Максвелла, электрическому полю, пропорциональному  соответствуют векторам Герца. Поскольку в этом случае поле, пропорциональное
соответствуют векторам Герца. Поскольку в этом случае поле, пропорциональное  , для сферической
, для сферической  . Кроме того, такое представление возможно в конической, а также относительно оси
. Кроме того, такое представление возможно в конической, а также относительно оси 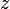 в параболической и эллиптической цилиндрических системах координат.
в параболической и эллиптической цилиндрических системах координат.


