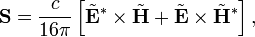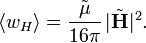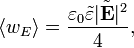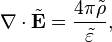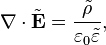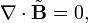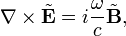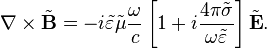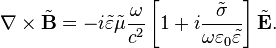Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Запись при помощи дифференциальных форм
Основная статья: Дифференциальные формы в электромагнетизме Уравнения Максвелла в ковариантной форме, аналогично векторному представлению в трёхмерном пространстве, можно записать в «безындексной форме». Для этого вводится операция внешнего произведения
Из 1-формы, при помощи операции внешнего дифференцирования
Операция внешнего дифференцирования обладает свойством
Для записи оставшихся уравнений Максвелла вводится дуальная к
и 3-форма тока:
где В этих обозначениях уравнения Максвелла в системах СГС и СИ принимают следующий вид[63]:
Доказательство Чтобы показать эквивалентность этих уравнений уравнениям Максвелла, необходимо записать их в трёхмерной векторной форме. В этом случае, в системе СГС, ток и 2-форма Максвелла имеют вид:
где
то, с учётом уравнений Максвелла в дифференциальной форме, получим С учётом тождества
В такой форме уравнения Максвелла остаются справедливыми и на произвольном 4-мерном многообразии, например, в искривлённом пространстве-времени общей теории относительности. В этом случае, в соотношениях дополнительно появляется определитель метрического тензора
Общековариантная запись в компонентах На произвольном 4-мерном многообразии, то есть в общем случае, включающем и пространство-время ненулевой кривизны (а также произвольных четырёхмерных координат, включая случаи неинерциальных систем отсчета) электродинамика может быть сформулирована и в обычных индексных обозначениях.
В основном рецепт перехода от случая нулевой кривизны пространства-времени и лоренцевых систем отсчета в нём, подробно описанного выше, к общему случаю состоит в замене обычных производных по координатам на ковариантные производные, учет того, что метрика в этом случае не постоянна и не имеет специального лоренцева вида (то есть практически произвольна), а также при интегрировании — например, при записи действия — учёт того, что метрика входит в элемент объёма (через множитель Спектральное представление В электродинамике большое значение имеют гармонические колебания. Такие поля можно представить в виде:
где Усреднённые за период плотности энергии электрического и магнитного поля равны, соответственно:
Используя преобразование Фурье, по гармоническим колебаниям можно разложить поля с произвольной временной зависимостью.
Переход к спектральным компонентам позволяет сосредоточиться на координатной зависимости полей. Уравнения Максвелла для спектральных компонент в однородных средах при этом принимают вид:
Диэлектрическая и магнитная проницаемости среды в спектральном представлении связаны с восприимчивостью материальных уравнений в интегральном представлении Фурье-преобразованием:
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 274; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.42.168 (0.005 с.) |
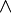 , обладающая свойством антисимметричности
, обладающая свойством антисимметричности 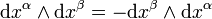 . Внешнее произведение позволяет записывать свёрнутые по всем индексам выражения с антисимметричными тензорами, такими как
. Внешнее произведение позволяет записывать свёрнутые по всем индексам выражения с антисимметричными тензорами, такими как  . При этом возникают объекты, называемые дифференциальными формами (или просто формами)[61]. 1-форма потенциала поля определяется следующим образом (по индексу
. При этом возникают объекты, называемые дифференциальными формами (или просто формами)[61]. 1-форма потенциала поля определяется следующим образом (по индексу  — сумма от 0 до 3):
— сумма от 0 до 3):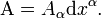
 , получается 2-форма электромагнитного поля (или 2-форма Фарадея):
, получается 2-форма электромагнитного поля (или 2-форма Фарадея):
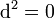 , что приводит к закону Гаусса для магнитного поля и закону Фарадея:
, что приводит к закону Гаусса для магнитного поля и закону Фарадея: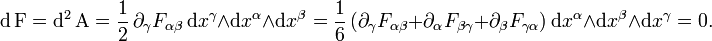
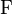 2-форма
2-форма 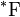 , называемая также 2-формой Максвелла[62]:
, называемая также 2-формой Максвелла[62]: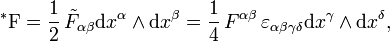
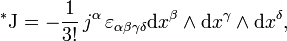
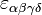 — абсолютный антисимметричный символ Леви-Чивиты (
— абсолютный антисимметричный символ Леви-Чивиты ( ). Свёртка с символом Леви-Чевиты внешнего произведения дифференциалов называется оператором звезды Ходжа.
). Свёртка с символом Леви-Чевиты внешнего произведения дифференциалов называется оператором звезды Ходжа.

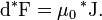

 — трёхмерный объём, а
— трёхмерный объём, а 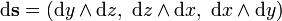 — вектор площади поверхности в трёхмерном пространстве. Так как:
— вектор площади поверхности в трёхмерном пространстве. Так как:
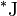 .
.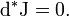
 . Например, для тока и внешнего дифференцирования:
. Например, для тока и внешнего дифференцирования: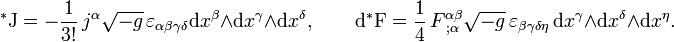
 — корень из минус детерминанта метрики).
— корень из минус детерминанта метрики).

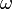 — частота колебаний поля. Обозначение «c. c.» означает комплексное сопряжение предыдущего слагаемого. В некоторых работах коэффициент 1/2 в соглашении о гармонических амплитудах не используется, что приводит к соответствующей модификации всех связанных с этим соглашением выражений. В литературе также часто встречается выбор обратного знака в комплексной экспоненте. Рассмотренный здесь вариант согласуется с принятым в квантовой теории в представлении Шрёдингера.
— частота колебаний поля. Обозначение «c. c.» означает комплексное сопряжение предыдущего слагаемого. В некоторых работах коэффициент 1/2 в соглашении о гармонических амплитудах не используется, что приводит к соответствующей модификации всех связанных с этим соглашением выражений. В литературе также часто встречается выбор обратного знака в комплексной экспоненте. Рассмотренный здесь вариант согласуется с принятым в квантовой теории в представлении Шрёдингера.