
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тензор электромагнитного поляСодержание книги
Поиск на нашем сайте Определим ковариантный тензор электромагнитного поля при помощи производной от 4-вектора потенциала[53][54]:
Явный вид этого антисимметричного тензора (
Временные компоненты тензора составлены из компонент напряжённости электрического поля, а пространственные — магнитного, что может быть записано следующим образом: Используя определение тензора электромагнитного поля, несложно проверить выполнение следующего тождества:
Его можно переписать в более компактном виде, введя дуальный тензор электромагнитного поля:
где Полная система уравнений Максвелла в ковариантной форме имеет вид:
По повторяющемуся индексу При помощи тензора электромагнитного поля можно получить законы преобразований компонент электрического и магнитного полей, измеряемых относительно различных инерциальных систем отсчёта[56][57]:
где «штрихованные» величины измеряются относительно системы отсчёта, движущейся вдоль оси Уравнения Максвелла в вакууме инвариантны относительно преобразований Лоренца. Это послужило одним из толчков к созданию специальной теории относительности. Электрическое и магнитное поля различным образом изменяются при инверсии осей пространственной системы координат. Электрическое поле является полярным вектором, а магнитное — аксиальным вектором. Можно построить две инвариантные относительно преобразований Лоренца величины:
Первый инвариант является скаляром, а второй — псевдоскаляром, то есть изменяет свой знак при инверсии координатных осей. Лагранжиан Действие
где:
Уравнения движения заряда под воздействием силы Лоренца в ковариантной записи имеют вид:
Уравнения Максвелла получаются из принципа наименьшего действия, в котором динамическими переменными являются 4-х потенциалы электромагнитного поля
где производится интегрирование по инвариантному 4-объёму
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 733; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.006 с.) |


 ) может быть представлен в следующем виде:
) может быть представлен в следующем виде:
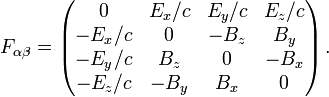
 . В тензоре электромагнитного поля с верхними индексами изменяется знак у нулевых компонент (то есть перед компонентами электрического поля):
. В тензоре электромагнитного поля с верхними индексами изменяется знак у нулевых компонент (то есть перед компонентами электрического поля):  .
.
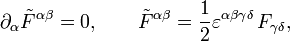
 — антисимметричный символ Леви-Чивиты (
— антисимметричный символ Леви-Чивиты ( ). Это уравнение является ковариантной записью закона Гаусса для магнитного поля и закона электромагнитной индукции Фарадея. Компоненты дуального тензора
). Это уравнение является ковариантной записью закона Гаусса для магнитного поля и закона электромагнитной индукции Фарадея. Компоненты дуального тензора  получаются из тензора
получаются из тензора  в результате перестановки электрического и магнитного полей[55]:
в результате перестановки электрического и магнитного полей[55]:  ,
, 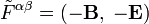 .
.
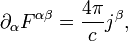
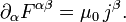
 проводится суммирование от 0 до 3, а в правой части второго уравнения находится 4-вектор тока. Нулевая компонента этого уравнения соответствует закону Гаусса, а пространственные — закону Ампера — Максвелла.
проводится суммирование от 0 до 3, а в правой части второго уравнения находится 4-вектор тока. Нулевая компонента этого уравнения соответствует закону Гаусса, а пространственные — закону Ампера — Максвелла.


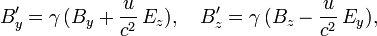
 со скоростью
со скоростью 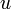 относительно системы, в которой измеряются «не штрихованные» компоненты полей, а
относительно системы, в которой измеряются «не штрихованные» компоненты полей, а 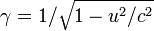 — фактор Лоренца. Компоненты полей вдоль направления относительного движения инерциальных систем отсчёта остаются неизменными:
— фактор Лоренца. Компоненты полей вдоль направления относительного движения инерциальных систем отсчёта остаются неизменными:  .
.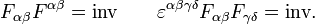
 и лагранжиан (функция Лагранжа)
и лагранжиан (функция Лагранжа) 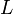 для пробного заряда, двигающегося во внешнем электромагнитном поле в системе СГС и СИ имеют вид[58] [59]:
для пробного заряда, двигающегося во внешнем электромагнитном поле в системе СГС и СИ имеют вид[58] [59]: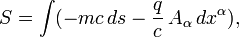
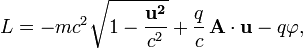

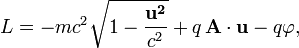
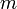 — масса частицы (в единицах СИ — кг);
— масса частицы (в единицах СИ — кг);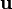 — её скорость (в единицах СИ — м/с);
— её скорость (в единицах СИ — м/с);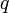 — заряд частицы (в единицах СИ — Кл);
— заряд частицы (в единицах СИ — Кл);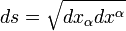 — 4-интервал.
— 4-интервал.

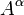 . При этом используется следующее ковариантное выражение для действия[59][60]:
. При этом используется следующее ковариантное выражение для действия[59][60]:
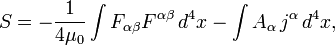
 .
.


