Избрание в Королевское общество

В 1824 Фарадей был избран членом Королевского общества, несмотря на активное противодействие Дэви, отношения с которым стали у Фарадея к тому времени довольно сложными, хотя Дэви любил повторять, что из всех его открытий самым значительным было «открытие Фарадея». Последний также воздавал должное Дэви, называя его «великим человеком». Спустя год после избрания в Королевское общество Фарадея назначают директором лаборатории Королевского института, а в 1827 он получает в этом институте профессорскую кафедру.

Фарадей и религия

Майкл Фарадей был верующим христианином и продолжал верить даже после того, как узнал о работах Дарвина. Он принадлежал к сандиманианской (англ.) секте, члены которой интерпретировали Библию буквально. Учёный был выбран старейшиной секты в 1840 году, однако в 1844 году вместе с ещё 13 человек был из неё исключён по неизвестным причинам. Однако уже через несколько недель Фарадей был принят обратно. Несмотря на то, что в 1850 году он снова был на грани исключения из секты, что, по её правилам, означало бы пожизненное исключение, в 1860 году Фарадей был выбран старейшиной во второй раз. На этом посту он находился до 1864 года^[5].

Труды в русских переводах

• Фарадей М. Избранные работы по электричеству. М.-Л.: ГОНТИ, 1939. Серия: Классики естествознания. (Сборник разных работ и фрагментов).
• Фарадей М. Силы материи и их взаимоотношения. М.: ГАИЗ, 1940.
• Фарадей М. Экспериментальные исследования по электричеству. В 3 тт. М.: Изд. АН СССР, 1947, 1951, 1959. (Оригинальное название: Experimental Researches in Electricity).

• Клетка Фарадея
• Фарад
• Фарадей (единица измерения)
• Закон электромагнитной индукции Фарадея

Примечания

1. ↑ ГРАМОТА.РУ – справочно-информационный интернет-портал «Русский язык»
2. ↑ Frank A. J. L. James, ‘Faraday, Michael (1791—1867)’, Oxford Dictionary of National Biography, Oxford University Press, Sept 2004; Jan 2008
3. ↑ ФАРАДЕЙ, МАЙКЛ — статья из энциклопедии «Кругосвет»
4. ↑ ¹²³⁴⁵ К истории открытия явления электромагнитной индукции // Санкт-Петербургская школа
5. ↑ Frank A. J. L. James Michael Faraday. — Oxford University Press, 2011. — С. 15—17. — 162 с. — (Very Short Introductions). — ISBN 0199574316

Литература

• Радовский М. И. Фарадей. М.: Журнально-газетное объединение, 1936. Серия: Жизнь замечательных людей, выпуск 19-20 (91-92).

Ссылки

• Майкл Фарадей. История свечи
• Майкл Фарадей
• Биографии химиков. Фарадей
• Статья в энциклопедии «Кругосвет»
• Майкл Фарадей
• Майкл Фарадей — биография
• «Король экспериментаторов»
• Опыты Фарадея (видеоролик с демонстрациями)

 

 

Уравнения Максвелла.

Уравнения Максвелла

Материал из Википедии — свободной энциклопедии

Уравне́ния Ма́ксвелла — система дифференциальных уравнений, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах. Вместе с выражением для силы Лоренца образуют полную систему уравнений классической электродинамики. Уравнения, сформулированные Джеймсом Клерком Максвеллом на основе накопленных к середине XIX века экспериментальных результатов, сыграли ключевую роль в развитии представлений теоретической физики и оказали сильное, зачастую решающее, влияние не только на все области физики, непосредственно связанные с электромагнетизмом, но и на многие возникшие впоследствии фундаментальные теории, предмет которых не сводился к электромагнетизму (одним из ярчайших примеров здесь может служить специальная теория относительности).

Содержание 1 История 2 Запись уравнений Максвелла и системы единиц 3 Дифференциальная форма 4 Интегральная форма 5 Сила Лоренца 6 Размерные константы в уравнениях Максвелла 7 Уравнения Максвелла в среде 7.1 Связанные заряды и токи 7.2 Материальные уравнения 7.3 Уравнения в изотропных и однородных средах без дисперсии 7.4 Граничные условия 8 Законы сохранения 8.1 Уравнение непрерывности для зарядов и токов (сохранение заряда) 8.2 Закон сохранения энергии 8.3 Импульс электромагнитного поля 9 Потенциалы 9.1 Скалярный и векторный потенциалы 9.2 Векторы Герца 9.3 Потенциалы Дебая 9.4 Векторы Римана — Зильберштейна 10 Ковариантная формулировка 10.1 Четырёхмерные векторы 10.2 Тензор электромагнитного поля 10.3 Лагранжиан 10.4 Запись при помощи дифференциальных форм 10.5 Общековариантная запись в компонентах 11 Спектральное представление 12 Уравнения без свободных зарядов и токов 12.1 Волновое уравнение 12.2 Уравнение Гельмгольца 13 Некоторые точные решения 13.1 Поле движущегося точечного заряда 13.2 Плоские электромагнитные волны 14 Связь с другими теориями 15 Аксиоматический подход 16 Единственность решений уравнений Максвелла 17 Численное решение уравнений Максвелла 18 Источники 19 Примечания 20 См. также 21 Литература 21.1 Исторические публикации 21.2 История развития 21.3 Общие курсы физики 21.4 Курсы теоретической физики 21.5 Решения уравнений Максвелла 22 Ссылки

История

Джеймс Клерк Максвелл

Уравнения, сформулированные Джеймсом Клерком Максвеллом, возникли на основе ряда важных экспериментальных открытий, которые были сделаны в начале XIX века. В 1820 году Ганс Христиан Эрстед обнаружил^[1], что пропускаемый через провод гальванический ток заставляет отклоняться магнитную стрелку компаса. Это открытие привлекло широкое внимание учёных того времени. В том же 1820 году Био и Савар экспериментально нашли выражение^[2] для порождаемой током магнитной индукции (закон Био — Савара), и Андре Мари Ампер обнаружил, что взаимодействие на расстоянии возникает также между двумя проводниками, по которым пропускается ток. Ампер ввёл термин «электродинамический» и выдвинул гипотезу, что природный магнетизм связан с существованием в магните круговых токов^[3].

Влияние тока на магнит, обнаруженное Эрстедом, привело Майкла Фарадея к идее о том, что должно существовать обратное влияние магнита на токи. После длительных экспериментов, в 1831 году, Фарадей открыл, что перемещающийся возле проводника магнит порождает в проводнике электрический ток. Это явление было названо электромагнитной индукцией. Фарадей ввёл понятие «поля сил» — некоторой среды, находящейся между зарядами и токами. Его рассуждения носили качественный характер, однако они оказали огромное влияние на исследования Максвелла.

После открытий Фарадея стало ясно, что старые модели электромагнетизма (Ампер, Пуассон и др.) неполны. Вскоре появилась теория Вебера, основанная на дальнодействии. Однако к этому моменту вся физика, кроме теории тяготения, имела дело только с близкодейственными силами (оптика, термодинамика, механика сплошных сред и др.). Гаусс, Риман и ряд других учёных высказывали догадки, что свет имеет электромагнитную природу, так что теория электромагнитных явлений тоже должна быть близкодейственной. Этот принцип стал существенной особенностью теории Максвелла.

В своём знаменитом «Трактате об электричестве и магнетизме» (1873) Максвелл писал^[4]:

Приступая к изучению труда Фарадея, я установил, что его метод понимания явлений был так же математическим, хотя и не представленным в форме обычных математических символов. Я также нашёл, что этот метод можно выразить в обычной математической форме и таким образом сравнить с методами профессиональных математиков.

Заменяя фарадеевский термин «поле сил» на понятие «напряжённость поля», Максвелл сделал его ключевым объектом своей теории^[5]:

Если мы примем эту среду в качестве гипотезы, я считаю, что она должна занимать выдающееся место в наших исследованиях, и что нам следовало бы попытаться сконструировать рациональное представление о всех деталях её действия, что и было моей постоянной целью в этом трактате.

Подобная электродинамическая среда явилась абсолютно новым понятием для ньютоновской физики. Последняя изучала взаимодействие между собой материальных тел. Максвелл же записал уравнения, которым должна подчиняться среда, определяющая взаимодействие зарядов и токов и существующая даже в их отсутствие.

Электрический ток создаёт магнитную индукцию (закон Ампера)

Анализируя известные эксперименты, Максвелл получил систему уравнений для электрического и магнитного полей. В 1855 году в своей самой первой статье «О фарадеевых силовых линиях»^[6] («On Faraday’s Lines of Force»^[7]) он впервые записал в дифференциальной форме систему уравнений электродинамики, но не вводя ещё ток смещения. Такая система уравнений описывала все известные к тому времени экспериментальные данные, но не позволяла связать между собой заряды и токи и предсказать электромагнитные волны^[8]. Впервые ток смещения был введён Максвеллом в работе «О физических силовых линиях»^[9] («On Physical Lines of Force»^[10]), состоящей из четырёх частей и опубликованной в 1861—1862 годах. Обобщая закон Ампера, Максвелл вводит ток смещения, вероятно, чтобы связать токи и заряды уравнением непрерывности, которое уже было известно для других физических величин^[8]. Следовательно, в этой статье фактически была завершена формулировка полной системы уравнений электродинамики. В статье 1864 года «Динамическая теория электромагнитного поля»^[11] («A dynamical theory of the electromagnetic field»^[12]) рассмотрена сформулированная ранее система уравнений из 20 скалярных уравнений для 20 скалярных неизвестных. В этой статье Максвелл впервые сформулировал понятие электромагнитного поля как физической реальности, имеющей собственную энергию и конечное время распространения, определяющее запаздывающий характер электромагнитного взаимодействия^[8].

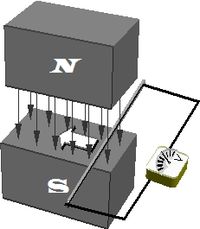
Переменный поток магнитного поля создаёт электрическое поле (закон Фарадея)

Оказалось, что не только ток, но и изменяющееся со временем электрическое поле (ток смещения) порождает магнитное поле. В свою очередь, в силу закона Фарадея, изменяющееся магнитное поле снова порождает электрическое. В результате, в пустом пространстве может распространяться электромагнитная волна. Из уравнений Максвелла следовало, что её скорость равна скорости света, поэтому Максвелл сделал вывод об электромагнитной природе света.

Часть физиков выступила против теории Максвелла (особенно много возражений вызвала концепция тока смещения). Гельмгольц предложил свою теорию, компромиссную по отношению к моделям Вебера и Максвелла, и поручил своему ученику Генриху Герцу провести её экспериментальную проверку. Однако опыты Герца однозначно подтвердили правоту Максвелла.

Максвелл не использовал векторных обозначений и записывал свои уравнения в достаточно громоздком компонентном виде. В своём трактате^[13] он, кроме того, частично использовал кватернионную формулировку. Современная форма уравнений Максвелла появилась около 1884 года после работ Хевисайда, Герца и Гиббса. Они не только переписали систему Максвелла в векторном виде, но и симметризовали её, переформулировав в терминах поля, избавившись от электрического и магнитного потенциалов, игравших в теории Максвелла существенную роль, поскольку полагали, что эти функции являются лишь ненужными вспомогательными математическими абстракциями^[14]. Интересно, что современная физика поддерживает Максвелла, но не разделяет негативное отношение его ранних последователей к потенциалам. Электромагнитный потенциал играет важную роль в квантовой физике и проявляется как физически измеряемая величина в некоторых экспериментах, например, в эффекте Ааронова — Бома^[15].

Система уравнений в формулировке Герца и Хевисайда некоторое время называлась уравнениями Герца — Хевисайда^[16]. Эйнштейн в классической статье «К электродинамике движущихся тел»^[17] назвал их уравнениями Максвелла — Герца. Иногда в литературе встречается также название уравнения Максвелла — Хевисайда^[18].

Уравнения Максвелла сыграли важную роль при возникновении специальной теории относительности (СТО). Джозеф Лармор (1900 год)^[19] и независимо от него Хенрик Лоренц (1904 год)^[20] нашли преобразования координат, времени и электромагнитных полей, которые оставляют уравнения Максвелла инвариантными при переходе от одной инерциальной системы отсчёта к другой. Эти преобразования отличались от преобразований Галилея классической механики и, следуя Анри Пуанкаре^[21], стали называться преобразованиями Лоренца. Они стали математическим фундаментом специальной теории относительности.

Распространение электромагнитных волн со скоростью света первоначально интерпретировалось как возмущения некоторой среды, так называемого эфира^[22]. Были предприняты многочисленные попытки (см. исторический обзор) обнаружить движение Земли относительно эфира, однако они неизменно давали отрицательный результат.^[23] Поэтому Анри Пуанкаре высказал гипотезу о принципиальной невозможности обнаружить подобное движение (принцип относительности). Ему же принадлежит постулат о независимости скорости света от скорости его источника и вывод (вместе с Лоренцем), исходя из сформулированного так принципа относительности, точного вида преобразований Лоренца (при этом были показаны и групповые свойства этих преобразований). Эти две гипотезы (постулата) легли и в основу статьи Альберта Эйнштейна (1905 год)^[17]. С их помощью он также вывел преобразования Лоренца и утвердил их общефизический смысл, особо подчеркнув возможность их применения для перехода из любой инерциальной системы отсчета в любую другую инерциальную. Эта работа фактически ознаменовала собой построение специальной теории относительности. В СТО преобразования Лоренца отражают общие свойства пространства и времени, а модель эфира оказывается ненужной. Электромагнитные поля являются самостоятельными объектами, существующими наравне с материальными частицами.

Классическая электродинамика, основанная на уравнениях Максвелла, лежит в основе многочисленных приложений электро- и радиотехники, СВЧ и оптики. До настоящего времени не было обнаружено ни одного эффекта, который потребовал бы видоизменения уравнений. Они оказываются применимы и в квантовой механике, когда рассматривается движение, например, заряженных частиц во внешних электромагнитных полях. Поэтому уравнения Максвелла являются основой микроскопического описания электромагнитных свойств вещества.

Уравнения Максвелла востребованы также в астрофизике и космологии, поскольку многие планеты и звезды обладают магнитным полем. Магнитное поле определяет, в частности, свойства таких объектов, как пульсары и квазары.

На современном уровне понимания все фундаментальные частицы являются квантовыми возбуждениями («квантами») различных полей. Например, фотон — это квант электромагнитного поля, а электрон — квант спинорного поля^[24]. Поэтому полевой подход, предложенный Фарадеем и существенно развитый Максвеллом, является основой современной физики фундаментальных частиц, в том числе её стандартной модели.

• Исторически несколько раньше он сыграл важную роль в появлении квантовой механики в формулировке Шрёдингера и вообще открытии квантовых уравнений, описывающих движение частиц, в том числе и релятивистских (уравнение Клейна — Гордона, уравнение Дирака), хотя первоначально аналогия с уравнениями Максвелла здесь виделась скорее лишь в общей идее, тогда как впоследствии оказалось, что она может быть понята как более конкретная и детальная (как это описано выше).

Также полевой подход, в целом восходящий к Фарадею и Максвеллу, стал центральным в теории гравитации (включая ОТО).