
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения в изотропных и однородных средах без дисперсииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В изотропных и однородных средах без дисперсии уравнения Максвелла принимают следующий вид:
В оптическом диапазоне частот вместо диэлектрической проницаемости Поскольку уравнения Максвелла в линейной среде являются линейными относительно полей Если распределения зарядов и токов При распространении электромагнитных полей в линейной среде в отсутствие зарядов и токов сумма любых частных решений уравнений будет также удовлетворять уравнениям Максвелла. Граничные условия Во многих случаях неоднородную среду можно представить в виде совокупности кусочно-непрерывных однородных областей, разделённых бесконечно тонкими границами. При этом можно решать уравнения Максвелла в каждой области, «сшивая» на границах получающиеся решения. В частности, при рассмотрении решения в конечном объёме необходимо учитывать условия на границах объёма с окружающим бесконечным пространством. Граничные условия получаются из уравнений Максвелла предельным переходом. Для этого проще всего воспользоваться уравнениями Максвелла в интегральной форме. Выбирая во второй паре уравнений контур интегрирования в виде прямоугольной рамки бесконечно малой высоты, пересекающей границу раздела двух сред, можно получить следующую связь между компонентами поля в двух областях, примыкающих к границе[37]:
где Аналогичным образом, выбирая область интегрирования в первой паре интегральных уравнений в виде цилиндра бесконечно малой высоты, пересекающего границу раздела так, что его образующие перпендикулярны границе раздела, можно получить:
где Эти граничные условия показывают непрерывность нормальной компоненты вектора магнитной индукции (нормальная компонента электрической индукции непрерывна только при отсутствии на границе поверхностных зарядов). Из уравнения непрерывности можно получить граничное условие для токов:
Важным частным случаем является граница раздела диэлектрика и идеального проводника. Поскольку идеальный проводник имеет бесконечную проводимость, электрическое поле внутри него равно нулю (иначе оно порождало бы бесконечную плотность тока). Тогда в общем случае переменных полей из уравнений Максвелла следует, что и магнитное поле в проводнике равно нулю. В результате тангенциальная компонента электрического и нормальная магнитного поля на границе с идеальным проводником равны нулю:
Законы сохранения Уравнения Максвелла содержат в себе законы сохранения заряда и энергии электромагнитного поля. Уравнение непрерывности для зарядов и токов (сохранение заряда) Источники полей (
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 428; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.239.63 (0.006 с.) |


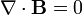
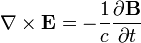


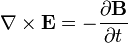

 используется показатель преломления
используется показатель преломления  (зависящий от длины волны), показывающий отличие скорости распространения монохроматической световой волны в среде от скорости света в вакууме. При этом в оптическом диапазоне диэлектрическая проницаемость обычно заметно меньше чем на низких частотах, а магнитная проницаемость большинства оптических сред практически равна единице. Показатель преломления большинства прозрачных материалов составляет от 1 до 2, достигая 5 у некоторых полупроводников[36]. В вакууме и диэлектрическая, и магнитная проницаемости равны единице:
(зависящий от длины волны), показывающий отличие скорости распространения монохроматической световой волны в среде от скорости света в вакууме. При этом в оптическом диапазоне диэлектрическая проницаемость обычно заметно меньше чем на низких частотах, а магнитная проницаемость большинства оптических сред практически равна единице. Показатель преломления большинства прозрачных материалов составляет от 1 до 2, достигая 5 у некоторых полупроводников[36]. В вакууме и диэлектрическая, и магнитная проницаемости равны единице:  .
. и свободных зарядов и токов
и свободных зарядов и токов  , справедлив принцип суперпозиции:
, справедлив принцип суперпозиции: создают электромагнитное поле с компонентами
создают электромагнитное поле с компонентами  , а другие распределения
, а другие распределения  создают, соответственно, поле
создают, соответственно, поле  , то суммарное поле, создаваемое источниками
, то суммарное поле, создаваемое источниками  , будет равно
, будет равно  .
.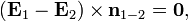

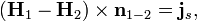
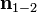 — единичный вектор нормали к поверхности, направленный из среды 1 в среду 2 и имеющий размерность, обратную длине,
— единичный вектор нормали к поверхности, направленный из среды 1 в среду 2 и имеющий размерность, обратную длине,  — плотность поверхностных свободных токов вдоль границы (то есть не включая связанных токов намагничивания, складывающихся на границе среды из микроскопических молекулярных и тому подобных токов). Первое граничное условие можно интерпретировать как непрерывность на границе областей тангенциальных компонент напряжённостей электрического поля (из второго следует, что тангенциальные компоненты напряжённости магнитного поля непрерывны только при отсутствии поверхностных токов на границе).
— плотность поверхностных свободных токов вдоль границы (то есть не включая связанных токов намагничивания, складывающихся на границе среды из микроскопических молекулярных и тому подобных токов). Первое граничное условие можно интерпретировать как непрерывность на границе областей тангенциальных компонент напряжённостей электрического поля (из второго следует, что тангенциальные компоненты напряжённости магнитного поля непрерывны только при отсутствии поверхностных токов на границе).


 — поверхностная плотность свободных зарядов (то есть не включающая в себя связанных зарядов, возникающих на границе среды вследствие диэлектрической поляризации самой среды).
— поверхностная плотность свободных зарядов (то есть не включающая в себя связанных зарядов, возникающих на границе среды вследствие диэлектрической поляризации самой среды).
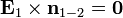





 ) не могут быть заданы произвольным образом. Применяя операцию дивергенции к четвёртому уравнению (закон Ампера — Максвелла) и используя первое уравнение (закон Гаусса), можно получить уравнение непрерывности для зарядов и токов:
) не могут быть заданы произвольным образом. Применяя операцию дивергенции к четвёртому уравнению (закон Ампера — Максвелла) и используя первое уравнение (закон Гаусса), можно получить уравнение непрерывности для зарядов и токов:



