
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наибольшее и наименьшее значения функции на отрезкеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Наибольшим значением функции на отрезке называется самое большое из всех ее значений на этом отрезке, а наименьшим – самое маленькое из всех ее значений. Рассмотрим функцию y = f (x) непрерывную на отрезке [ a, b ]. По теореме Вейерштрасса такая функция достигает своего наибольшего и наименьшего значений, либо на границе отрезка, либо внутри него. Если наибольшее или наименьшее значение функции достигается во внутренней точке отрезка, то это значение является максимумом или минимумом функции, то есть достигается в стационарных точках. Таким образом, получаем следующее правило нахождения наибольшего и наименьшего значений функции на отрезке[ a, b ]: 1.Найти все стационарные точки функции в интервале (a, b) и вычислить значения функции в них. 2.Вычислить значения функции на концах отрезка при x = a, x = b. 3.Из всех полученных значений выбрать наибольшее и наименьшее.
ВЫПУКЛОСТЬ ГРАФИКА ФУНКЦИИ. ТОЧКИ ПЕРЕГИБА
График функции На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c).
Рассмотрим достаточный признак, позволяющий установить, будет ли график функции в данном интервале выпуклым или вогнутым. Теорема 1. Пусть
Точка графика непрерывной функции, в которой изменяется выпуклость на вогнутость или наоборот, называется точкой перегиба. Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, т.к. с одной стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею. Определим достаточные условия того, что данная точка кривой является точкой перегиба. Теорема 2(достаточный признак точки перегиба). Пусть кривая определяется уравнением ►Пусть f ''(x) < 0 при x < x0 и f ''(x) > 0 при x > x0. Тогда при x < x0 кривая выпукла, а при x > x0 – вогнута. Следовательно, точка A, лежащая на кривой, с абсциссой x0 есть точка перегиба. Аналогично можно рассматривать второй случай, когда f ''(x) > 0 при x < x0 и f ''(x) < 0 при x > x0. ◄ Таким образом, точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует.
Заметим, что для непрерывных функций, которые являются дифференцируемыми не во всех точках, также используется понятие выпуклости кривой. Оно возникает, например, в математическом программировании. Здесь не может быть использовано определение, основанное на понятии касательной (касательной в этом случае может и не быть). Поэтому пользуются другим определением, основанным на понятии хорды. График функции (или сама функция) называется выпуклым (выпуклой), если каждая дуга кривой лежит не выше своей хорды. График функции (или сама функция) называется вогнутым (вогнутой), если каждая дуга кривой лежит не ниже своей хорды. В случае дифференцируемых функций определения, основанные на понятиях касательной и хорды, совпадают.
АСИМПТОТЫ ГРАФИКА ФУНКЦИИ
При исследовании функции важно установить форму ее графика при неограниченном удалении точки графика от начала координат. Особый интерес представляет случай, когда график функции при удалении его переменной точки в бесконечность неограниченно приближается к некоторой прямой.
Кривая, неограниченно приближаясь к своей асимптоте, может и пересекать ее, причем не в одной точке, как показано на приведенном графике функции Термин асимптота введен древнегреческим ученым Аполлонием Пергским при изучении гиперболы и происходит от греческого слова «асимтотос», означающего «несовпадающий». Хотя кривая может приближаться к своей асимптоте, оставаясь с одной стороны от нее или с разных сторон, бесконечное множество раз пересекая асимптоту и переходя с одной ее стороны на другую. Следует отметить, что не любая кривая имеет асимптоту. Исследование функций на наличие асимптот имеет большое значение и позволяет более точно определить характер функции и поведение графика кривой. Различают три вида асимптот: вертикальные, горизонтальные и наклонные. Вертикальные асимптоты Вертикальной асимптотой графика функции Вертикальные асимптоты следует искать в точках разрыва функции или на концах её области определения, если концы не равны График непрерывной на всей числовой прямой функции вертикальных асимптот не имеет. Горизонтальные асимптоты Если Наклонные асимптоты Поскольку асимптота – это прямая, то если кривая Теорема. Прямая y = kx + b служит наклонной асимптотой при x → ∞ для графика функции Замечание 1. Теорема показывает, что для нахождения наклонных асимптот достаточно найти два указанных предела. Причем, если хотя бы один из пределов не существует или обращается в бесконечность, то кривая наклонных асимптот не имеет. Замечание 2. Горизонтальная асимптота y = b является частным случаем наклонной y = kx + b при k = 0. Поэтому если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот. При отыскании асимптот, как правило, рассматривают лишь два случая: вертикальные и наклонные. Замечание 3. Пределы для отыскания k и b могут быть различны при x → +∞ и x → – ∞ и, следовательно, график функции может иметь две различные асимптоты при x → +∞ и x → –∞.
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1315; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.007 с.) |

 График функции
График функции  называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.
называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале. Прямая называется асимптотой графика функции
Прямая называется асимптотой графика функции  . Ее наклонная асимптота у = х.
. Ее наклонная асимптота у = х.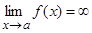 хотя бы при одном из условий x → а – 0 или x → а + 0.
хотя бы при одном из условий x → а – 0 или x → а + 0. .
. , то
, то  – горизонтальная асимптота кривой
– горизонтальная асимптота кривой 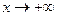 , левая при
, левая при 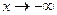 и двусторонняя, если пределы при
и двусторонняя, если пределы при  равны).
равны).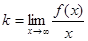 ,
,  .
.


