
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные теоремы дифференциального исчисленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теорема Ролля. Если функция f (x) непрерывна на отрезке [ a, b ], дифференцируема на интервале (а, b) и значения функции на концах отрезка равны f (a) = f (b), то на интервале (а, b) существует точка с, a < с < b, в которой производная функции f (x) равная нулю: f¢ (с) = 0.
Замечание. Если внутри [ a; b ] найдется хотя бы одна точка, в которой производная функции f (x) не существует, то утверждение теоремы может оказаться неверным. Теорема Ролля имеет несколько следствий: 1˚. Если функция f (x) на отрезке [ a, b ] удовлетворяет теореме Ролля, причем f (a) = f (b) = 0, то существует по крайней мере одна точка с, a < с < b, такая, что f ¢(с) = 0. Т.е. между двумя нулями функции найдется хотя бы одна точка, в которой производная функции равна нулю. 2˚. Если на рассматриваемом интервале (а, b) функция f (x) имеет производную (n – 1)-го порядка и n раз обращается в нуль, то существует, по крайней мере, одна точка интервала, в котором производная (n – 1)-го порядка равна нулю. Теорема Лагранжа (Жозеф Луи Лагранж (1736–1813) французский математик). Если функция f (x) непрерывна на отрезке [ a, b ] и дифференцируема во всех внутренних точках этого отрезка, то на интервале (а, b) найдется, по крайней мере, одна точка с (a < с < b), такая, что Это означает, что если на некотором промежутке выполняются условия теоремы, то отношение приращения функции к приращению аргумента на этом отрезке равно значению производной в некоторой промежуточной точке. Рассмотренная выше теорема Ролля является частным случаем теоремы Лагранжа.
Замечания. 1. Все условия теоремы существенны. 2. Выражение Теорема Коши (Коши (1789-1857) французский математик). Если f (x) и g (x) – две функции, непрерывные на [ a; b ] и дифференцируемые внутри него, причем g' (x) ≠ 0 при всех x Î (a; b), то внутри отрезка [ a; b ] найдется, хотя бы одна, точка c Î (a; b), что
Эта формула называется обобщенной формулой конечных приращений. Т.е. отношение приращений функций на данном отрезке равно отношению производных в точке с. Для доказательства этой теоремы на первый взгляд очень удобно воспользоваться теоремой Лагранжа. Записать формулу конечных разностей для каждой функции, а затем разделить их друг на друга. Однако, это представление ошибочно, т.к. точка с для каждой из функции в общем случае различна. Конечно, в некоторых частных случаях эта точка интервала может оказаться одинаковой для обеих функций, но это – очень редкое совпадение, а не правило, поэтому не может быть использовано для доказательства теоремы. Замечание. Рассмотренная выше теорема Лагранжа является частным случаем (при g (x) = x) теоремы Коши. Все эти теоремы применяются для доказательства самых разных теорем. Теорема Коши широко используется для раскрытия так называемых неопределенностей. Применение полученных результатов позволяет существенно упростить процесс вычисления пределов функций, что будет подробно рассмотрено ниже. ПРАВИЛО ЛОПИТАЛЯ Ранее мы познакомились с примерами нахождения пределов отношения двух бесконечно малых или бесконечно больших функций, то есть раскрытия неопределенностей вида 0/0 и ∞/∞. Сейчас рассмотрим новое правило раскрытия этих неопределенностей. Теорема (правило Лопиталя). Пусть функции f (x) и g (x) определены и дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a; g¢(x) ≠ 0 в этой окрестности и пусть Коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных. Замечание. Формула (1) справедлива только в том случае, если предел, стоящий справа, существует. Может случиться, что предел, стоящий слева существует, в то время как предел, стоящий в правой части равенства, не существует. Например, найти Если при решении примера после применения правила Лопиталя попытка вычислить предел опять приводит к неопределенности0/0 или ∞/∞, то правило Лопиталя может быть применено второй раз, третий и т.д. пока не будет получен результат. Это возможно только в том случае, если вновь полученные функции в свою очередь удовлетворяют требованиям теоремы Лопиталя.
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 743; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.007 с.) |

 Геометрический смысл теоремы Ролля состоит в том, что при выполнении условий теоремы на интервале (a, b) существует точка с такая, что в соответствующей точке кривой y = f (x) касательная параллельна оси О х. Таких точек на интервале может быть и несколько, но теорема утверждает существование, по крайней мере, одной такой точки.
Геометрический смысл теоремы Ролля состоит в том, что при выполнении условий теоремы на интервале (a, b) существует точка с такая, что в соответствующей точке кривой y = f (x) касательная параллельна оси О х. Таких точек на интервале может быть и несколько, но теорема утверждает существование, по крайней мере, одной такой точки. .
. Теорему Лагранжа геометрически можно пояснить так. Рассмотрим график функции y = f (x), удовлетворяющий условиям теоремы, и соединим концы графика на [ a; b ] хордой AB. Отношение
Теорему Лагранжа геометрически можно пояснить так. Рассмотрим график функции y = f (x), удовлетворяющий условиям теоремы, и соединим концы графика на [ a; b ] хордой AB. Отношение  равно угловому коэффициенту хорды АВ, а f '(c) есть угловой коэффициент касательной. Следовательно, теорема утверждает, что на графике функции y = f (x) найдется хотя бы одна точка, в которой касательная к графику параллельна хорде, соединяющей концы дуги.
равно угловому коэффициенту хорды АВ, а f '(c) есть угловой коэффициент касательной. Следовательно, теорема утверждает, что на графике функции y = f (x) найдется хотя бы одна точка, в которой касательная к графику параллельна хорде, соединяющей концы дуги. называется формулой Лагранжа или формулой конечных приращений.
называется формулой Лагранжа или формулой конечных приращений. .
. или
или  . Тогда предел отношения функций при х® а равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует
. Тогда предел отношения функций при х® а равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует 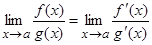 (1)
(1) . Этот предел существует
. Этот предел существует  . Но отношение производных (1 + cos x) / 1 = 1 + cos x при x → ∞ не стремится ни к какому пределу.
. Но отношение производных (1 + cos x) / 1 = 1 + cos x при x → ∞ не стремится ни к какому пределу.


