
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Множественная регрессия и корреляция. Оценка параметров регрессии.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Множественная регрессия – это уравнения связей с несколькими элеметно-зависимыми перемененными. У=f(x1,х2…..xn) У-завис.переменная.(результатив) Х- не завис.переменная(факторы) Для построения уравнения множественных регрессий часто используется след.функции: линейная-у=а+в1х1+в2х2+….врхр+Ɛ Степенная- у=а*х1в*хв2….хрвр*Ɛ Экспоненты – у=еа+в1х1+в2х2+….врхр+Ɛ Гипербола у= Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов. множественная корреляция - характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком, или, иначе, оценивает тесноту совместного влияния факторов на результат.
Множественная корреляция лежит в пределах от 0 до 1 и должно быть больше или равно мах парному индексу корреляции.
Оценка параметров уравнения регрессии осуществляется с помощью t-критерия Стьюдента. С этой целью по каждому из параметров определяется его стандартная ошибка: mb, ma и mr. Стандартная ошибка коэффициента регрессии определяется по формуле:
Величина стандартной ошибки совместно с t-распределением Стьюдента при n-2 степенях свободы применяется для проверки значимости коэффициента регрессии и для расчета его доверительного интервала.
Частные коэффициенты эластичности рассчитываются по формуле:
где
27.
которые показывают, на сколько процентов в среднем изменится результат, при изменении соответствующего фактора на 1%. Средние показатели эластичности можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат. Множественная регрессия. Индекс множественной корреляции для уравнений в естественной форме и в стандартизированном масштабе. Для построения уравнения множественных регрессий чаще используются след. функции: Вид множественной линейной модели регрессионного анализа: Y = b0 + b1xi1 +... + bjxij +... + bkxik + ei где ei - случайные ошибки наблюдения, независимые между собой, имеют нулевую среднюю и дисперсию s. Назначение множественной регрессии: анализ связи между несколькими независимыми переменными и зависимой переменной. Экономический смысл параметров множественной регрессии Коэффициент множественной регрессии bj показывает, на какую величину в среднем изменится результативный признак Y, если переменную Xj увеличить на единицу измерения, т. е. является нормативным коэффициентом. Значение индекса множественной корреляции лежит в пределах от (0 до 1).
Оценка статистической значимости Присутствия фактора в уравнении Множественной регрессии. Значимость уравнений множественной регрессии в целом оценивается с помощью критерия Фишера: F=R²/1-R² * n-m-1/m Если F табл< F ф то гипотезу о незначимости уравнения регрессии не отвергают. Если F табл> F ф,то выдвинутую гипотезу отвергают и принимают альтернативную гипотезу о статистической значимости уравнения регрессии. Оценка значимости коэффициентов чистой регрессии с помощью t-критерия Стьюдента сводится к вычислению значения:
Частный F критерий оценивает стат. Значимость присутствия каждого из факторов уравнений:
Если Fкр меньше табличного, то включение в модель данного фактора x1 после введения в нее фактора x2 нецелесообразно, и наоборот. Мультиколлинеарность факторов, их Проверка. Проверка мультиколлиниарности факторов проведена методом испытания гипотезы по независимым переменным. Гипотеза Н0: Det /R/=1. Доказано, что величина [n-1-1/Ϭ(2m+5)lg Det R] имеет приближенное расп-ие Х² с (1/2n(n-1)) степени свободы. Если фактическое значение Х² факт > Х² табл, то Н0 откл. Это означает, что Det /R/=(не равно)1. не диагональным ненулевым коэф. корреляции указывают на колиниарность факторов. Мультиколиниарность считается доказанной.
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 849; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |


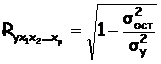 , где
, где 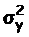 - общая дисперсия результативного признака;
- общая дисперсия результативного признака;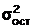 - остаточная дисперсия для уравнения у = f(x1,x2, …,xp).
- остаточная дисперсия для уравнения у = f(x1,x2, …,xp).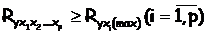
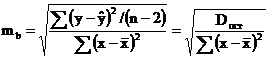

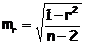

 ,
, - среднее значение фактора
- среднее значение фактора  ;
; 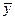 - среднее значение результата у. Частный коэффициент эластичности показывает, насколько процентов в среднем изменяется результату с увеличением фактора
- среднее значение результата у. Частный коэффициент эластичности показывает, насколько процентов в среднем изменяется результату с увеличением фактора 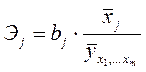 где
где 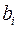 – коэффициент регрессии для фактора
– коэффициент регрессии для фактора 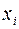 в уравнении множественной регрессии. Наряду с частными коэффициентами эластичности могут быть найдены средние по совокупности показатели эластичности:
в уравнении множественной регрессии. Наряду с частными коэффициентами эластичности могут быть найдены средние по совокупности показатели эластичности: ,
,


