
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Индентификация уравнений системы. Необходимое и достаточное условие индентифицируемости.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Индентификация-устан. между приведенным и структурной формой модели. С позиции идентифицируемости структурные модели можно подразделить на три вида: · идентифицируемые; · неидентифицируемые; · сверхидентифицируемые. Модель идентифицируема, если все ее структурные коэффициенты определяются однозначно, единственным образом, по коэффициентам приведенной формы модели, т.е. число параметров структурной модели равно числу параметров приведенной формы модели. Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели. Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить два и более значений одного структурного коэффициента. Необходимое условие идентифицируемости: D + 1 = H – уравнение идентифицируемо; D + 1 < H – уравнение неидентифицируемо; D + 1 > H – уравнение сверхидентифицируемо, где H – число эндогенных переменных в уравнении, D – число экзогенных переменных, которые содержатся в системе, но не входят в данное уравнение. Достаточное условие идентифицируемости: Уравнение идентифицируемо, если по отсутствующим в нем переменным можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без единицы. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно из уравнений неидентифицируемо, то и вся модель считается неидентифицируемой. 27. Временные ряды в эконометрических исследованиях. Аддитивные и мультипликативные модели. 1. Тенденции, характеризующей общее направление динамики изучаемого явления. Аналитически тенденция выражается некоторой функцией времени, называемой трендом (Т). 2. Циклической или периодической составляющей, характеризующей циклические или периодические колебания изучаемого явления. Колебания представляют собой отклонения фактических уровней ряда от тренда. Объем продаж некоторых товаров подвержен сезонным колебаниям. Сезонные колебания (S) – периодические колебания, которые имеют определенный и постоянный период равный годовому промежутку. 3. Случайной составляющей, которая является результатом воздействия множества случайных факторов (Е). Тогда уровень ряда можно представить как функцию от этих составляющих (компонентов): Y =f(T, S, E).
29. Моделирование тенденции временного ряда. Пусть имеются следующие фактические уровни ряда: у1, у2,..., уn. Характер изменения этих уровней, то есть движения динамического ряда, может быть различным. Поскольку зависимость от времени может принимать разные формы, для ее формализации можно использовать различные виды функций. Для построения трендов чаще всего применяются следующие функции: · линейный тренд: yt = a0 + a1t; yt = a0 + a1t + a2 t 2 +... +ak t k . Аналитическое выравнивание есть не что иное, как удобный способ описания эмпирических данных. Общие соображения при выборе типа линии, по которой производится аналитическое выравнивание, могут быть сведены к следующим: 1) Если абсолютные приросты уровней ряда по своей величине колеблются около постоянной величины, то математической функцией, уравнение которой можно принять за основу аналитического выравнивания, следует считать прямую линию: yt = a0 + a1 t, где yt считается как у, выровненный по t. 2) Если приросты приростов уровней, то есть ускорения, колеблются около постоянной величины, то за основу аналитического выравнивания, следует принять параболу второго порядка: yt = a0 + a1 t + a2 t 2. Показатели а0, а1 и а2 представляют собой в каждом отдельном случае выравнивания постоянные величины, называемые параметрами: а0 -начальный уровень; а1 - начальная скорость ряда и а2 - ускорение или вторая скорость. 3) Если уровни изменяются с приблизительно постоянным относительным приростом, то выравнивание производится по показательной (экспонентной функции): yt = a0 a1t. В этих же целях можно использовать и коэффициенты автокорреляции уровней ряда. Тип тенденции можно определить путём сравнения коэффициентов автокорреляции первого порядка, рассчитанным по исходным и преобразованным уровням ряда. Если временной ряд имеет линейную тенденцию, то его соседние уровни yt и y t -1 тесно коррелируют. В этом случае коэффициент автокорреляции первого порядка уровней исходного ряда должен быть высоким. Если временной ряд содержит нелинейную тенденцию, например, в форме экспоненты, то коэффициент автокорреляции первого порядка по логарифмам уровней исходного ряда будет выше, чем соответствующий коэффициент, рассчитанный по уровням ряда. Чем сильнее выражена нелинейная тенденция в изучаемом временном ряде, тем в большей степени будут различаться значения указанных коэффициентов.
Для дальнейшего анализа используют не исходные данные, а отклонение от тренда. 2. Метод последовательных разностей. (формула)
31. Автокорреляция и авторегрессия временного ряда. Количественно её можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени. Определим коэффициент между рядами yt и yt-1. Коэф. Автокорреляции.
Число периодов по которым определяется коэффициент автокорреляции, называют лаг автокорреляции. С ростом лага число пар значений по которым рассчитывается коэффициент автокорреляции уменьшается. Считается что лаг должен определяться отношением n/4-количество наблюдений деленных на 4. Последовательность коэффициентов автокорреляции уровней первого, второго и т. д. Порядков называют автокорреляционной функцией временного ряда. График зависимости её значений от величины лага (порядка коэффициента корреляции) называется коррелограммой. Авторегрессия – это статистический метод определения потенциальной потери капитала или его дохода. В данном способе для предположения последующих значений используются предыдущие значения временных рядов. Прогнозы, сделанные по методам авторегрессии, считаются одними из наиболее точных статистических прогнозов. Это объясняется тем, что моделями авторегрессии великолепно описывается большое количество самых разных экономических показателей. По большому счету формулу автокорреляционной функции, которая применяется в авторегрессивных моделях, использовать нельзя – она применима исключительно к стационарным рядам
где сигма - это случайная величина, Х - вектор имеющихся отсчётов первых разностей прогнозируемого ВР, а Y(i)- коэффициенты авторегрессии, на вид которых имеются ограничения. Для вычисления коэффициентов авторегрессии необходимо решить систему линейных удобрений энного порядка, состоящую из значений автокорреляционной функции для ряда первых разностей. После нахождения разности Х(i+1) не сложно составить прогноз для исходного ВР, а именно: Y(i+1)=Y(i)+X(i+1).
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 656; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.26.184 (0.008 с.) |

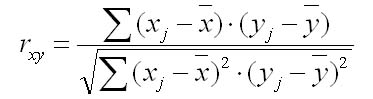
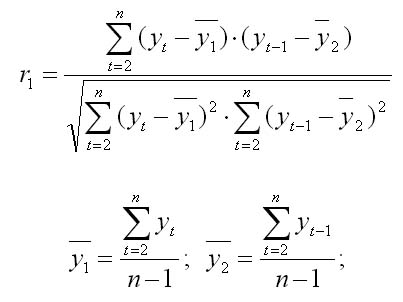
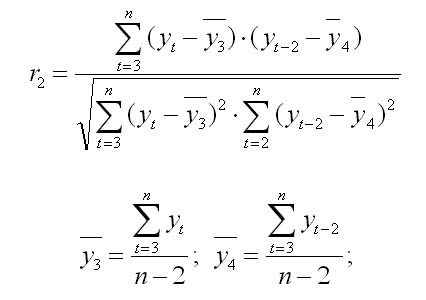
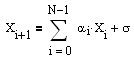 (рис. 1 - авторегрессивная модель энного порядка)
(рис. 1 - авторегрессивная модель энного порядка)


