
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 7 Линейная парная регрессия , линейный коэффициент парной корреляцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Линейная парная регрессия-УРАВНЕНИЕ связи 2-х переменных у=f^(x), Где у-зависимая переменная, х- независимая, объясняющая. Различают линейные и нелинейные регрессии. Линейная имеет вид e=a+bx+E. Линейный коэффициент парной корреляции (р) определяется по формуле:
где х, у — значения факторного и результативного показателей соответственно; х, у — средние значения соответствующих показателей; σ X, σ Y - средние квадратические отклонения (стандартные отклонения показателей х и у);
n — количество наблюдений в совокупности. Значение коэффициента парной корреляции изменяется в пределах от -1 до +1. Знак «+» означает наличие прямой связи между показателями. Знак «-» — наличие обратной связи. Значение коэффициента от 0 до 1 характеризует степень приближения корреляционной зависимости между показателями и к функциональной. При р = 1 между показателями существует функциональная связь. При р = 0 линейная связь отсутствует. В целях упрощения расчетов на практике применяются и другие формулы коэффициента парной корреляции, представляющие собой некоторые преобразования исходной формулы. Вопрос 8 Коэффициент детерминации и его характеристика Коэффициент детерминации ( Формула для вычисления коэффициента детерминации:
где Также это квадрат корреляции Пирсона между двумя переменными. Он выражает количество дисперсии, общей между двумя переменными. Коэффициент принимает значения из интервала В случае парной линейной регрессионной модели коэффициент детерминации равен квадрату коэффициента корреляции, то есть 9. Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических: Ā= Допустимый предел значимости не более 8-10%. Критерий Фишера. Оценка качества уравнения регрессии. Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью F-критерия Фишера:
Dост - остаточная сумма квадратов на одну степень свободы; R2 - коэффициент (индекс) множественной детерминации; m – число параметров при переменных х n – число наблюдений. Частный F-критерий построен на сравнении прироста факторной дисперсии, обусловленного влиянием дополнительно включенного фактора, с остаточной дисперсией на одну степень свободы по регрессионной модели в целом. Оценивание качества модели по F -критерию Фишера состоит в проверке гипотезы H0 о статистической незначимости уравнения регрессии. Для этого наблюдаемое значение Если Fнабл > Fкр, то признается статистическая значимость и надежность уравнения регрессии. Если Fнабл < Fкр, то признается статистическая незначимость и ненадежность уравнения регрессии. Оценка статистической значимости коэффициентов регрессии и корреляции. Для оценки стат-х значимости коэф. Корреляции рассчитывается t-критерий стюдента и доверительный интервалы каждого показателя. Для оценки значимости коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т.е. определяется фактическое значение t-критерия Стьюдента:
которое затем сравнивается с табличным значением при определенном уровне значимости a и числе степеней свободы n-2. Если tфакт>tтабл, то делается вывод о значимости параметра. Оценка значимости коэф.регрессии и кореляции с помощью t-критерия стюдента проводится путем сопоставления и значений велечиной случайной ошибки.
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1156; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |



 )— это квадрат множественного коэффициента корреляции. Он показывает, какая доля дисперсии результативного признака объясняется влиянием независимых переменных.
)— это квадрат множественного коэффициента корреляции. Он показывает, какая доля дисперсии результативного признака объясняется влиянием независимых переменных.
 — выборочные данные, а
— выборочные данные, а  — соответствующие им значения модели.
— соответствующие им значения модели. . Чем ближе значение к 1 тем ближе модель к эмпирическим наблюдениям.
. Чем ближе значение к 1 тем ближе модель к эмпирическим наблюдениям. .
. ∑
∑  *100%
*100% , где Dфакт - факторная сумма квадратов на одну степень свободы;
, где Dфакт - факторная сумма квадратов на одну степень свободы; -критерия Фишера (2.13) сравнивается с критическим (табличным) значением
-критерия Фишера (2.13) сравнивается с критическим (табличным) значением  при уровне значимости
при уровне значимости  и степенях свободы
и степенях свободы  и
и  . Уровень значимости α – вероятность отвергнуть гипотезу при условии что она верна. Обычно принимается равной 0,05 или 0,01.
. Уровень значимости α – вероятность отвергнуть гипотезу при условии что она верна. Обычно принимается равной 0,05 или 0,01. , причем
, причем 

 , причем
, причем 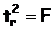 , т.е.
, т.е. 



