Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение точечных оценок параметров совместного распределения признаков. Формирование выборочной корреляционной матрицыСодержание книги
Поиск на нашем сайте
Исходные данные
I. Корреляционный анализ Постановка задачи Требуется на основании указанных в приведенной таблице статистических данных для n=14 стран, отобранных случайным образом, исследовать стохастическую зависимость между социальными показателями X, Y, Z, полагая, что их совместное распределение подчинено трехмерному нормальному закону. К вопросам анализа относятся: - оценка тесноты связи между произвольными двумя наблюдаемыми признаками при фиксировании или исключении влияния третьего признака; - оценка тесноты связи каждого из рассматриваемых признаков с совокупностью остальных признаков; - проверка значимости коэффициентов связи; - интервальное оценивание коэффициентов связи. - построение модели корреляционной зависимости между признаками. Определение точечных оценок параметров совместного распределения признаков. Формирование выборочной корреляционной матрицы Признаки X, Y, Z образуют трехмерную нормально распределенную генеральную совокупность, которая определяется девятью параметрами: • тремя математическими ожиданиями MX, MY, MZ; • тремя дисперсиями DX, DY, DZ; • тремя парными коэффициентами корреляции ρxy; ρxz; ρyz. Выборочные средние
Выборочные средние квадратические отклонения
Выборочные парные коэффициенты корреляции
Матрица выборочных парных коэффициентов корреляции
Исследование парных коэффициентов корреляции Парный коэффициент корреляции численно характеризует тесноту связи между произвольными двумя признаками, выбранными из совокупности рассматриваемых показателей, на фоне влияния третьего показателя, введенного в корреляционный анализ.
Проверка значимости парных коэффициентов корреляции (при уровне значимости применяемого статистического критерия α= 0,05) Проверяемые гипотезы:
Наблюдаемые значения статистики критерия:
Нахождение tкр - граничного значения области отвержения гипотезы Способы: Ø или из статистической таблицы 2 (Значения функции
Ø или с помощью статистической функции Microsoft Excel СТЬЮДРАСПОБР (вероятность; степени_свободы): tкр = СТЬЮДРАСПОБР (α; n-2 ). В данном случае tкр=2,1788. Условие отвержения гипотезы
Результаты проверки гипотез: v гипотеза H0: ρxy=0 не отвергается, парный коэффициент корреляции между X и Y не значим; v гипотеза H0: ρxz=0 не отвергается, парный коэффициент корреляции между X и Z не значим; v гипотеза H0: ρyz=0 отвергается, парный коэффициент корреляции между Y и Z значим. Вывод Между признаками Y, Z существует значимая обратная умеренная корреляционная зависимость. Вывод Доверительный интервал для парного коэффициента корреляции ρyz не содержит нуля, что подтверждает значимость данного коэффициента. Исследование частных коэффициентов корреляции Частный коэффициент корреляции позволяет численно оценить тесноту связи между любыми двумя признаками из числа рассматриваемых показателей, исключая при анализе их зависимости (в случае трехмерной корреляционной модели) влияние на эту зависимость третьего показателя. Выборочные частные коэффициенты корреляции
Условие отвержения гипотезы о незначимости частного коэффициента корреляции
Результаты проверки гипотез: v гипотеза H0: ρxy/z =0 не отвергается, частный коэффициент корреляции между X и Y не значим; v гипотеза H0: ρxz/y=0 отвергается, частный коэффициент корреляции между X и Z значим; v гипотеза H0: ρyz/x=0 отвергается, частный коэффициент корреляции между Y и Z значим. Вывод Доверительные интервалы для частных коэффициентов корреляции ρxz/y, ρyz/x не содержат нуля, что дополнительно подтверждает значимость этих коэффициентов.
Общий вывод Результаты выполненного корреляционного анализа показывают, что признак Z имеет статистически значимую умеренную связь как с двумерным массивом признаков X, Y, так и с каждым из этих признаков в отдельности, что дает основание для перехода ко второму этапу статистического исследования - построению регрессионной модели, т.е. выявлению той конкретной математической зависимости переменной Z от переменных X, Y, которой наилучшим, в определенном смысле этого слова, образом отвечают имеющиеся статистические данные. II. Регрессионный анализ Постановка задачи Требуется по указанным выше статистическим данным n=14 стран произвести регрессионный анализ зависимости уровня смертности от средней продолжительность жизни женщин и уровня рождаемости. Исходные данные
I. Корреляционный анализ Постановка задачи Требуется на основании указанных в приведенной таблице статистических данных для n=14 стран, отобранных случайным образом, исследовать стохастическую зависимость между социальными показателями X, Y, Z, полагая, что их совместное распределение подчинено трехмерному нормальному закону. К вопросам анализа относятся: - оценка тесноты связи между произвольными двумя наблюдаемыми признаками при фиксировании или исключении влияния третьего признака; - оценка тесноты связи каждого из рассматриваемых признаков с совокупностью остальных признаков; - проверка значимости коэффициентов связи; - интервальное оценивание коэффициентов связи. - построение модели корреляционной зависимости между признаками. Определение точечных оценок параметров совместного распределения признаков. Формирование выборочной корреляционной матрицы Признаки X, Y, Z образуют трехмерную нормально распределенную генеральную совокупность, которая определяется девятью параметрами: • тремя математическими ожиданиями MX, MY, MZ; • тремя дисперсиями DX, DY, DZ; • тремя парными коэффициентами корреляции ρxy; ρxz; ρyz. Выборочные средние
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 261; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.111.28 (0.011 с.) |

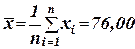


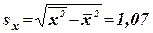

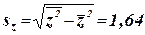





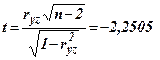
 , где случайная величина Т распределена по закону Стьюдента с числом степеней свободы, равным ν) на основании уравнения:
, где случайная величина Т распределена по закону Стьюдента с числом степеней свободы, равным ν) на основании уравнения: ,
, .
. ;
; ;
;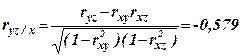 .
.