
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частные коэффициенты корреляции.Содержание книги
Поиск на нашем сайте
Частные коэффициенты корреляции. Частные коэффициенты (индексы) корреляции характеризуют тесноту связи между двумя признаками при исключении влияния третьего признака. Эти показатели представляют собой отношение сокращения остаточной дисперсии за счет включения доп. факторов. Если рассматриваемая регрессия с числом факторов Р, то возможны коэффициенты корреляции первого, второго и т.д. Р-1 порядков, т.е. ryx1.x2= корень квадр из(1-(1-R2yx1x2)/(1-r2yx2), ryx2.x1= корень квадр из(1-(1-R2yx1x2)/(1-r2yx1). Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается. Коэффициенты множественной корреляции, свойства коэффициента. Показатели множественной корреляции характеризуют тесноту связи, рассматриваемого набора фактора с исследуемым признаком, т.е. оценивает тесноту связи совместного влияния фактора на результат.
Свойства: 1. Изменяется в пределах [0;1],не используется для определения направленности связи. 2. Чем ближе к 1, тем теснее связь результативного признака со всем набором исследуемых факторов; Если значение близко к 0, то взаимосвязь слабая. 3. Величина коэф-та множественной корреляции должна быть ≥ максимальному парному индексу корреляции. 4. Добавление в уравнение множественной регрессии новую факторную переменную увеличивает значение множественного коэффициента корреляции. Оценка параметров уравнения множественной регрессии (Дисперсионный анализ). Оценка значимости уравнения регрессии в целом дается с помощью критерия Фишера. Перед расчетом критерия проводится дисперсионный анализ. 1.Выдвигаем нулевую гипотезу о статистической незначимости коэффициента регрессии и, следовательно, уравнения в целом: 2.Строим схему дисперсионного анализа. Рассчитываем среднеквадратическое отклонение (СКО):
3.Определяем наблюдаемое значения F- критерия:
Определяем табличное значение F- критерия:
4.Сопоставляем наблюдаемое и табличное значение, записываем вывод: Fфакт > Fтабл, то нулевая гипотеза отклоняется и делается вывод о том, что уравнение регрессии статистически значимо. Fфакт < Fтабл, то нулевая гипотеза не отклоняется и делается вывод о том, что уравнение регрессии статистически незначимо.
Частный F-критерий Фишера. С помощью F-критерия Фишера опред-ся значимость уравнения множеств регрессии в целом. Позволяет оценить целесообразность включения в уравнение множественной регрессии фактора х1 после х2, х2 после х1.
R 2yx1...xm -коэффициент множественной детерминации для регрессии с полным набором факторов. R2yx1...xi-1; xi+1...xm -для ур-ия множеств-й регрессии без включения в модель фактора xi. Частный F критерий построен на сравнении прироста факторной дисперсии, обусловленного влиянием дополнительно включенного фактора, с остаточной дисперсией на одну степень свободы по регрессионной модели в целом. Если Fxi>Fтабл при α=0,05 (заданном), то включение xi-го фактора статистически оправдано. Если Fxi<Fтабл – то не оправдано. С помощью частного F-критерия можно проверить значимость всех коэф-ов регрессии, предлагая, что каждый соотв-щий фактор xi вводился в ур-ие множ-й регр последним.
Оценка параметров уравнения множественной регрессии (по t-критерию Стьюдента). 1.Выдвигаем нулевую гипотезу о статистической незначимости коэффициентов чистой регрессии: 2. Наблюдаемое значение критерия:
3.Стандартная ошибка коэффициента:
4.Табличное значение t- критерия, 5. Сопоставляем наблюдаемое и табличное значение, записываем вывод:
Предпосылки МНК. После построения уравнения множественной регрессии проводится проверка наличия у оценок (y=a+b1x1+b2x2+…+bmxm+E) тех свойств, которые предполагаются при МНК. Это связано с тем, что оценки параметров для уравнения регрессии должны отвечать определенным критериям, а именно: д.б. эффективными, несмещенными, состоятельными. Несмещённость оценки означает, что математическое ожидание остатков равно нулю. Оценка считается эффективной, если она характеризуется наименьшей дисперсией. Состоятельность оценок характеризует увеличение их точности с увеличением объема выборки.
Условия, необходимые для получения оценок удовлетворяет этим 3 критериям представляет собой предпосылки МНК: 1. случайный характер остатка (строится график зависимости остатков Ei от теоретических значений результативного признака). 2. нулевая средняя величина остатков, не зависящая от Xi (сумма разностей фактических и теоретических значений равна нулю). 3. гомоскедастичность – дисперсия каждого отклонения одинаково для всех факторов. 4. отсутствие автокорреляции Еi распределены независимо друг от друга (наличие корреляции между остатками текущих и предыдущих наблюдений). 5. остатки подчиняются нормативному закону (корреляция между остатками текущего и предыдущего значения).
Частные коэффициенты корреляции. Частные коэффициенты (индексы) корреляции характеризуют тесноту связи между двумя признаками при исключении влияния третьего признака. Эти показатели представляют собой отношение сокращения остаточной дисперсии за счет включения доп. факторов. Если рассматриваемая регрессия с числом факторов Р, то возможны коэффициенты корреляции первого, второго и т.д. Р-1 порядков, т.е. ryx1.x2= корень квадр из(1-(1-R2yx1x2)/(1-r2yx2), ryx2.x1= корень квадр из(1-(1-R2yx1x2)/(1-r2yx1). Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается.
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 505; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.137.162 (0.008 с.) |

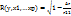 , r – номера признака, связь м/у которыми оценивается этим коэф-ом корреляции.
, r – номера признака, связь м/у которыми оценивается этим коэф-ом корреляции. .
. ;
;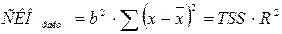 ;
;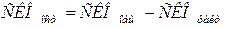 .
. .
.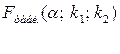
 ;
; .
.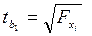
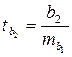 .
.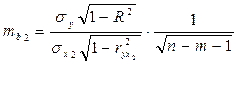 .
.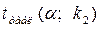 .
.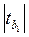 и
и  > tтабл, то нулевая гипотеза отклоняется и делается вывод о том, что коэффициенты уравнения статистически значимы.
> tтабл, то нулевая гипотеза отклоняется и делается вывод о том, что коэффициенты уравнения статистически значимы.


