
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предпосылки мнк: гомо и гетероскедастичности.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Условия необходимые для получения свойств оценок уравнения регрессии: 1) Случайный характер остатка. Для определения данной предпосылки строится график зависимости остатков от расчётных значений результативных переменных, если график остатков образует горизонтальную линию, то предпосылка считается оправданной. 2) Нулевая средняя величина остатка независящая от переменной X. Для определения строится график зависимости остатков, но по оси X будет обозначаться факторная переменная. Данное условие будет выполняться для линейных моделей и нелинейных относительно включённых в них переменных. Если график значений также образует горизонтальную линию, то остатки будут независимы от переменной X. Если будет формироваться, какая либо зависимость то данная предпосылка невыполнима. 3) Гомоскедастичность (а=в=с): определение, графическое изображение, последствия гетероскедастичности, и методы определения гетероскедастичности. Дисперсия остатков постоянна, это означает, что для каждого значения фактора X остатки имеют одинаковую дисперсию, если эта предпосылка не выполняется, то имеет место гетероскедастичности(а>в>с). Последствия гетероскедастичности остатка: 1) Для оценок регрессии не выполняется условие эффективности. 2) Появляется возможность неверного вычисления стандартных ошибок коэффициентов. 4)Отсутствие автокорреляции остатков. Автокорреляция - корреляция между остатками текущего и предыдущего значения. Автокорреляция определяется критерием Дарбина-Уотсона. Если эти предпосылки не соблюдаются необходимо: 1) Проектировать модель, то есть изменить её спецификацию. 2) Изменить состав факторной переменной, 3) Преобразовать исходные данные. Метод определения гетероскедастичности. Тест Глейзера (тест ранговой корреляции Спирмена). Этапы теста: 1) Для построенной модели определяются остатки, полученные остатки возводятся в квадрат. 2) Рассчитывается коэффициент ранговой корреляции: где d – ‘это разность между r(x) и r(e), а n – количество переменных. Коэффициент Спирмена позволяет определить зависимость между качественными и количественными признаками, квадратом остатков и факторной переменной соответственно. 3) Переменная x ранжируется по возрастанию, её ранги будут обозначаться как r(x), далее определяются ранги остатков, которые обозначаются как r(e).
4) Значимость коэффициента Cпирмена определяется t-критерием Стьюдента.
Выдвигается нулевая гипотеза: Вывод: если t набл > t табл., то нулевая гипотеза откланяется, следовательно, присутствует гетероскедастичность. если t набл < t табл., то нулевая гипотеза не откланяется, следовательно, присутствует гомоскедастичность.
Метод определения гетероскедастичности. Тест Голфелда-Кванта. Все наблюдения упорядочиваются по величине х. Выборка делится на 3 части, где 1 и 3 части обязательно равны; разность м/у 1 и 2 частью также как 2 и 3 частью не равна 0, но при этом незначительна. 1-3 обозначаются К. Для каждой выборки опр. своя сумма квадратов отклонений: Проверка осуществляется по F-критерию:
Вывод: если F набл > F табл., то нулевая гипотеза откланяется, следовательно, присутствует гетероскедастичность. если F набл < F табл., то нулевая гипотеза не откланяется, следовательно, присутствует гомоскедастичность.
Предпосылки МНК. После построения уравнения множественной регрессии проводится проверка наличия у оценок (y=a+b1x1+b2x2+…+bmxm+E) тех свойств, которые предполагаются при МНК. Это связано с тем, что оценки параметров для уравнения регрессии должны отвечать определенным критериям, а именно: д.б. эффективными, несмещенными, состоятельными. Несмещённость оценки означает, что математическое ожидание остатков равно нулю. Оценка считается эффективной, если она характеризуется наименьшей дисперсией. Состоятельность оценок характеризует увеличение их точности с увеличением объема выборки. Условия, необходимые для получения оценок удовлетворяет этим 3 критериям представляет собой предпосылки МНК: 1. случайный характер остатка (строится график зависимости остатков Ei от теоретических значений результативного признака). 2. нулевая средняя величина остатков, не зависящая от Xi (сумма разностей фактических и теоретических значений равна нулю). 3. гомоскедастичность – дисперсия каждого отклонения одинаково для всех факторов. 4. отсутствие автокорреляции Еi распределены независимо друг от друга (наличие корреляции между остатками текущих и предыдущих наблюдений).
5. остатки подчиняются нормативному закону (корреляция между остатками текущего и предыдущего значения).
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 745; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.170.76 (0.007 с.) |

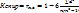
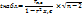
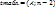

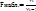 , Fтабл.=(γ; k-m-1; k-m-1)
, Fтабл.=(γ; k-m-1; k-m-1)


