
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Результаты обследования безработного населения областиСодержание книги
Поиск на нашем сайте
Рассчитаем среднюю из внутригрупповых дисперсий:
Определим среднюю и предельную ошибки выборки (с вероятностью 0,954):
Рассчитаем выборочную среднюю:
В результате проведенных расчетов с вероятностью 0,954 можно сделать вывод, что среднее число недель, затрачиваемых на поиск работы, в целом по области находится в пределах: 11,0 - 0.34 < х ¯ < 11,0 + 0,34. При определении необходимого объема типической выборки в рассмотренных выше формулах (7.6) и (7.7) общую дисперсию наблюдаемого признака необходимо заменить на среднюю из внутригрупповых дисперсий. Тогда данные формулы примут следующий вид:
Предположим, в рассмотренном выше примере нам необходимо определить среднее число недель, затрачиваемых на поиск работы, с предельной ошибкой ± 1 неделя. Учитывая величину полученной ранее средней из внутригрупповых дисперсий, определим необходимый объем типической выборки при условии бесповторного отбора:
Таким образом мы получили, что при заданных условиях для достижения требуемой точности достаточно обследовать выборочным методом всего 186 чел. Распределим эту численность на три района рассматриваемой области пропорционально их размерам по числу зарегистрированных безработных:
Расчеты показывают, что в районе А необходимо обследовать 61 чел., в районе Б -100 чел., и в районе В - 25 чел. Мы рассмотрели типический отбор, пропорциональный объему типических групп. Второй вариант формирования типической выборки заключается в отборе единиц, пропорциональном вариации признака в типических группах. Логика такого отбора заключается в следующем: если внутри какой-либо типической группы наблюдаемый признак варьирует слабо, то для определения границ генеральных характеристик из данной группы достаточно обследовать относительно небольшое число единиц; при сильной же вариации признака объем выборки должен быть соответственно увеличен.
Серийная выборка Сущность серийной выборки заключается в собственно-случайном либо механическом отборе групп единиц (серий), внутри которых производится сплошное обследование. Единицей отбора при этой выборке является группа или серия, а не отдельная единица генеральной совокупности, как это имело место в рассматриваемых ранее выборках. Данный способ отбора удобен в тех случаях, когда единицы генеральной совокупности изначально объединены в небольшие более или менее равновеликие группы или серии. В качестве таких серий могут выступать упаковки с определенным количеством готовой продукции, партии товара, студенческие группы, бригады и другие подобные объединения. В большинстве случаев серийная выборка имеет не столько методологические, сколько организационные преимуществами перед другими способами формирования выборочном совокупности. Например, в Великобритании серийный отбор используется в обследованиях населения, когда серией являются домохозяйства, объединенные общим почтовым индексом. В случайном порядке производится выборка индексов и под обследование попадают все домохозяйства, имеющие индекс попавших в выборочную совокупность матовых отделений. В связи с тем, что при серийном отборе внутри отобранных групп обследуются все исключения единицы, внутригрупповая вариация признака не отразится на ошибках Порочного наблюдения. В то же время, обследуются не все группы, а только попавшие в выборку. Следовательно на ошибках получаемых характеристик будут отражаться различия между группами, которые определяются межгрупповой дисперсией. Поэтому средняяошибка серийной выборки определяется по формулам:
где: r - число отобранных серий; R - общее число серий. Межгрупповую дисперсию при равновеликих группах вычисляют следующим образом:
где: xi - средняя i-й серии; x - общая средняя по всей выборочной совокупности. Рассмотрим следующий пример. Предположим, партия готовой продукции предприятия упакована в 160 ящиков по 25 изделий в каждом. В целях контроля соблюдения параметров технологического процесса проведена 5%-иая серийная выборка, в ходе которой отбирался каждый 20-й ящик. Все изделия, находящиеся в отобранных ящиках были подвергнуты сплошному обследованию, заключающемуся в определении их точного веса. Полученные результаты представлены в следующей таблице: Таблица 7.4.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 323; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.169.169 (0.006 с.) |


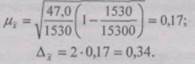

 (повторный отбор) (7.11.)
(повторный отбор) (7.11.) (бесповторный отбор) (7.12.)
(бесповторный отбор) (7.12.)
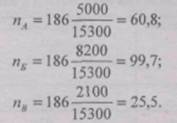
 (повторный отбор), (7.13.)
(повторный отбор), (7.13.) (бесповторный отбор), (7.14.)
(бесповторный отбор), (7.14.) (7.15.)
(7.15.)


