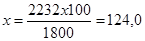Абсолютные величины, их применение в медицине

Абсолютная величина – это величина, характеризующая размах или единичность явления.

Из определения вытекают случаи применения абсолютных величин в медицине и здравоохранении. Абсолютные величины – это, например, численность населения, число лечебно-профилактических учреждений, число врачей, число инфекционных заболеваний, число больных и вирусоносителей СПИД и т.д.

Сравнивая размеры явлений или изучения изменение явлений во времени, следует абсолютные числа, выражающие эти размеры, привести к одному знаменателю, чаще всего – численность населения.

 

Относительные величины, их виды, методика расчета,

Применение в здравоохранении

Относительные величины (показатели, коэффициенты) – это величины, полученные путем отношения двух абсолютных величин, выраженных через третью абсолютную величину.

Виды относительных величин:

1. Экстенсивный показатель;

2. Интенсивный показатель;

3. Показатель соотношения;

4. Показатель наглядности.

Экстенсивный показатель (показатель распределения, структуры, состава явления, удельного веса) – показатель структуры явления.

К таковым, например, относятся: показатель структуры причин смертности, показатель структуры причин младенческой смертности, показатель структуры заболеваемости, показатели распределения населения по полу, образованию, месту жительства, возрастной состав населения, удельный вес детей в структуре населения и т.д.

Методика расчета: э.п. = (часть явления / целое явление) х основание.

Основание – чаще всего 100, экстенсивный показатель выражается в %,

может быть I, экстенсивный показатель выражается в долях.

Интенсивный показатель – показатель частоты явления в среде, которая данное явление продуцирует.

Методика расчета: и.п. = (явление / среда, кот. данное явление продуцирует) х основание

Среда – чаще всего численность населения.

Общий интенсивный показатель – тот, при расчете которого средой выступает численность населения.

Может быть определенная группа населения, часть численности населения. Специальный интенсивный показатель – тот, при расчете которого средой выступает определенная часть (группа) населения. Пример специального интенсивного показателя: показатель общей плодовитости, показатель брачной плодовитости, показатель повозрастной плодовитости. Показатель общей плодовитости = (число рождений у женщин фертильного возраста (15-49 лет) / число женщин фертильного возраста (15-49 лет)) х 100.

Основание:

100 – так рассчитываются, например, показатель летальности, показатель мертворождаемости, которые выражаются в %.

Показатель летальности = (число умерших / число больных) х 100

Показатель мертворождаемости = (число детей, родившихся мертвыми / число детей, родившихся живыми и мертвыми) х 100.

На 100 работающих рассчитываются и выражаются показатели заболеваемости с временной потерей трудоспособности.

Показатель частоты дней временной нетрудоспособности = (число дней временной нетрудоспособности / число работающих) х100

Показатель частоты случаев временной нетрудоспособности = (число случаев временной нетрудоспособности / число работающих) х 100.

1000 – это основание, которое чаще всего используется при расчете санитарно-статистических показателей. Так рассчитываются, например, показатели заболеваемости, болезненности, рождаемости, смертности, младенческой смертности, естественного прироста и др. Они выражаются в %о (промилях).

Рождаемость = (число родившихся за год / среднегодовая численность населения) х 1000

Смертность = (число умерших за год / среднегодовая численность населения) х 1000

Заболеваемость = (совокупность заболеваний, зарегистрированных впервые в жизни в данном году / среднегодовая численность населения) х 1000.

10 000 – так рассчитываются, например, показатели заболеваемости и смертности по отдельным причинам. На 10 000 населения рассчитываются показатели инвалидности. Названные показатели выражаются в %оо (продецимилях).

Показатель первичной инвалидности = (число лиц, которым впервые в жизни установлена группа инвалидности / численность населения) х 10 000

100 000 – на 100 000 детей, родившихся живыми, например, рассчитывается и выражается показатель материнской смертности.

Материнская смертность = (число женщин, умерших во время беременности, родов и в первые 42 дня послеродового периода / число детей, родившихся живыми) х 100 000.

На 100 000 населения могут рассчитываться показатели заболеваемости смертности по отдельным причинам. Названные показатели выражаются в %оо (просантимилях).

Показатель соотношения – это показатель частоты явления в среде, которая данное явление не продуцирует. Он характеризуется отношением двух статистических совокупностей, не связанных между собой, а сопоставимых только логически, по их содержанию.

Методика расчета: п.с. = (явление / среда, кот. данное явление не продуцирует) х основание.

Пример: показатель обеспеченности населения врачами, средним медицинским персоналом, койками. Они рассчитываются и выражаются на 10 000 населения.

Показатель наглядности – показатель, который используется для того, чтобы охарактеризовать изменения явления в динамике.

Методика расчета: первоначально исходный или конечный (либо любой другой) уровень принимают за 1 или 100, а затем путем составления пропорций для каждого уровня находят, во сколько раз или на сколько процентов произошло уменьшение либо увеличение.

К другим относительным величинам могут быть отнесены: показатель координации, коэффициент правдоподобия.

Показатель координации характеризует отношение частей целого между собой. Пример: показатели отношения между численностью мужчин и женщин, показатели отношения между числом врачей и средних медицинских работников.

Показатель координации = (число мужчин / число женщин) х 1 000.

Коэффициенты правдоподобия характеризуют соотношения одноименных относительных показателей структуры, рассчитанных на двух разных совокупностях.

 

Динамические ряды, их виды и методика анализа

Динамический ряд – это ряд числовых значений признака (уровней), характеризующих его изменения во времени.

Виды: 1) простой – состоит из абсолютных величин;

2) сложный – состоит из относительных и средних величин.

Виды простого динамического ряда:

1) моментный – ряд числовых значений признака, характеризующих его изменения на определенные моменты времени,

2) интервальный – ряд числовых значений признака, характеризующих его изменения за определенные интервалы времени (чаще всего год, пять лет).

Для анализа динамического ряда рассчитывают следующие показатели:

1) абсолютный прирост (снижение) – разность данного уровня и предыдущего;

2) темп роста или снижения – процентное отношение последующего уровня к предыдущему;

3) темп прироста – процентное отношение абсолютного прироста к предыдущему уровню.

При значительных колебаниях уровней динамического ряда могут использоваться методики выравнивания динамического ряда: выравнивание по способу наименьших квадратов, приведение рядов к одному основанию, расчет групповой и скользящей средней, укрепление интервала.

 

Методика расчета стандартизованных показателей

И их применение в медицине.

Метод стандартизации. Интенсивные показатели не всегда правильно выявляют закономерности отражаемых ими явлений, т.к. на их величину влияет структура совокупности, из которой они исчислены.

Метод стандартизации применяется в том случае, когда при сравнении интенсивных показателей, вычисленных из неоднородных по своему составу совокупностей (сред), необходимо устранить влияние на них определенного фактора (среды). Например, необходимо сравнить смертность населения в двух районах А и Б. Неправильно было бы сделать вывод, не учитывая структуру населения в указанных районах. Общеизвестно, что на показатели смертности влияют такие факторы, как возрастной и половой состав населения.

 

Существует несколько способов стандартизации:

1) прямой;

2) косвенный;

3) обратный.

Выбор способа стандартизации зависит от имеющихся в нашем распоряжении исходных данных. Наиболее простым и точным является прямой способ стандартизации. Для его применения необходимо иметь распределение сравниваемого явления по устраняемому признаку и такое же распределение среды, в которой оно наблюдается. Например, пусть необходимо сравнить частоту заболеваемости с ВУТ (в случаях) в двух цехах, устранив при этом различия в возрастном составе работающих.

Необходимые исходные данные:

Возрастные группы (в годах)	Цех № 1	Цех № 2
число работающих	число случаев нетрудоспособности	число работающих	число случаев нетрудоспособности
до 19 20-39 40-59 60 и старше
ИТОГО:

 

Прямой способ стандартизации состоит из следующих этапов:

I этап – вычисление интенсивных показателей.

В нашем примере – вычисление частоты случаев нетрудоспособности в целом по цехам и в каждой возрастной группе:

Рассчитываем общий интенсивный показатель для цеха № 1:

1000 работающих – 1345 случав

100 работающих - х

 

В возрасте до 19 лет (для цеха № 1) – частный интенсивный показатель:

120 работающих – 80 случаев

100 работающих - х

и т.д. (для цеха № 1 и цеха № 2).

Полученные результаты заносим в таблицу:

Возраст группы (в годах)	Частота случаев нетрудоспособности на 100 работающих
Цех № 1	Цех № 2
до 19 20-39 40-59 60 и старше	66,7 105,3 170,0 185,0	70,0 115,0 165,0 170,0
ИТОГО:	134,5	110,1

II этап прямого способа стандартизации – выбор стандарта. За стандарт обычно берут распределение по устраняемому фактору одной из сред, либо их сумму, либо подсумму. Однако, стандарт можно выбрать любой, по нашему смотрению. В нашем примере за стандарт можно взять распределение работающих в цехе № 1, либо в цехе № 2, либо средний возрастной состав по цехам № 1 и № 2, либо любое другое распределение работающих по возрасту. Пусть за стандарт мы возьмем сумму работающих в обоих цехах, т.е. в возрасте до 19 лет: 120 + 200 = 320 работающих, в 20-39 лет – 380 + 500 = 880 работающих и т.д.

III этап – наиболее ответственный – вычисление ожидаемых чисел. Необходимо вычислить, какова была бы величина сравниваемого явления, если бы частные интенсивные показатели остались прежними, а распределение среды было бы таким, как по стандарту.

В нашем примере вычисляем, сколько было бы случаев нетрудоспособности в цехе № 1 и № 2. если бы повозрастные показатели работающих в каждой возрастной группе было бы таким, как по стандарту и одинаковым (что очень важно) в цехе № 1 и № 2. Найдем сколько случаев нетрудоспособности было бы у работающих в возрасте до 19 лет в цехе № 1:

на 100 работающих – 66,7 случаев

на 320 работающих - х случаев

В том же цехе № 1 в возрасте 20-39 лет число случаев нетрудоспособности составило бы:

на 100 работающих – 105,3 случая

на 880 работающих - х

и т.д.

 

Всего в цехе № 1 было бы: 213,44 + 926,64 + 816 + 222 = 2178,03 случая. Результаты вычисления заносим в таблицу:

Возраст группы (в годах)	Стандарт (число работающих)	«Ожидаемое» число случаев нетрудоспособности
Цех № 1	Цех № 2
до 19 20-39 40-59 60 и старше		213,44 926,64 816,00 222,00	224,0 1012,0 792,0 204,0
ИТОГО:		2178,08	2232,0

 

IV этап – вычисление стандартизованных показателей и их сравнение.

Стандартизованные показатели рассчитываются, как и обычные интенсивные показатели, на величину стандарта. В нашем примере рассчитываем частоту случаев нетрудоспособности на 100 рабочих. В цехе № 1 на 1800 работающих было бы всего 2178,1 случаев нетрудоспособности, следовательно, на 100 работающих – х.

В цехе № 2:

Выводы: если бы возрастной состав работающих в цехах был одинаковым, то частота случаев заболеваемости в цехе № 2 была бы выше, чем в цехе № 1. Более высокий интенсивный показатель частоты случаев нетрудоспособности в цехе № 1 (134,5) обусловлен тем, что в нем среди работающих лиц старше 40 лет составляют 50%, а в цехе № 2 – только 12,5%.

Стандартизованные показатели могут быть использованы только для сравнения, их величина является условной, зависящей от выбора условий (стандарта), она не дает представления об истинном размере того или иного явления. Поэтому указывать величину стандартизованного показателя не следует. На основании сравнения стандартизованных показателей можно судить, где выше или ниже величина явления при условии ускорения влияния на него неоднородного состава сравниваемых совокупностей или (проще), как соотносились бы интенсивные показатели при устранении влияния на них определенного фактора.

Косвенный способ стандартизации применяется в тех случаях, когда мы располагаем данными о распределении среды по устраняемому фактору, но неизвестно распределение сравниваемого явления.

Обратный (косвенному) способ стандартизации применяется в тех случаях, когда известны лишь данные о распределении (составе) сравниваемого явления, но нет распределения совокупностей (среды).

В некоторых случаях необходимо применение метода стандартизации для элиминирования (устранения) одновременно двух и более факторов. В этом случае проведение стандартизации требует построения комбинационной таблицы, в которой сочетались бы эти факторы.

Вариационный ряд, его виды

Вариационный ряд – это ряд числовых значений признака.

Основные характеристики вариационного ряда: v – варианта, р – частота ее встречаемости.

Виды вариационного ряда:

1) по частоте встречаемости варианты: простой – варианта встречается один раз, взвешенный – варианта встречается два и более раз;

2) по расположению варианты: ранжированный – варианты расположены в порядке убывания и возрастания, неранжированный – варианты записаны без определенного порядка;

3) по объединению вариант в группы: сгруппированный – варианты объединены в группы, несгруппированный – варианты необъединены в группы;

4) по величине варианты: непрерывный – варианты выражены целым и дробным числом, дискретный – варианты выражены целым числом, сложный – варианты представлены относительной или средней величиной.

Вариационный ряд составляется и оформляется с целью расчета средних величин.

Форма записи вариационного ряда:

v	vp	p	d	d^2	d^2p	dp
. . .	. . .	. . .	. . .	. . .	. . .	. . .
∑v	∑vp	n=∑p		∑d^2	∑d^2p	∑dp