
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула Бернулли и Пуассона.Содержание книги Поиск на нашем сайте
Формула Бернулли и Пуассона. Рассмотрим событие А, кот. может наступить с вероят-тью р в каждом из n испытаний. При чем вероят-ть наступления события А не зависит от его наступления в предыдущих испытаниях. Такие испытания принято называть независимыми. Теорема Бернулли. Если вероят-ть наступления события А в каждом испытании постоянна, то вероят-ть того, что событие А наступит m раз в серии из n независимых испытаний равна:
Док-во: n=3 m=2 В -в 3-ех независ. испытаниях событие А наступило 2 раза. А1 -событие А наст. в 1-ом испытании; А2 -во 2-ом испытании; А3 -в 3-ем испытании. По условию Теорема Пуассона. Если вероят-ть p наступления события А в каждом испытании постоянна и стремится к 0 при неограниченном увеличении числа испытаний Док-во: Пусть даны вер-ть наступления события А в одном испытании р и число независ. испытаний n. Обозначим
При достаточно большом n и сравнительно небольшом m, все скобки, за искл. предпослед, можно принять равным единице, т.е.
Локальная и интегральная теоремы Муавра-Лапласа. Локальная теорема. Если вероят-ть р наступления события А вкаждом испытании постоянна и отлично от 0 и 1, то вероят-ть того, что событие А наступит m раз в n независимых испытаниях при достаточно большом числе испытаний
Интегральная теорема. Если вероят-ть р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероят-ть того, что число m наступления события A заключено в пределах [a;b] при достаточно большом числе независимых испытаний
где
Теорема Муавра-Лапласа применима для случая, когда
11. Способы задания закона распред-ния дискретных СВ. Их св-ва. Случайной наз. величина, кот. в рез-те испытания принимает то или иное значение, заранее неизвестно какое именно. Различают дискретные и непрерывные СВ. СВ наз. дискретной, еслиона принимает изолированные друг от друга возможные значения, число кот. может быть как конечным, так и бесконечным. Ряд распред-ния дискретной СВ – это табл., состоящая из 2-ух строк, в одной из кот. указаны возможные значенияуказанной величины, во 2-ой – соответствующие им вероятности. События образуют полную группу, поэтому сумма их вероятностей будет равна 1.
Ф-ия распределения СВ обозначается F(x). Наз. вероят-ть того, чтоСВ Х принимает значение находящееся левее х.
Св-ва: 1) F(x) – неубывающая ф-ия, т.е. 2) F(-
12. Способы задания закона распред-ния непрерывных СВ. Св-ва. Случайной наз. величина, кот. в рез-те испытания принимает то или иное значение, заранее неизвестно какое именно. СВ наз. непрерывной, если её закон распределения можно представить в виде непрерывной ф-ии. Закон распред-ния непрерыв. СВ дается в виде ф-ии распред-ния F(x) и плотности распред-ния f(x). F(x) непрерыв. СВ обладает св-вом непрерывности. f(x) – это производная от ф-ии рапред-ния F(x). Св-ва: 1)
Ф-ию распред-ния непрерыв. СВ можно опред-ть по формуле:
Закон больших чисел. Неравенство Маркова. В узком смысле закон больших чисел – это ряд теорем, в каждой из кот. устанавливается при тех или иных условиях факт приближения средних характеристик большого числа испытаний к некот. пост. величинам. В широком смысле – это некот. общие принципы, согласно кот. совокупное действие большого числа случайных факторов приводит к рез-ту почти независящему от случая, т.е. при большом числе СВ их средний рез-т перестает быть случайным и может быть предсказан с большой степенью определенности. Неравенство Маркова: Если СВ Х принимает только неотриц. значения и имеет мат. ожидание Мх, то для любого числа А > 0 выполняется неравенство:
Док-во: Х=(x1,x2…xn) P(X=x i)=p i; i= Выберем, что
Заменив возможное значение хk+1, xk+2…xn на А>0 в послед. неравенстве, то получаем более строгое неравенство, т.е.
Важнейшей задачей выборочного метода явл. оценка параметров (характер-ик) генеральной совокуп-ти по данным выборки.
Точечная оценка параметров распред-ия. Требования к ф-иям выборки. Точечной оценкой
Т.к. элементы выборки носят случайный характер, следовательно и оценка параметра К наиболее осн. св-вам оценок параметров распред-ия отн-ся: св-ванесмещенности; состоятельности и эффективности. Оценка Оценка Оценка Основные понятия математической статистики. Опр. Мн-во всех допустимых значений признака Х, обеспечивающие возмож-ть получения его закона распред-ия и всех числ. характер-к с исчерпывающей точностью наз. генеральной совокуп-тью. Опр. Ограниченный объем данных ген. совокуп-ти наз. выборкой Опр. Рез-ты рассчетов, полученные по огранич. Объему исходных данных содержит элемент неопред-ти, при этом появл. Различ. Предложения отн-но их истинных значений. Такие предложения наз. стат. гипотизами. Виды выборки: 1)Повторная – каждый отобранный объект перед выбором след. возвращается в ген. совок-ть; 2) Бесповторная – отобранный объект в ген. совок-ть не возвращается. Замечание. Для того, чтобы по исследованию выборки можно было сделать выводы о поведении интересующего нас признака ген. совокуп-ти, нужно, чтобы выборка правильно представляла пропорции ген. совок-ти, т.е. была репрезентативной (представительной). Учитывая закон больших чисел, можно утверждать, что это условие выполняется, если каждый объект выбран случайно, причем для любого объекта вер-ть попасть в выборку одинакова.
Гистограмма распред-ия. Гистрограмма распред-ия – это ступенчатая фигура состоящая из прямоугольников, ширина кот. равна шагу гистограммы распред-ия, а высота числу элементов или доли элементов выборки, оказавшихся в соответств. интервале гистограммы. Шаг распростр. гистограммы: где
Формула Бернулли и Пуассона. Рассмотрим событие А, кот. может наступить с вероят-тью р в каждом из n испытаний. При чем вероят-ть наступления события А не зависит от его наступления в предыдущих испытаниях. Такие испытания принято называть независимыми. Теорема Бернулли. Если вероят-ть наступления события А в каждом испытании постоянна, то вероят-ть того, что событие А наступит m раз в серии из n независимых испытаний равна:
Док-во: n=3 m=2 В -в 3-ех независ. испытаниях событие А наступило 2 раза. А1 -событие А наст. в 1-ом испытании; А2 -во 2-ом испытании; А3 -в 3-ем испытании. По условию Теорема Пуассона. Если вероят-ть p наступления события А в каждом испытании постоянна и стремится к 0 при неограниченном увеличении числа испытаний Док-во: Пусть даны вер-ть наступления события А в одном испытании р и число независ. испытаний n. Обозначим
При достаточно большом n и сравнительно небольшом m, все скобки, за искл. предпослед, можно принять равным единице, т.е.
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 403; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.94.180 (0.009 с.) |

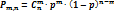 , (1-p) = q;
, (1-p) = q;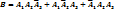

 . При чем
. При чем  , то вероят-ть того, что событие А наступит m раз в n независимых испытаниях равна:
, то вероят-ть того, что событие А наступит m раз в n независимых испытаниях равна:  ;
; . Откуда
. Откуда  . Подставим в формулу Бернулли:
. Подставим в формулу Бернулли:
 Учитывая то, что n достаточно велико, правую часть можно рассмотреть при
Учитывая то, что n достаточно велико, правую часть можно рассмотреть при  , т.е. найти предел.
, т.е. найти предел.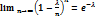 .Получим
.Получим 

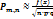 , где
, где 
 ;
; ,
, ;
; ;
;  ;
;


 х2 > x1
х2 > x1  F(x2) > F(x1);
F(x2) > F(x1); )=0; 3) F(
)=0; 3) F(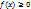 ,
,  R (для любых х принадлежащих R); 2) f(-
R (для любых х принадлежащих R); 2) f(- 


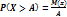 ;
; . A>0
. A>0
 i=
i= 
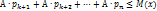



 (тэта)– параметр распред-ия
(тэта)– параметр распред-ия  наз. всякую ф-ию рез-тов наблюдений над признаком х, с помощью кот. судят о значении параметра
наз. всякую ф-ию рез-тов наблюдений над признаком х, с помощью кот. судят о значении параметра 
 . Кач-во используемой ф-ии выборки можно оценить не по отдельным её значениям, а лишь по распред-ию её значений в большой серии испытаний, т.е. по выборочному распред-ию оценки параметра распред-ия.
. Кач-во используемой ф-ии выборки можно оценить не по отдельным её значениям, а лишь по распред-ию её значений в большой серии испытаний, т.е. по выборочному распред-ию оценки параметра распред-ия.
 наз. состоятельной, если она сходится по вер-ти к значению параметра
наз. состоятельной, если она сходится по вер-ти к значению параметра  , т.е. выполняется условие
, т.е. выполняется условие  для любого
для любого  . Выполнение этого условия означает, что с увелич. Объема выборки возрастает наша уверенность в малом по абсолют. величине отклонении оценки
. Выполнение этого условия означает, что с увелич. Объема выборки возрастает наша уверенность в малом по абсолют. величине отклонении оценки  .
. ,
, – макс. элемент выборки;
– макс. элемент выборки;  – мин. эл. выборки;
– мин. эл. выборки;



