
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классич. опред-ие вер-ти события. Формулы комбинаторики.
Исходы эксперимента наз-ся равновозможными, если вер-ти их наступления равны м/у собой. Опр. Вер-ти событий, эксперименты кот. можно разложить на равновозможные исходы, равны отношению числа благоприятствующих исходов к общему числу возможных исходов.
Исход наз-ся благоприятствующим событию А, если его появление влечет появление события А. Формулы комбинаторики: 1) Сочетаниями из n элементов по m наз. соединения, состоящие из m элементов и отличающихся друг от друга составом элементов. Число сочетаний равно числу способов выбора соединений из m элементов из общего числа n элементов. 2) Размещениями из n элементов по m наз. соединения, состоящие из m элементов и отличающиеся друг от друга либо составом, либо порядком их следования. 3) Перестановками из n элементов наз. соединения, состоящие из n элементов и отличающиеся друг от друга порядком следования элементов. 4) Если в сочетании из n эл-тов по m некот. эл-ты повторяются, то их наз. сочетанием с повторением: 5) Если в размещениях из n эл-тов по m некот. эл-ты повторяются, то их наз. размещение с повторением:
Геометрическое определение вероятности события. Согласно геометрич. схеме опред-ия вер-ти. Вер-ть события, эксперимент по воспроизведению кот. можно разложить на бесконечное число равно возможных исходов, равна отшению меры благоприятствующей данному событию области к мере всей области. m(S) – мера всей обл. В кач-ве меры может выступать длина отрезка, площадь фигуры или объем тела. В обл. S появл. случайная точка. Внутри обл. S выделяются замкнутые обл. G1, G2 и G3, тогда вер-ть того, что случайная точка обл. S окажется в замкнутых обл. равна:
21.Точные законы распред-ия С.В. Распред-ие Стьюдента. К точным относятся законы распред-ия непрерывных С.В, в формуле плотности распред-ия вер-тей кот. присутствуют только точные значения параметров, но никак ни значения определяемых по статистич. данным. Пусть мы имеем С.В. V, распределенную по закону Получившийся в результате исследования закон распределения величины T получил название распред-ие Стьюдента. Ф-ия плотности этого распред-ия имеет вид:
Параметр n обозначает число степеней свободы.
22.Точные законы распред-ия С.В. Распред-ие Фишера-Снедекора. К точным относятся законы распред-ия непрерывных С.В, в формуле плотности распред-ия вер-тей кот. присутствуют только точные значения параметров, но никак ни значения определяемых по статистич. данным. Пусть две независим. С.В. U и V распределены по закону
Всегда f(x) > 0 23. Понятие двумерной дискретной СВ и таблица её распред-ия. Опр. ДвумернаяС.В. (X; Y) наз. дискретной, если С.В. X и Y дискретны, т.е.конечны. Если С.В. Х может принимать только значения x1,x2…xn, а С.В. Y – значения y1, y2…yn, то двумерный случайныя вектор (X; Y) может принимать только пары значений Функция распред-ия двумерной С.В. Опр. ДвумернаяС.В. (X; Y) наз. дискретной, если С.В. X и Y дискретны, т.е.конечны. Опр. Функцией распред-ия F(x, y) двумерной С.В. (X,Y) наз. вер-ть того, что X < x, а Y < y. F(x,y) = p(X < x, Y < y) Замечание. Определение ф-ии распред-ия справедливо как для непрерывной, так и для дискретной С.В. Св-ва: 1) 0 <F(x, y)< 1, т.к. F(x, y)явл. вер-тью; 2) F(x, y)есть неубывающая ф-ия по каждому аргументу. F(x2, y) 3) Имеет место предельное соотношение:
4) При y = При x =
|
|||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 225; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.112.220 (0.022 с.) |
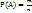 , где m - это число благоприятных событий А, n - общее число возможных исходов.
, где m - это число благоприятных событий А, n - общее число возможных исходов.

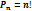
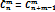

 , где m(G) – мера благоприятствующей обл.
, где m(G) – мера благоприятствующей обл.
 с n степенями свободы. Также задана С.В. Z, распределенная по закону Гаусса. С.В. V и Z независимы. Сконструируем из них новую С.В. T по формуле:
с n степенями свободы. Также задана С.В. Z, распределенная по закону Гаусса. С.В. V и Z независимы. Сконструируем из них новую С.В. T по формуле: 
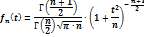
 .
. Исследования закона распред-ия С.В. F показало, что ф-ия плотности этого распред-ия имеет вид:
Исследования закона распред-ия С.В. F показало, что ф-ия плотности этого распред-ия имеет вид:
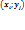 , где,
, где, 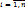 j
j  . Также, как и в одномерном случае, распред-ие двумерной дискретной С.В. естественно описывается с помощью таблицы:
. Также, как и в одномерном случае, распред-ие двумерной дискретной С.В. естественно описывается с помощью таблицы: 
 F(x1, y), еслиx2 > x1; F(x, y2)
F(x1, y), еслиx2 > x1; F(x, y2) 
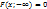


 ф-ия распред-ия двумерной С.В. становится ф-ий распред-ия составляющей X:
ф-ия распред-ия двумерной С.В. становится ф-ий распред-ия составляющей X: 




