
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка гипотезы о равенстве дисперсий двух совокупностей.Содержание книги
Поиск на нашем сайте
Сравнение двух выборочных дисперсий из нормальных совокуп-тей. Для опред-ия того, относятся ли две выборки к одной и той же ген. совок-ти. Проверяется гипотеза вида Статистика для проверки гипотезы имеет вид В случае принадлежности выборок норм. закону и справедливости H0 эта статистика подчинятся F – распред-ию Фишера с числом степеней свободы В зависимости от альтернативы критерий может быть односторонним
Проверка гипотезы о равенстве средних двух совокупностей при известных дисперсиях. Значение дисперсий ген. совокуп-ти признака X и Y известны. Это В кач-ве стат-ки критерия рассматривается
При заданном уровне значимости а) если б) если в) если В противном случае во всех 3-х случаях осн. гипотеза отвергается в пользу конкурирующей.
Проверка гипотезы о равенстве средних двух совокупностей при неизвестных дисперсиях. Значение дисперсий ген. совокуп-тей X и Y неизвестны, но они равны м/у собой. Тогда рассматр-ся числ. критерий
распределенная по закону Стьюдента со степенями свободы а) б) в) В противном случае H0 отвергается в пользу H1.
Проверка гипотезы о равенстве дисперсий двух совокупностей. Сравнение дисперсий двух норм. распределенных ген. совок-тей H0: H1: а) Для проверки указанной гипотезы рассмотр. С.В.
С.В. F распред-на по закону Фишера со степенями свободы При заданной надежности а) б) и в) Если
Гистограмма распред-ия. Гистрограмма распред-ия – это ступенчатая фигура состоящая из прямоугольников, ширина кот. равна шагу гистограммы распред-ия, а высота числу элементов или доли элементов выборки, оказавшихся в соответств. интервале гистограммы.
Шаг распростр. гистограммы: где
Проверка гипотезы о соответствии эмпирич. закона распред-ия теоретич. Проверяется гипотеза о соответствии эмпирич. закона распред-ия теоретическому.
степенями свободы k – число разрядов гистограммы; r – число параметров теоретич. закона распред-ия;
n – объем выборки; При заданной надежности
Если
Понятие интерв-ной оценки параметров распред-ия. Доверит. интервал для неизвест. мат. ожидания. Опр. Доверит. интервал по данным одной выборки и ориентированный на покрывании им истинного значения параметра с заданной надежностью Опр. Оценка параметра распред-ия на основе доверит. интервала наз. интервальной оценкой параметра. Распред-ие Стьюдента: При построении доверительного интервала, сделаем след. подстановки:
Для того чтобы построить интервал, в кот с заданной вер-тью P лежит истинное значение
Понятие интерв-ной оценки параметров распред-ия. Доверит. интервал для дисперсии. Опр. Доверит. интервал по данным одной выборки и ориентированный на покрывании им истинного значения параметра с заданной надежностью Опр. Оценка параметра распред-ия на основе доверит. интервала наз. интервальной оценкой параметра. 323 стр.
|
|||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 402; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.49.198 (0.006 с.) |

 .
.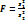
 т.е.
т.е. 
 или двусторонним
или двусторонним  В многочисленных источниках подчеркивается, что результат проверки может сильно зависеть даже от небольших отклонений от нормального распред-ия.
В многочисленных источниках подчеркивается, что результат проверки может сильно зависеть даже от небольших отклонений от нормального распред-ия. .
.
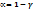 опред-ся критич. Значение распред-ся Гаусса(
опред-ся критич. Значение распред-ся Гаусса( ).
). , то осн. гипотеза не отвергается.
, то осн. гипотеза не отвергается. , то осн. гипотеза не отвергается.
, то осн. гипотеза не отвергается.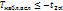 , то осн. гипотеза не отвергается.
, то осн. гипотеза не отвергается.
 . При заданной надежности
. При заданной надежности  в степенях свободы k опред-ся границы критич. точки (
в степенях свободы k опред-ся границы критич. точки ( ).
). Если
Если  , то H0 – не отвергается
, то H0 – не отвергается Если
Если  , то H0 – не отвергается
, то H0 – не отвергается Если
Если  , то H0 – не отвергается
, то H0 – не отвергается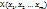 и Y
и Y  .
.
 ; б)
; б)  ; в)
; в)  ;
;
 и
и  .
.

 , то нет оснований отвергать осн. гипотезу. В противном случае осн. гипотеза отвергается в пользу конкурирующей на уровне значимости
, то нет оснований отвергать осн. гипотезу. В противном случае осн. гипотеза отвергается в пользу конкурирующей на уровне значимости  .
. ,
, – макс. элемент выборки;
– макс. элемент выборки;  – мин. эл. выборки;
– мин. эл. выборки;
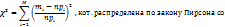
 , где
, где 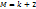 ,
, – число эл. выборки, оказавшихся в i- том разряде гистограммы;
– число эл. выборки, оказавшихся в i- том разряде гистограммы; – теоретич. вер-ть попадания признака X в i- тый разряд гистограммы;
– теоретич. вер-ть попадания признака X в i- тый разряд гистограммы; опред-ся границы критич. обл. по табл. распред-ия Пирсона.
опред-ся границы критич. обл. по табл. распред-ия Пирсона.
 , то можно утверждать, что признак Х на уровне значимости
, то можно утверждать, что признак Х на уровне значимости  , где z – С.В., распределенная нормально с мат. ожиданием = 0 и дисперсией = 1, V – C.В, распределенная по закону
, где z – С.В., распределенная нормально с мат. ожиданием = 0 и дисперсией = 1, V – C.В, распределенная по закону  с v степенями свободы.
с v степенями свободы. . В кач-ве V выберем:
. В кач-ве V выберем: тогда учитывая, что
тогда учитывая, что  получим
получим
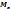 .
.



