
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Осн. Правила и формулы комбинаторикиСодержание книги
Поиск на нашем сайте
ПРЕДМЕТ ТЕОРИИ ВЕРОЯТНОСТИ Теория вероятностей – математическая дисциплина, изучающая закономерности в случайных явлениях. Случайным в теории вероятностей называют событие, которое при данном испытании, в данном опыте может либо произойти, либо не произойти и для которого имеется определенная вероятность его наступления. опр: экспериментом или опытом наз осущ-е намеч-го дейст-я и получение его рез-та. предметом ТВ, кот изучает закономерности случ явлений явл модели экспер-в со случ исходами. элем соб-ем наз каждый из равнов-х рез-в испытаний. всякий мыслимый рез экспет-та наз элем соб-ем и оброзн ω1, ω2,…, ωn. простр-вом элем соб-й наз мн-во всех взаимно исключающих экспер-та. обозн. Математическая модель случайного эксперимента включает в себя: 1) построение множества элементарных исходов 2) описание множества событий для данного эксперимента; 3) задание вероятностного распределения на множестве событий.
2. СЛУЧАЙНЫЕ СОБЫТИЯ И ИХ КЛАССИФИКАЦИЯ Из элементарных исходов можно составить более сложное событие. Результат испытания называется событием, независимо от его значимости. Результат испытания, который нельзя заранее прогнозировать, называется случайным событием. опр:Каждое случайное событие опр:Два события называются совместными (совместимыми) в данном опыте, если появление одного из них не исключает появления другого. Два события называются несовместными (несовместимыми) в данном опыте, если они не могут произойти вместе при одном и том же испытании. Несколько событий называются несовместными, если они попарно несовместны. Другими словами, события опр: Достоверным называют событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий Событие, совпадающее с пустым множеством опр: События называют равновозможными, если нет основания полагать, что одно событие является более возможным, чем другие.
3.ДЕЙСТВИЯ НАД СОБЫТИЯМИ
3.
4. Противоположным (дополнительным) для события
Два события называются противоположными, если появление одного из них равносильно непоявлению другого.
Теоремы сложения вероятностей Теорема: Вероятность суммы конечного числа несовместных событий
Теорема: Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
8. Теоремы умножения вероятностей Теорема: Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие имело место:
Теорема: Вероятность произведения конечного числа событий равна произведению их условных вероятностей относительно произведения предшествующих событий: Р(А1·А2·…·Аn)= Р(А1)·(А2)·…·Р(Аn) Свойства дисперсии 1. Дисперсия постоянной величины равна нулю. 2. 3. 4. 5. D(X-Y)= D(X)-D(Y) ОПР: Средним квадратичным отклонением
17. НЕПРЕРЫВНО РАСПРЕДЕЛЕННАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА. Математическим ожиданием непрерывной случайной величины
Дисперсией непрерывной случайной величины
Среднее квадратичное отклонение непрерывной случайной величины
18. БИННОМИНАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ ОПР: законом распределения случайной величины наз соот-ие между значениями случ-й величины и их верот-ми. Теорема. Математическое ожидание числа появлений события Теорема. Дисперсия числа появлений события Биномиальный закон распределения часть приходится применять в условиях, когда число независимых испытаний велико. Вычисление вероятностей по формуле Бернулли при этом усложняется, поэтому представляет интерес асимптотическое приближение для биномиального закона, справедливое при больших 1. Когда при увеличении числа испытаний математическое ожидание рассматриваемой случайной величины 2. Когда при увеличении числа испытаний остается постоянным произведение
19. РАСПРЕДЕЛЕНИЕ ПУАСОНА СЛУЧАЙНОЙ ВЕЛИЧИНЫ ОПР:Случайная величина
ТЕОРЕМА: М случ величины распред-ой по закону Пуассона =λ Д=λ, ϭ(х)=
Нормальное распределение ОПР: Нормальным называется такое распределение случайной величины
где
ТЕОРЕМА: М(х)=m D(x)=ϭ ϭ(x)=ϭ
21. ОПР: Математическое ожидание дискретной случайной величины – это сумма парных произведений всех возможных ее значений на соответствующие вероятности:
где Свойства дисперсии 1. Дисперсия постоянной величины равна нулю. 2. 3. 4. 5. D(X-Y)= D(X)-D(Y)
ПРЕДМЕТ ТЕОРИИ ВЕРОЯТНОСТИ Теория вероятностей – математическая дисциплина, изучающая закономерности в случайных явлениях. Случайным в теории вероятностей называют событие, которое при данном испытании, в данном опыте может либо произойти, либо не произойти и для которого имеется определенная вероятность его наступления. опр: экспериментом или опытом наз осущ-е намеч-го дейст-я и получение его рез-та. предметом ТВ, кот изучает закономерности случ явлений явл модели экспер-в со случ исходами. элем соб-ем наз каждый из равнов-х рез-в испытаний. всякий мыслимый рез экспет-та наз элем соб-ем и оброзн ω1, ω2,…, ωn. простр-вом элем соб-й наз мн-во всех взаимно исключающих экспер-та. обозн. Математическая модель случайного эксперимента включает в себя: 1) построение множества элементарных исходов 2) описание множества событий для данного эксперимента; 3) задание вероятностного распределения на множестве событий.
2. СЛУЧАЙНЫЕ СОБЫТИЯ И ИХ КЛАССИФИКАЦИЯ Из элементарных исходов можно составить более сложное событие. Результат испытания называется событием, независимо от его значимости. Результат испытания, который нельзя заранее прогнозировать, называется случайным событием. опр:Каждое случайное событие опр:Два события называются совместными (совместимыми) в данном опыте, если появление одного из них не исключает появления другого. Два события называются несовместными (несовместимыми) в данном опыте, если они не могут произойти вместе при одном и том же испытании. Несколько событий называются несовместными, если они попарно несовместны. Другими словами, события опр: Достоверным называют событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий Событие, совпадающее с пустым множеством опр: События называют равновозможными, если нет основания полагать, что одно событие является более возможным, чем другие.
3.ДЕЙСТВИЯ НАД СОБЫТИЯМИ
3.
4. Противоположным (дополнительным) для события
Два события называются противоположными, если появление одного из них равносильно непоявлению другого.
ОСН. ПРАВИЛА И ФОРМУЛЫ КОМБИНАТОРИКИ Выбор с возвр-нием: кажд выбр-ный шарик возвр-ся в урну, т.е. кажд из · Выбор без возвр-ния: выбр-ные шарики в урну не возвр-ся, и в получ наборе не могут встреч-ся одни и те же номера (выборка без повторений). · Выбор с учетом порядка: два набора номеров шариков считаются различными, если они отличаются составом или порядком номеров. · Выбор без учета порядка: два набора номеров шариков считаются различными, если они отличаются составом. Наборы, отличающиеся лишь порядком следования номеров, считаются одинаковыми. Размещ-ми Теорема. Общее кол-во выборок в схеме выбора Соединения из Общее кол-во выборок в схеме выбора Соч-ми Теорема. Общее кол-во выборок в схеме выбора
Теорема. Общее количество выборок в схеме выбора Теорема. Общее количество выборок в схеме выбора
5. КЛАССИЧЕСКОЙ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ Вероятность
0≤m≤n 0≤m/n≤1 0≤P(A)≤1 Т.о. вер-ть любого соб-я есть неотриц. число превышающее 1. если Р(А)=0, то соб-е А невозможное. если Р(А)=1, то соб-е А достоверное. Равновозм-ое элем-ое соб-е явл равновероятностным, т.е. обладает одной и той же вер-ю. Т1. А=В, Р(А)=Р(В) Т2. если АϵВ, Р(А)≤Р(В) Т3. Ā есть противоп соб-е к соб-ю А, то Р(А)+Р(Ā)=1
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 246; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.205.114 (0.007 с.) |


 ;
; определяется как подмножество в множестве элементарных событий
определяется как подмножество в множестве элементарных событий  наступает (т.е. принадлежит подмножеству
наступает (т.е. принадлежит подмножеству  совместны, если соответствующие множества
совместны, если соответствующие множества  . Невозможным называют событие, которое заведомо не произойдет, если будет осуществлена определенная совокупность условий
. Невозможным называют событие, которое заведомо не произойдет, если будет осуществлена определенная совокупность условий  .
. , называется невозможным событием, а событие, совпадающее со всем множеством
, называется невозможным событием, а событие, совпадающее со всем множеством  (
( ) – сумма событий. Это событие, состоящее в том, что произошло хотя бы одно из двух событий
) – сумма событий. Это событие, состоящее в том, что произошло хотя бы одно из двух событий 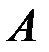 или
или  (не исключающее логическое «или»).
(не исключающее логическое «или»).
 (
( ) – произведение событий. Это событие, состоящее в совместном осуществлении событий
) – произведение событий. Это событие, состоящее в совместном осуществлении событий 
 (множество элементов, принадлежащих
(множество элементов, принадлежащих 
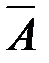 ) называется событие, состоящее из всех исходов, которые не входят в
) называется событие, состоящее из всех исходов, которые не входят в 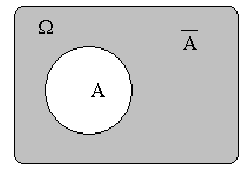

 равна сумме вероятностей этих событий:
равна сумме вероятностей этих событий: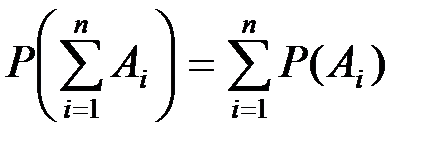 .
. .
. .
.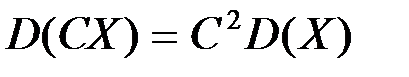


 (или стандартом) случайной величины
(или стандартом) случайной величины  называется корень квадратный из дисперсии
называется корень квадратный из дисперсии 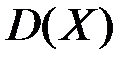 этой величины:
этой величины:  .
.
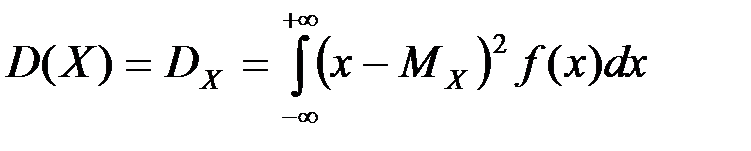 .
. .
. в
в 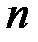 независимых испытаниях равно произведению числа испытаний на вероятность появления события
независимых испытаниях равно произведению числа испытаний на вероятность появления события  .
. тоже неограниченно возрастает (случай постоянного
тоже неограниченно возрастает (случай постоянного  ); при этом биномиальное распределение сходится к нормальному закону, который будет рассмотрен позже.
); при этом биномиальное распределение сходится к нормальному закону, который будет рассмотрен позже. , то есть математическое ожидание рассматриваемой случайной величины остается конечным. Это означает, что вероятность события
, то есть математическое ожидание рассматриваемой случайной величины остается конечным. Это означает, что вероятность события 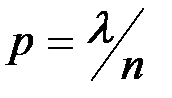 стремится к нулю. В этом случае биномиальное распределение сходится к распределению Пуассона.
стремится к нулю. В этом случае биномиальное распределение сходится к распределению Пуассона. , если эта случайная величина может принимать значения
, если эта случайная величина может принимать значения  , соответствующая вероятность которых определяется по формуле Пуассона, когда
, соответствующая вероятность которых определяется по формуле Пуассона, когда  :
:


 – среднее квадратичное отклонение;
– среднее квадратичное отклонение;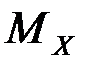 – математическое ожидание случайной величины.
– математическое ожидание случайной величины. ,
, .
.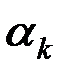 шариков выбир-ся из полной урны. В получ-м наборе, сост-м из
шариков выбир-ся из полной урны. В получ-м наборе, сост-м из  из
из  элем-в по
элем-в по  (
(  ) наз их соед-ния, каждое из кот содержит ровно
) наз их соед-ния, каждое из кот содержит ровно  из
из  элементов по
элементов по 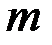 и определяется формулой
и определяется формулой  .
. .
.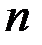 элем-в из
элем-в из  и опр-ся по формуле
и опр-ся по формуле 
 из
из  (
( ) наз такие их соед-я, каждое из кот содержит ровно
) наз такие их соед-я, каждое из кот содержит ровно  .
. с возвращением и с учетом порядка определяется формулой
с возвращением и с учетом порядка определяется формулой 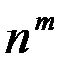 .
. элементов из
элементов из  с возвращением и без учета порядка определяется формулой
с возвращением и без учета порядка определяется формулой
 события
события 



