
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Доверительные интервалы математического ожидания и для дисперсии нормально распределенной случайной величины.Содержание книги
Поиск на нашем сайте
Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение s этого распределения известно. Требуется оценить неизвестное математическое ожидание a по выборочному среднему Будем рассматривать выборочное среднее Выражение для искомого доверительного интервала вычисляется по формуле
37. СТАТИС-АЯ ГИПОТЕЗА, СТАТИС-Й КРИТЕРИЙ, ОШИБКИ ПЕРВОГО И ВТОРОГО РОДА. Статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений. Примеры статистических гипотез: генеральная совокупность распределена по закону Пуассона; дисперсии двух нормальных распределений равны между собой. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза. Следует отметить, что последствия ошибок могут оказаться различными. Если отвергнуто правильное решение «продолжать строительство жилого дома», то эта ошибка первого рода повлечет материальный ущерб; если же принято неправильное решение «продолжать строительство» несмотря на опасность обвала дома, то эта ошибка второго рода может привести к многочисленным жертвам. Иногда, наоборот, ошибка первого рода влечет более тяжелые последствия. Статистическим критерием (или просто критерием) называют случайную величину (обозначим ее через K), которая служит для проверки нулевой гипотезы. Например, если проверяют гипотезу о равенстве дисперсий двух нормальных генеральных совокупностей, то в качестве критерия K принимают отношение исправленных выборочных дисперсий
38. КРИТИЧЕСКАЯ ОБЛАСТЬ, МОЩНОСТЬ КРИТЕРИЯ. Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают. Областью принятия гипотезы (областью допустимых значений) называют совокупность значений критерия, при которых гипотезу принимают. Основной принцип проверки статистических гипотез можно сформулировать так: если наблюдаемое значение критерия принадлежит критической области – гипотезу отвергают, если области принятия гипотезы – гипотезу принимают. Так как критерий K – одномерная случайная величина, то все ее возможные значения принадлежат некоторому интервалу и, соответственно, должны существовать точки, разделяющие критическую область и область принятия гипотезы. Такие точки называются критическими точками. Различают одностороннюю (правостороннюю и левостороннюю) и двустороннюю критические области. Правосторонней называют критическую область, определяемую неравенством Левосторонней называют критическую область, определяемую неравенством Двусторонней называют критическую область, определяемую неравенствами
39. СХЕМА ПРОВЕРКИ СТАТ-ОЙ ГИПОТЕЗЫ. 1. Сформулировать нулевую H0 и альтернативную Н1, гипотезы. 2. Выбрать уровень значимости α. 3. В соответствии с видом выдвигаемой нулевой гипотезы Н0 иыбрать статистический критерий для ее проверки, т. е. — специально подобранную случайную величину К, точное или приближенное распределение которой заранее известно. 4. По таблицам распределения случайной величины К, выбранной в качестве статистического критерия, найти критическое значение Ккр (критйческую точку или точки). 5. На основании выборочных данных по специальному алгоритму вычислить наблюдаемое значение критерия Кнабл 6. По виду конкурирующей гипотезы Н1 определить тип критической области. 7. Определить, в какую область (допустимых значений или критическую) попадает наблюдаемое значение критерия Кна6п, и в зависимости от этого -— принять решение относительно нулевой гипотезы Н0. Можно принять решение относительно нулевой гипотезы Н0 путем сравнения наблюдаемого и критического значения критерия.
41. ПРОВЕРКА ГИПОТЕЗ О РАВЕНСТВЕ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ. КРИТЕРИЙ СОГЛАСИЯ ПИРСОНА. Пусть генеральные совокупности X и У распределены нормально, причем их дисперсии D(X) = ϭ 2х и D(Y) = ϭ2y известны. По независимым выборкам объемов пх и п у, извлеченным из этих совокупностей, найдены выборочные средние X и У. Требуется по выборочным средним, при заданном уровне значимости α проверить гипотезу о равенстве математических ожиданий двух нормально распределенных генеральных совокупностей X и У: Н0: М(Х) = М(У); Н1: М(Х)≠ М(У) До сих пор мы предполагали, что закон распределения генеральной совокупности известен. Если закон распределения неизвестен, но есть основания предполагать, что он имеет определенный вид (назовем его А), то проверяют нулевую гипотезу: генеральная совокупность распределена по закону А. Проверка этой гипотезы производится при помощи специально подобранной случайной величины – критерия согласия. Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения. Имеется несколько критериев согласия, наиболее часто используемым является критерий согласия К.Пирсона («хи квадрат»). Ограничимся применением критерия Пирсона к проверке гипотезы о нормальном распределении генеральной совокупности.
43. ОСНОВНЫЕ ПОНЯТИЯ КОРРЕЛЯЦИОННОГО И РЕГРЕССИОННОГО АНАЛИЗА. Строгая функциональная зависимость реализуется редко, так как случайные величины подвержены действию случайных факторов, причем среди них могут быть и общие для двух или нескольких величин. В этом случае возникает статистическая зависимость. Статистической называют зависимость, при которой изменение одной из величин влечет изменение распределения другой. В частности, статистическая зависимость проявляется в том, что при изменении одной из величин изменяется среднее значение другой – в этом случае статистическая зависимость называется корреляционной. Под регрессией понимается функциональная зависимость между объясняющими переменными и условным математическим ожиданием (средним значением) зависимой переменной Y, которая строится с целью предсказания (прогнозирования) среднего значения Y при фиксированных значениях независимых переменных. Корреляционно-регрессионный анализ включает в ceбя измерение тесноты и направления связи, а также установление аналитического выражения (формы) связи. Задачи корреляционного анализа сводятся к измерению тесноты связи между варьирующими признаками, определению неизвестных причинных связей и оценке факторов, оказывающих наибольшее влияние на результативный признак. Задачи регрессионного анализа лежат в сфере установления формы зависимости, определения функции регрессии, использования уравнения для оценки неизвестных значении зависимой переменной.
48. ЛИНЕЙНАЯ КОРРЕЛЯЦ ЗАВИСИМОСТЬ И ПРЯМЫЕ РЕГРЕСИИ.
49. КОЭФФИЦИЕНТ ЛИНЕЙНОЙ КОРРЕЛЯЦИИ И ЕГО СВОЙСТВА
50. ПОСТРОЕНИЕ ЭМПИРИЧЕСКОГО УРАВНЕНИЯ ПРЯМОЙ РЕГРЕССИИ.
45. ПРОВЕРКА ГИПОТЕЗ О МАТЕМАТИЧЕСКОМ ОЖИДАНИИ СЛУЧАЙНОЙ ВЕЛИЧИНЫ, РАСПРЕДЕЛЕННОЙ ПО НОРМАЛЬНОМУ ЗАКОНУ.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 254; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

 . Найдем доверительные интервалы, покрывающие параметр a с надежностью
. Найдем доверительные интервалы, покрывающие параметр a с надежностью  .
. (т.к.
(т.к.  , как одинаково распределенные независимые случайные величины
, как одинаково распределенные независимые случайные величины  (эти числа также меняются от выборки к выборке). Другими словами, математическое ожидание каждой из этих величин равно a и среднее квадратическое отклонение – s. Так как случайная величина X распределена нормально, то и выборочное среднее
(эти числа также меняются от выборки к выборке). Другими словами, математическое ожидание каждой из этих величин равно a и среднее квадратическое отклонение – s. Так как случайная величина X распределена нормально, то и выборочное среднее  с надежностью
с надежностью  .
. , где
, где  – положительное число.
– положительное число.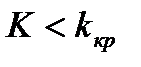 , где
, где  , где
, где  .
.


