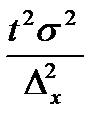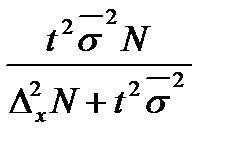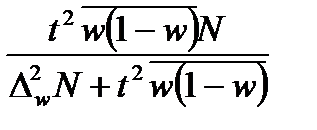Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Статистическое изучение вариацииСодержание книги
Поиск на нашем сайте
Вариацией признака называется его изменение (колеблемость) при переходе от одной единицы наблюдения к другой. Для измерения вариации применяются абсолютные и относительные показатели. К числу важнейших абсолютных показателей относят: - размах вариации: R=Xmax-Xmin - среднее линейное отклонение
- дисперсию
- среднее квадратическое отклонение
Относительные показатели вариации представлены следующими коэффициентами: - коэффициент осцилляции
- относительное линейное отклонение
- коэффициент вариации
В том случае, когда совокупность характеризуется качественным признаком, в частности альтернативным, оценка вариации производится с помощью дисперсии, определяемой по формуле
где p – доля единиц, обладающих интересующим исследователя признаком; g – доля единиц, не обладающих данным признаком. При изучении взаимосвязей социально-экономических явлений исчисляют следующие виды дисперсии: - внутригрупповую (частную), которую исчисляют по каждой группе
и по совокупности в целом как среднюю из внутригрупповых
где Ai – число единиц наблюдения в группе. - межгрупповую, которая характеризует колеблемость частных средних вокруг общей средней:
- общую, которая характеризует вариацию признака по изучаемой совокупности:
Последняя формула в статистике получила название правило сложения дисперсии. В статистических исследованиях широкое распространение получили показатели взаимосвязей явлений, основанные на использовании дисперсии. Например, коэффициент детерминации
характеризующий долю вариации признака-результата под воздействием признака-фактора, положенного в основу группировки, или эмпирическое корреляционное отношение
характеризующее тесноту этой связи.
Контрольные вопросы: 1. Понятие вариации. 2. Необходимость статистического изучения вариации. 3. Абсолютные характеристики измерения вариации, порядок их расчета и сфера их применения. 3.1 Размах вариации. 3.2 Среднее линейное отклонение. 3.3 Дисперсия. 3.4 Среднее квадратическое отклонение. 4. Относительные показатели вариации, методы их исчисления и сфера применения. 4.1 Коэффициент осцилляции. 4.2 Коэффициент среднего линейного отклонения. 4.3 Коэффициент вариации. 5. Основные математические свойства дисперсии. 6. Дисперсия альтернативного признака. 7. Виды дисперсии: общая, внутригрупповая, межгрупповая. 8. Правило сложения дисперсий и его значение в изучении связей социально-экономических явлений. 9. Использование дисперсий при определении коэффициента детерминации и эмпирического корреляционного отношения.
Задание №1 Определить степень колеблемости показателя прибыли, исчислив все показатели вариации. Таблица 22 – Исходные данные
Задание №2 Определить степень колеблемости выработки в бригаде, рассчитав дисперсию с использованием и без использования ее свойств. Таблица 23 – Исходные данные
Задание №3 Определите среднюю выработку 1 рабочего и дисперсию (с использованием и без использования свойств). Таблица 24 – Исходные данные
Задание №4 Определить среднюю прибыль по группе предприятий и дисперсию (с использованием и без использования свойств). Таблица 25 – Исходные данные
Задание №5 По приведенной информации определить среднюю прибыль предприятия и показатели ее вариации. Таблица 26 – Исходные данные
Тема: Выборочное наблюдение Выборочное наблюдение – это такое несплошное наблюдение, при котором обследованию подвергается часть единиц совокупности, а результаты распространяются на всю совокупность. Для того, чтобы выборка полно и правильно представляла генеральную совокупность, необходимо объективно произвести отбор данных. Виды, способы и методы отбора единиц для формирования выборочной совокупности представлены на схеме (рисунок 6). В случае, когда совокупность характеризуется количественным признаком, основной характеристикой выборочного наблюдения будет средний размер признака: Для характеристики альтернативного (качественного) признака исчисляют относительную величину – долю: p – по генеральной совокупности, w – по выборке. Конечная цель выборочного наблюдения – распространение полученных по выборке данных на генеральную совокупность. Это происходит с помощью предельных ошибок ∆ x и ∆ w:
        
Рисунок 6 - Виды, способы и методы отбора единиц в выборочную совокупность
Формулы определения предельных ошибок зависят от способа отбора единиц в выборку. Таблица 27 - Предельная ошибка выборки для различных способов отбора
Условные обозначения, принятые в формулах: t - коэффициент доверия; σ2 - дисперсия признака в выборочной совокупности;
r - число отобранных серий; R - число серий в генеральной совокупности; n - число отобранных единиц; N - число единиц в генеральной совокупности. Репрезентативность выборочных характеристик в значительной мере зависит от численности выборки. Математическая статистика разработала следующие формулы для определения необходимой численности выборки.
Таблица 28 - Необходимый объем выборки для различных способов формирования выборочной совокупности
Контрольные вопросы: 1.Понятие выборочного наблюдения. 2.Условия применения выборочного наблюдения. 3.Обобщающие характеристики генеральной и выборочной. 4.Виды отбора единиц в выборочную совокупность. 5.Способы отбора единиц в выборочную совокупность 6.Методы отбора единиц в выборочную совокупность. 7.Характеристика случайного отбора. 8. Характеристика механического отбора. 9. Характеристика типического отбора. 10.Характеристика серийного отбора. 11.Ошибки выборочного наблюдения. 12.Определение ошибок при случайном и механическом отборе. 13.Определение ошибок при типическом отборе. 14.Определение ошибок при серийном отборе. 15.Определение численности случайной и механической выборки. 16.Определение численности типической выборки. 17.Определение численности серийной выборки. 18.Понятие малой выборки, сфера ее применения.
Задание 1 При проверке веса импортируемого груза на таможне методом случайной повторной выборки было отобрано 1240 изделий. Средний вес изделия по результатам исследования составил 3,5 кг. Значение дисперсии составило 81. Необходимо: 1) с вероятностью 0,954 определить пределы, в которых находится средний вес изделия в генеральной совокупности; 2) как изменятся пределы, в которых находится средняя по генеральной совокупности, если вероятность будет равна 0,997?
Задание 2 В цеху работает 2450 ткачей. Для определения среднего объема производства ткани в час была организована 4%-ная случайная бесповторная выборка ткачей. По ее результатам было получено следующее распределение ткачей по объему производства ткани в час:
Таблица 29 – Результаты исследования среднего выпуска продукции
С вероятностью 0,95 найдите пределы, в которых будет находиться средний объем производства ткани в генеральной совокупности.
Задание 3 С целью определения среднего удоя молока в хозяйстве с численностью доярок 146 человек в августе 2007 года была произведена 30%-ная механическая выборка. По результатам наблюдения оказалось, что у 3% исследованных фактические надои превышали 25 литров в день. С вероятностью 0,997 установите пределы, в которых находится генеральная доля доярок с удоем молока более 25 литров в день. Каковы будут результаты, если точность расчетов установить равной 0,683?
Задание 4 В партии товара, состоящей из 150 ящиков, проводилось выборочное обследование качества (доли бракованных изделий) на основе отбора серий (ящиков). Выборочные средние по ящикам составили соответственно 3%, 1,05%, 2,01%, 4,0%, 0,6%, 1,9%. С вероятностью 0,683 найдите пределы доли бракованного товара во всей партии. Задание 5 В 100 туристических агентствах города предполагается провести исследование среднего количества реализованных путевок методом механического отбора. Какова должна быть численность выборки, чтобы с вероятностью 0,954 ошибка не превышала 4 путевок, если по данным предварительных расчетов среднеквадратическое отклонение составляет 24?
Задание 6 Для определения доли студентов дневной формы обучения со средним баллом более 9 предполагается организовать типическую выборку пропорционально численности студентов различных курсов с механическим отбором внутри групп. Общее число студентов университета составляет 4390 человек, в. том числе: - студентов 1 курса – 1264 человека; - студентов 2 курса - 912 человек; - студентов 3 курса – 840 человек; - студентов 4 курса – 688 человек; - студентов 5 курса – 686. На основании предыдущих обследований известно, что средняя из внутригрупповых дисперсий составляет 2500. Определите необходимый объем выборки при вероятности 0,997 и ошибке 3%.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 468; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |

 или
или  ;
; или
или  ;
; или
или  ;
; ;
; ;
; .
. ,
,


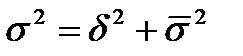
 ,
, ,
,
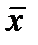 - по генеральной совокупности;
- по генеральной совокупности; 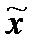 - по выборке.
- по выборке. ,
, .
.





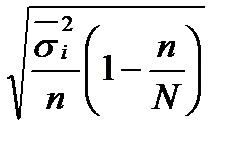





 - межсерийная дисперсия;
- межсерийная дисперсия;