Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение типовых задач к теме 1.7.: Методы изучения взаимосвязи социально-экономических явлений.Содержание книги
Поиск на нашем сайте
Задача №1. Экспертами оценивались вкусовые качества вин. Суммарные оценки получены следующие.
Согласуется ли оценка вина с его ценой? Проверим эту гипотезу методом ранговой корреляции Спирмена и коэффициентом Фехнера. Решение: Оценку тесноты связи с помощью коэффициента Спирмена и Фехнера рассчитываем в табличной форме
Коэффициент Спирмена
Следовательно, связь прямая и тесная. Для определения коэффициента Фехнера рассчитаем среднее значение цены
и среднее значение оценки
x-
Следовательно, связь прямая и существенная. Задача №2. На основании следующих условных данных необходимо исследовать связь между успеваемостью студентов - заочников одного из вузов и их работой по специальности с помощью коэффициентов ассоциации и контингенции.
Решение: Коэффициент ассоциации
Связь подтверждается т.к. Кa≥0,5 Коэффициент контингенции
Связь подтверждается т.к. Кk=0,3 Задача № 3. С помощью коэффициентов взаимной сопряженности Пирсона и Чупрова необходимо исследовать связь между себестоимостью продукции производительностью труда на основании нижеследующих данных:
Решение: Коэффициент Пирсона:
А Следовательно, связь средняя. Коэффициент Чупрова
Следовательно связь средняя. Задача № 4. По результатам экспертной оценки степени влияния факторов на уровень производительности труда факторам были присвоены следующие ранги
Определить с помощью коэффициента корреляции рангов Кендалла насколько точно результаты экспертной оценки предугадали действительную степень влияния факторов на уровень производительности труда. Решение: Коэффициент корреляции рангов Кэндапла:
т.к. S=P+Q определяем Р=81 это количество чисел, находящихся после каждого ю элементов последовательности рангов переменной у, имеющих величину ранга, превышающую ранг рассматриваемого элемента т.е.числу у=3 соответствует 12 чисел (7,6,8,4,5,13,14,9,12,11,15,10), второму значению у=2 соответствует тоже12 чисел (7,6,8,4,5,13,14,9,12,11,15,10), третьему значению у=7 соответствует 8 чисел (8,13,14,9,12,11,15,10)и так далее. Отсюда P=12+12+8+8+10+7+8+7+2+1+4+1+1=81. Далее определяем Q =24,т.е. количество чисел после каждого из членов последовательности рангов переменной у, имеющих ранг меньше, чем у рассматриваемого. Эти числа берутся со знаком минус. Так у=3 соответствует 2 числа (-2,-1), для у=2 соответствует 1 число (-1), для у=7 соответствует 4 числа (-6,-1,-4,-5) и так далее. Отсюда Q=2-1 -4-3-0-2-0-0-4-4-0-2-1-1=-24 Следовательно степень влияния отобранных факторов на производительность труда экспертами была существенной. Задача №5. По данным о стоимости основных производственных фондов и объеме товарной продукции определите уравнение связи и тесноту связи:
Связь предполагается линейная, уравнение прямой ¯yx=a0+a1x Решаем систему уравнений методом наименьших квадратов либо по формулам (1.7.6) и (1.7.7):
Коэффициент регрессии а1 свидетельствует о том, что при увеличении объема основных фондов на 1млн. руб.количество товарной продукции увеличится на 5,6 млн.руб. Тесноту связи определяем по линейному коэффициенту корреляции
Следовательно, связь прямая и очень тесная. Задача № 6.
Произведем выравнивание по параболе второго порядка: Решаем систему нормальных уравнений:
Решение этой системы уравнений методом наименьших квадратов или по формулам (1.7.6) и (1.7.7) дает следующие значения параметров: a0=5,086 a1=27,511 a2=-6,927
Задача № 7. Для изучения тесноты связи между выпуском продукции на 1 завод и оснащенностью заводов основными фондами определите по следующим данным эмпирическое корреляционное отношение:
Результат группировки данных по стоимости основных фондов представлен в нижеследующей таблице
В данной задаче факторный признак оснащенность основными фондами (х), А результативный - выпуск продукции на 1 завод (у). Решение: Корреляционное отношение определяется по формуле
Общая средняя признака у,
Составим расчетную таблицу:
Определяем межгрупповую дисперсию Общая дисперсия определяется по исходным данным:
Теперь можно вычислить корреляционное отношение:
Это означает, что связь между стоимостью основных фондов и выпуском продукции тесная.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 366; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.28.160 (0.009 с.) |



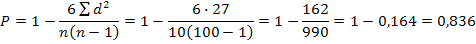

 Тогда количество совпадений знаков отклонений
Тогда количество совпадений знаков отклонений

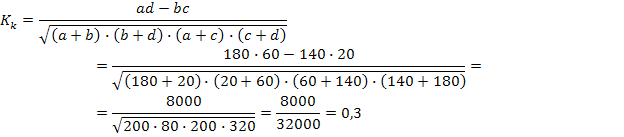





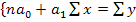 a0=13,8 ¯yx=13,8+5,6x
a0=13,8 ¯yx=13,8+5,6x a1=5,6
a1=5,6

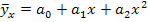


 30a+32,90a1+38,484a2=781,1
30a+32,90a1+38,484a2=781,1 32,90a0+38,484a1+47,0762a2=899,95
32,90a0+38,484a1+47,0762a2=899,95 =5,086+27,511x-6,927x2
=5,086+27,511x-6,927x2 где общая дисперсия признака y,
где общая дисперсия признака y, 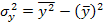 , а межгрупповая дисперсия
, а межгрупповая дисперсия  ,
,  вычисляем по данным группировки в вышеизложенной таблице,
вычисляем по данным группировки в вышеизложенной таблице,  ,
,  ,
, 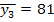 ,
, 
 заводам.
заводам.




 где
где