
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сезонные колебания. Индексы сезонных колебаний и сезонная волна.Содержание книги
Поиск на нашем сайте
При сравнении квартальных и месячных данных многих социально-экономических явлений часто обнаруживаются периодические колебания, возникающие под влиянием смены времен года.
В статистике существует ряд методов изучения и измерения сезонных колебаний. Самый простой заключается в построении специальных показателей, которые называются индексами сезонности Is. Совокупности этих показателей отражает сезонную волну.
Y- среднемесячный уровень для всего ряда. 41.
Индексы. Классификация индексов в статистике по степени охвата явления, базе сравнения, форме построения, объекту исследования, составу явления, периоду исчисления. Слово «индекс» имеет несколько значений: -показатель,
-указатель, -опись и т.д.
По степени охватта явления индексы бывают индивидуальные и общие. По базе сравнения индексы подразделяются на: -динамические -территориальные По виду весов индексы бывают с постоянными и переменными весами. В зависимости от формы построения индексы бывают агрегатные и средние. По характеру объема исследования общие индексы подразделяются на: -индексы количественных -индексы качественных показателей. По объекту исследования индексы бывают: -производительности труда -себестоимости -цены -физического объема продукции и т.д. По составу явления индексы постоянного и переменного состава. С помощью индексов решаются следующие задачи: 1. Измерение динамики, социально-экономического явления за 2 и более периода времени. 2. Измерение динамики среднего экономического показателя. 3. Измерение соотношения показателей по разным регионам.
42.
Индивидуальные и общие индексы. Агрегатный индекс. Индивидуальные индексы получают в результате сравнения однотоварных явлений. Индивидуальные индексы показывают во сколько раз или процентов показатель у единицы наблюдения за текущий период изменился по сравнению с показателем за базисный период. Различают 4 индивидуальных индекса: 1. индекс цен показывает как изменилась цена в текущем периоде по сравнению с базисным. P1- цена единицы товара в текущем периоде P0- цена единицы товара в базисном периоде 2. индекс физического объема показывает как изменился объем продукции в текущем периоде по сравнению с базисным q1- кол-во проданного или произведеннго товара в текущем периоде q0-кол-во проданного или произведенного товара в базисном периоде 3. индекс себестоимости показывает, как изменилась себестоимость единицы продукции в текущем периоде по сравнению с базисным. Z1- себестоимость единицы продукции в текущем периоде Z0- себестоимость единицы продукции в базисном периоде 4. индекс производительности труда показывает, как изменилась производительность труда одного работающего в текущем периоде по сравнению с базисным периодом t0- трудоемкость обного работающего за базисный период t1- трудоемкость одного работающего за текущий период Агрегатные индексы являются формой общих индексов. Их рассчитывают, когда известны данные за базисный и текущий периоды по группе товаров. Существует 4 основных формулы агрегатных индексов 1. индекс цен P- цена единицы товара q- кол-во проданного товара P*q- выручка (товарооборот)
Автором этой формулы является немецкий статистик Г. Пааше.
Э. Ласпейрес
До 90-х гг. XX века в России использовали индекс цен Пааше. С 1991 года Госкомстат считает индекс цен по формуле Ласпейреса.
2. индекс физического объема 3. индекс себестоимости 4. индекс производительности труда τ- трудоемкость единицы продукции q- кол-во произведенной продукции t*q- затраты времени на производство С помощью агрегатных индексов можно определять сумму экономического эффекта, как разницу между числителем и знаменателем общего индекса. Если сумма эффекта >0, то наблюдается экономия денежных средств, либо времени Если<0, то дополнительные затраты. Сумма эффекта
Средние индексы. Средние арифметические индексы. Средние арифметические индексы используются, когда известны данные только за базисный период и изменение показателя в текущем периоде, т.е. индивидуальные индексы. Рассмотрим преобразование агрегатного индекса в средний арифметический на примере индекса физического объема.
Неизвестно q1, поэтому выразим его через индивидуальный индекс Подставим получившееся выражение в формулу агрегатного индекса
Среднегармонические индексы. Среднегармонические индексы используются, когда известны данные только за текущий период и изменение показателей по сравнению с базисным периодом,т.е. индивидуальный индекс.
Подставим получившееся выражение в формулу общего индекса
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 580; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.176.191 (0.006 с.) |

 В статистике периодические колебания, которые имеют определенный и постоянный период, равный годовому промежутку, носят название «сезоные колебания» или «сезонные волны», а динамический ряд в этом случае называют сезонным рядом динамики.
В статистике периодические колебания, которые имеют определенный и постоянный период, равный годовому промежутку, носят название «сезоные колебания» или «сезонные волны», а динамический ряд в этом случае называют сезонным рядом динамики. Индексами сезонности являются % отношения фактических (эмпирических) внутригрупповых уровней к теоритическим (расчетным) уровням, выступающим в качестве базы сравнения.
Индексами сезонности являются % отношения фактических (эмпирических) внутригрупповых уровней к теоритическим (расчетным) уровням, выступающим в качестве базы сравнения.
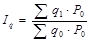

 Это слово, как понятие, используют в математике, экономике и др. науках. В статистике под индексом понимается относительный показатель, который выражает соотношение величин какого-либо явления во времени, в пространстве.
Это слово, как понятие, используют в математике, экономике и др. науках. В статистике под индексом понимается относительный показатель, который выражает соотношение величин какого-либо явления во времени, в пространстве.









